Chainer を使って、深層学習(deep learning)の基本的な考えを学びます。
Chainerの基本パーツ
chainer.Variable
Chainer では、変数を Variable というクラスとして記述します。
import numpy as np
from chainer import Variable
x1 = Variable(np.array([0.12]).astype(np.float32))
x2 = Variable(np.array([0.34]).astype(np.float32))
x3 = Variable(np.array([0.56]).astype(np.float32))
次のような演算で「順方向の計算」を行います。深層学習では、これらの係数(下記の0.5, 0.3, 0.2など)を「勾配」と呼び、最適な勾配の値を求めることを計算の目的とします。
z = 0.5 * x1 + 0.3 * x2 + 0.2 * x3
演算結果もまた Variable クラスのオブジェクトです。
z
variable([0.274])
.data という属性を用いると、データの中身である numpy.ndarray オブジェクトを参照できます。
z.data
array([0.274], dtype=float32)
次のようにして「逆方向の計算」を行います。逆方向の計算の目的は、順方向の計算結果の誤差を「逆伝播」して、上に述べた「係数」を微調整することです。
z.backward()
逆方向の計算によって、各変数の係数を微調整する時に必要な「微分値」が得られます。
x1.grad, x2.grad, x3.grad
(array([0.5], dtype=float32),
array([0.3], dtype=float32),
array([0.2], dtype=float32))
これまで変数は1次元でしたが、以下のように、多次元配列を用いることもできます。
x1 = Variable(np.array([0.12, 0.21]).astype(np.float32))
x2 = Variable(np.array([0.34, 0.43]).astype(np.float32))
x3 = Variable(np.array([0.56, 0.65]).astype(np.float32))
z = 0.5 * x1 + 0.3 * x2 + 0.2 * x3
z
variable([0.274, 0.364])
変数が多次元の場合は、「逆方向の計算」をする前に、関数の傾きの次元をあらかじめ教えておく必要があります。
z.grad = np.ones(2, dtype=np.float32)
z.backward()
x1.grad, x2.grad, x3.grad
(array([0.5, 0.5], dtype=float32),
array([0.3, 0.3], dtype=float32),
array([0.2, 0.2], dtype=float32))
chainer.links.Linear
Chainer では、深層学習を行うニューラルネットワーク(NN)において、ある層から次の層へとデータを受け渡す際に用いる線形変換関数を chainer.links.Linear として提供しています。線形変換は
$y = Wx + b$
として表されます。chainer.links.Linearを用いる前に、numpy で線形変換を表現してみましょう。
import numpy as np
W = np.array([[ 5, 1, -2 ],
[ 3, -5, -1 ]], dtype=np.float32)
b = np.array([2, -3], dtype=np.float32)
入力データが1つだけ(3変数から成るデータが1つだけ)の場合は、次のように計算できます。
x = np.array([0, 1, 2])
y = x.dot(W.T) + b
y
array([ -1., -10.])
入力データが5つ(3変数から成るデータが5つ)の場合は、次のように計算できます。このように、データが多数あっても並列で計算できるのが行列計算の強みです。
x = np.array(range(15)).astype(np.float32).reshape(5, 3)
x
array([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.],
[ 9., 10., 11.],
[12., 13., 14.]], dtype=float32)
y = x.dot(W.T) + b
y
array([[ -1., -10.],
[ 11., -19.],
[ 23., -28.],
[ 35., -37.],
[ 47., -46.]], dtype=float32)
上記と同じような計算を chainer.links.Linear で実現できます。
import chainer.links as L
h = L.Linear(3,2) # 3次元ベクトルを入力し、2次元のベクトルを出力する線形作用関数 y = Wx + b
h.W.data # デフォルトでは乱数が入る
array([[ 0.5469049 , -0.35929427, -0.9921321 ],
[ 1.4973897 , 0.620568 , 0.78245926]], dtype=float32)
h.b.data # デフォルトでは0ベクトルが入る
array([0., 0.], dtype=float32)
x = Variable(np.array(range(15)).astype(np.float32).reshape(5, 3))
x.data # Variable.data は Numpy の配列オブジェクト
array([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.],
[ 9., 10., 11.],
[12., 13., 14.]], dtype=float32)
y = h(x)
y.data
array([[ -2.3435585, 2.1854866],
[ -4.757123 , 10.886737 ],
[ -7.170687 , 19.587988 ],
[ -9.584251 , 28.289238 ],
[-11.997816 , 36.990486 ]], dtype=float32)
x.data.dot(h.W.data.T) + h.b.data # 検算
array([[ -2.3435585, 2.1854866],
[ -4.757123 , 10.886737 ],
[ -7.170687 , 19.587988 ],
[ -9.584251 , 28.289238 ],
[-11.997816 , 36.990486 ]], dtype=float32)
chainer.functions
Chainer では、Variable クラスのオブジェクトを引数とする各種関数を chainer.functions で提供しています。代表例は平均平方根誤差 chainer.functions.mean_squared_error です。
import chainer.functions as F
y_pred = Variable(np.array([0.1, 0.2, 0.3]).astype(np.float32))
y_real = Variable(np.array([0.2, 0.1, 0.3]).astype(np.float32))
loss = F.mean_squared_error(y_pred, y_real)
loss
variable(0.00666667)
線形重回帰 Multiple Linear Regresion (MLR)
それでは、Chainer の練習として、線形重回帰をしてみましょう。取り扱うデータとして、機械学習分野でよく用いられる Iris (アヤメ)のデータを取り扱います。
アヤメのデータ
import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
data = iris.data.astype(np.float32)
X = data[:, :3] # アヤメの計測データのうち、最初の3つを説明変数とします。
Y = data[:, 3].reshape(len(data), 1) # 最後の1つを目的変数とします。
# 奇数番目のデータを教師データ、偶数番目のデータをテストデータとします。
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数(教師データ)
X_test = X[index[index % 2 == 0], :] # 説明変数(テストデータ)
Y_train = Y[index[index % 2 != 0], :] # 目的変数(教師データ)
Y_test = Y[index[index % 2 == 0], :] # 目的変数(テストデータ)
chainer.Sequential
chainer.Sequential で、ニューラルネットワークの構造を定義します。
import chainer.links as L
from chainer import Sequential
n_input = 3 # 入力データは3変数
n_output = 1 # 出力データは1変数
mlr = Sequential( # ニューラルネットワークを定義
L.Linear(n_input, n_output) # 1層だけから成るニューラルネットワーク
)
最初に定義した時は、係数(勾配)としてデタラメな数字が入っています。
mlr[0].W.data, mlr[0].b.data # このようにして係数を参照できます
(array([[ 0.8395325 , 0.26789278, -0.4547218 ]], dtype=float32),
array([0.], dtype=float32))
次のようにして「順方向の計算」ができます。ただし、係数がランダムな初期値のままなので、得られる予測値もデタラメです。
Y_pred = mlr(X_test) # 順方向の計算
Y_pred
variable([[4.5826297],
[4.211921 ],
[4.525466 ],
[4.136074 ],
[3.8342214],
[4.842596 ],
[4.196824 ],
[5.3951936],
[4.9871187],
[5.0303006],
[4.6712837],
[4.3715415],
[4.07662 ],
[4.380943 ],
[4.6397934],
[4.132669 ],
[4.7818465],
[4.2620945],
[4.9639153],
[3.9064832],
[4.544149 ],
[3.9600616],
[4.435637 ],
[4.5720534],
[4.758643 ],
[4.596792 ],
[4.395105 ],
[4.11534 ],
[4.0359087],
[4.226083 ],
[3.1419218],
[3.807672 ],
[3.841272 ],
[3.458812 ],
[3.7482173],
[3.6278338],
[3.73065 ],
[4.1945934],
[4.276256 ],
[3.7678359],
[3.5324283],
[3.8191838],
[3.2909057],
[4.318143 ],
[3.6407008],
[3.313174 ],
[3.7469225],
[3.5148606],
[3.6523929],
[3.5871825],
[3.44477 ],
[4.0815 ],
[3.623253 ],
[2.7371933],
[3.657213 ],
[3.995137 ],
[4.01153 ],
[3.300307 ],
[3.7596698],
[4.02334 ],
[4.058117 ],
[4.1678634],
[3.9169993],
[3.7725363],
[3.5766659],
[4.188837 ],
[3.5766659],
[3.2712274],
[3.653448 ],
[3.6582088],
[3.908893 ],
[3.2735178],
[3.9169993],
[3.6851778],
[3.660439 ]])
chainer.optimizers
chainer.optimizers では、様々な最適化手法が提供されています。その中の一つが 確率的勾配降下法 stochastic gradient descent (SGD) です。
from chainer import optimizers
optimizer = optimizers.SGD(lr=0.01) # 最適化手法として SGD を選択
optimizer.setup(mlr) # 定義したネットワークをセットアップ
<chainer.optimizers.sgd.SGD at 0x7f2e090bb7f0>
先ほど求めた予測値 Y_pred を、実際の観測値 Y_train と比較し、その平均平方根誤差 MSE を得ます。誤差の定義として他にもいくつか選択できます。深層学習ではこれらの誤差を「損失(loss)」と呼び、損失を求める関数を「損失関数」と呼びます。深層学習では、この損失を最小化することを目指します。
import chainer.functions as F
loss = F.mean_squared_error(Y_pred, Y_train)
loss
variable(9.235707)
次のようにして、逆方向の計算を行い、誤差が少なく成るように勾配を更新します。
mlr.cleargrads() # 勾配の初期化
loss.backward() # 逆方向の計算
optimizer.update() # 勾配の更新
勾配の値が変化したことを確認してみましょう。
mlr[0].W.data, mlr[0].b.data
(array([[ 0.51864076, 0.08801924, -0.63399327]], dtype=float32),
array([-0.05653327], dtype=float32))
以上の計算を、lossが収束するまで繰り返します。
%time
for i in range(50):
Y_pred = mlr(X_test) # 順方向の計算
loss = F.mean_squared_error(Y_pred, Y_train) # 誤差の計算
mlr.cleargrads() # 勾配の初期化
loss.backward() # 逆方向の計算
optimizer.update() # 勾配の更新
CPU times: user 3 µs, sys: 1 µs, total: 4 µs
Wall time: 8.11 µs
loss が減ったことを確認しましょう。
loss
variable(0.15386367)
最初から最後まで
以上の流れをまとめると、次のようになります。
%time
import numpy as np
import chainer.links as L
import chainer.functions as F
from chainer import Sequential
from chainer import optimizers
from sklearn import datasets
iris = datasets.load_iris()
data = iris.data.astype(np.float32)
X = data[:, :3]
Y = data[:, 3].reshape(len(data), 1)
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :]
X_test = X[index[index % 2 == 0], :]
Y_train = Y[index[index % 2 != 0], :]
Y_test = Y[index[index % 2 == 0], :]
n_input = 3
n_output = 1
mlr = Sequential(
L.Linear(n_input, n_output)
)
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(mlr)
loss_history = []
for i in range(100):
Y_pred = mlr(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
loss_history.append(np.mean(loss.data))
mlr.cleargrads()
loss.backward()
optimizer.update()
CPU times: user 2 µs, sys: 1e+03 ns, total: 3 µs
Wall time: 4.77 µs
loss
variable(0.05272739)
mlr[0].W.data, mlr[0].b.data
(array([[ 0.11841334, -0.2642416 , 0.324636 ]], dtype=float32),
array([0.08475045], dtype=float32))
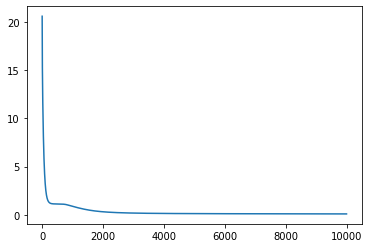
繰り返し計算ごとに loss の値を記録していたので、それを図示して、lossが収束したかどうか確認します。
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)
[<matplotlib.lines.Line2D at 0x7f2e08bfcbe0>]
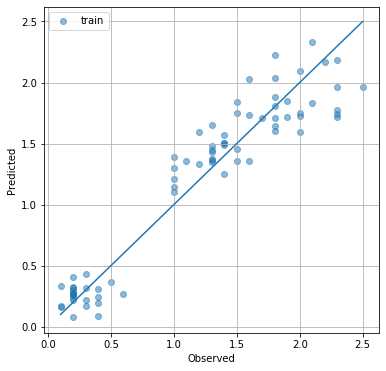
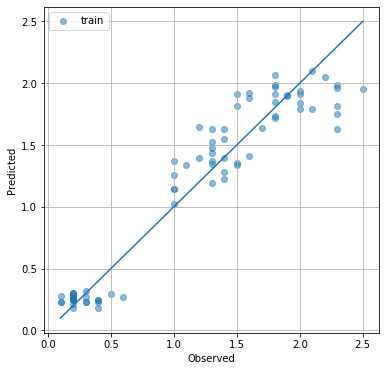
収束したようですね。では、予測値と実測値を比較した y-y プロットを眺めてみましょう。対角線に近いほど、良い予測だと言えます。
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.scatter(Y_train.flatten(), mlr(X_train).data.flatten(), alpha=0.5, label='train')
plt.plot([min(Y), max(Y)], [min(Y), max(Y)])
plt.grid()
plt.legend()
plt.xlabel('Observed')
plt.ylabel('Predicted')
plt.show()
ロジスティック回帰 Logistic Regression (LR)
次は、シグモイド関数(ロジスティック関数)に回帰する手法であり、分類手法としても用いられるロジスティック回帰を行ってみましょう。
アヤメのデータ
今度は、アヤメの4つの計測データを説明変数に、アヤメの品種(3種)を目的変数にします。
import numpy as np
from sklearn import datasets
iris = datasets.load_iris() # アヤメのデータの読み込み
X = iris.data.astype(np.float32) # 4変数を説明変数に
Y = iris.target # アヤメの品種(3種)を目的変数に
# アヤメの品種を one-hot vector に変換します。
Y_ohv = np.zeros(3 * Y.size).reshape(Y.size, 3).astype(np.float32)
for i in range(Y.size):
Y_ohv[i, Y[i]] = 1.0 # one-hot vector
# 奇数番目のデータを教師データ、偶数番目のデータをテストデータとします。
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :] # 説明変数(教師データ)
X_test = X[index[index % 2 == 0], :] # 説明変数(テストデータ)
Y_train = Y_ohv[index[index % 2 != 0], :] # 目的変数の one-hot vector (教師データ)
Y_test = Y_ohv[index[index % 2 == 0], :] # 目的変数の one-hot vector (テストデータ)
Y_ans_train = Y[index[index % 2 != 0]] # 目的変数(教師データ)
Y_ans_test = Y[index[index % 2 == 0]] # 目的変数(テストデータ)
ニューラルネットワークの定義
from chainer import Sequential
import chainer.links as L
import chainer.functions as F
n_input = 4 # 入力は4変数
n_output = 3 # 出力は3変数
lr = Sequential(
L.Linear(n_input, n_output), # 線形変換
F.sigmoid, # シグモイド関数
F.softmax # 和が1となる正の実数に変換するソフトマックス関数
)
最適化
from chainer import optimizers
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(lr)
<chainer.optimizers.sgd.SGD at 0x7f2e0878b7b8>
Y_pred = lr(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
loss
variable(0.21429048)
lr.cleargrads()
loss.backward()
optimizer.update()
Y_pred = lr(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
loss
variable(0.21422786)
%time
for i in range(50):
Y_pred = lr(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
lr.cleargrads()
loss.backward()
optimizer.update()
CPU times: user 7 µs, sys: 1 µs, total: 8 µs
Wall time: 28.1 µs
loss
variable(0.21126282)
最初から最後まで
以上の流れをまとめると、次のようになります。
%time
import numpy as np
import chainer.links as L
import chainer.functions as F
from chainer import Sequential
from chainer import optimizers
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data.astype(np.float32)
Y = iris.target
Y_ohv = np.zeros(3 * Y.size).reshape(Y.size, 3).astype(np.float32)
for i in range(Y.size):
Y_ohv[i, Y[i]] = 1.0 # one-hot vector
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :]
X_test = X[index[index % 2 == 0], :]
Y_train = Y_ohv[index[index % 2 != 0], :]
Y_test = Y_ohv[index[index % 2 == 0], :]
Y_ans_train = Y[index[index % 2 != 0]]
Y_ans_test = Y[index[index % 2 == 0]]
n_input = 4
n_output = 3
lr = Sequential(
L.Linear(n_input, n_output),
F.sigmoid,
F.softmax
)
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(lr)
loss_history = []
for i in range(100000):
Y_pred = lr(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
loss_history.append(np.mean(loss.data))
lr.cleargrads()
loss.backward()
optimizer.update()
CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 5.01 µs
loss
variable(0.14579579)
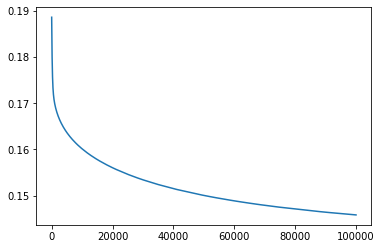
繰り返し計算ごとに loss の値を記録していたので、それを図示して、lossが収束したかどうか確認します。
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)
[<matplotlib.lines.Line2D at 0x7f2e06445080>]
lr[0].W.data, lr[0].b.data
(array([[ 0.7060194 , 1.5789627 , -2.7305322 , -1.5006719 ],
[-0.6907905 , -0.43505952, -0.78199637, -0.06515903],
[-1.7571408 , -2.1365883 , 2.8683107 , 2.772224 ]],
dtype=float32),
array([ 0.2556363 , -0.15823539, -0.9368208 ], dtype=float32))
最後の層を、和が1となる正の実数に変換するソフトマックス関数にしたので、出力は「その品種とみなせる確率」とみなせます。その確率が最大値になる品種が「予測された品種」であるとしたときの、正答率を求めましょう。
Y_pred = lr(X_train)
nrow, ncol = Y_pred.data.shape
count = 0
for i in range(nrow):
cls = np.argmax(Y_pred.data[i, :])
if cls == Y_ans_train[i]:
count += 1
print(count, " / ", nrow, " = ", count / nrow)
50 / 75 = 0.6666666666666666
多層パーセプトロン Multi-Layer Perceptron (MLP)
これまで、Chainer を用いた線形重回帰とロジスティック回帰モデルを作成してみました。同じような要領で、層を厚くしていくと「深層学習」になります。深層学習の中で最も単純なモデルが多層パーセプトロンです。
MLP による分類
%time
import numpy as np
from chainer import Sequential
from chainer import optimizers
import chainer.links as L
import chainer.functions as F
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data.astype(np.float32)
Y = iris.target
Y_ohv = np.zeros(3 * Y.size).reshape(Y.size, 3).astype(np.float32)
for i in range(Y.size):
Y_ohv[i, Y[i]] = 1.0 # one-hot vector
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :]
X_test = X[index[index % 2 == 0], :]
Y_train = Y_ohv[index[index % 2 != 0], :]
Y_test = Y_ohv[index[index % 2 == 0], :]
Y_ans_train = Y[index[index % 2 != 0]]
Y_ans_test = Y[index[index % 2 == 0]]
n_input = 4
n_hidden = 6
n_output = 3
mlp = Sequential(
L.Linear(n_input, n_hidden),
F.sigmoid,
L.Linear(n_hidden, n_output),
F.softmax
)
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(mlp)
loss_history = []
for i in range(100000):
Y_pred = mlp(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
loss_history.append(np.mean(loss.data))
mlp.cleargrads()
loss.backward()
optimizer.update()
CPU times: user 3 µs, sys: 0 ns, total: 3 µs
Wall time: 5.48 µs
loss
variable(0.01375966)
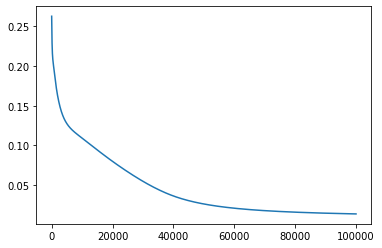
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)
[<matplotlib.lines.Line2D at 0x7f2e08746fd0>]
Y_pred = mlp(X_train)
nrow, ncol = Y_pred.data.shape
count = 0
for i in range(nrow):
cls = np.argmax(Y_pred.data[i, :])
if cls == Y_ans_train[i]:
count += 1
print(count, " / ", nrow, " = ", count / nrow)
74 / 75 = 0.9866666666666667
MLP による回帰
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
data = iris.data.astype(np.float32)
X = data[:, :3]
Y = data[:, 3].reshape(len(data), 1)
index = np.arange(Y.size)
X_train = X[index[index % 2 != 0], :]
X_test = X[index[index % 2 == 0], :]
Y_train = Y[index[index % 2 != 0], :]
Y_test = Y[index[index % 2 == 0], :]
%time
import numpy as np
from chainer import Sequential
from chainer import optimizers
import chainer.links as L
import chainer.functions as F
n_input = 3
n_hidden = 6
n_output = 1
mlpr = Sequential(
L.Linear(n_input, n_hidden),
F.sigmoid,
L.Linear(n_hidden, n_output)
)
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(mlpr)
loss_history = []
for i in range(10000):
Y_pred = mlpr(X_train)
loss = F.mean_squared_error(Y_pred, Y_train)
loss_history.append(np.mean(loss.data))
mlpr.cleargrads()
loss.backward()
optimizer.update()
CPU times: user 4 µs, sys: 0 ns, total: 4 µs
Wall time: 8.82 µs
loss
variable(0.04921096)
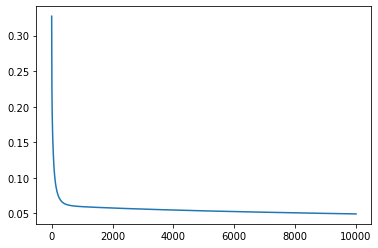
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)
[<matplotlib.lines.Line2D at 0x7f2e064200f0>]
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(6,6))
plt.scatter(Y_train.flatten(), mlpr(X_train).data.flatten(), alpha=0.5, label='train')
plt.plot([min(Y), max(Y)], [min(Y), max(Y)])
plt.grid()
plt.legend()
plt.xlabel('Observed')
plt.ylabel('Predicted')
plt.show()
オートエンコーダー AutoEncoder (AE)
オートエンコーダーは、自分自身に回帰するニューラルネットワークです。入力層から中間層への変換器はエンコーダー encoder、中間層から出力層への変換器はデコーダー decoder と呼ばれます。中間層のニューロン数を入力データより少なくすることで「次元縮約」(次元削減)できます。
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data.astype(np.float32)
%time
import numpy as np
from chainer import Sequential
from chainer import optimizers
import chainer.links as L
import chainer.functions as F
n_input = 4
n_hidden = 2
n_output = 4
ae = Sequential(
L.Linear(n_input, n_hidden),
F.sigmoid,
L.Linear(n_hidden, n_output),
)
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(ae)
loss_history = []
for i in range(10000):
X_pred = ae(X)
loss = F.mean_squared_error(X_pred, X)
loss_history.append(np.mean(loss.data))
ae.cleargrads()
loss.backward()
optimizer.update()
CPU times: user 5 µs, sys: 0 ns, total: 5 µs
Wall time: 9.54 µs
loss
variable(0.09372737)
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(loss_history)
[<matplotlib.lines.Line2D at 0x7f2e06699a58>]
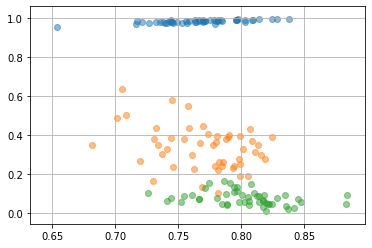
中間層に投影されたデータを見る
latent = F.sigmoid(ae[0](X))
%matplotlib inline
import matplotlib.pyplot as plt
plt.scatter(latent.data[0:50, 0], latent.data[0:50, 1], alpha=0.5)
plt.scatter(latent.data[50:100, 0], latent.data[50:100, 1], alpha=0.5)
plt.scatter(latent.data[100:150, 0], latent.data[100:150, 1], alpha=0.5)
plt.grid()