皆さんこんにちは。今日も引き続きChatGPT先生をお迎えして、「ChatGPTとPythonで学ぶ カーネルk-means クラスタリング」というテーマで雑談したいと思います。それではChatGPT先生、よろしくお願いします。
assistant:
もちろんです、よろしくお願いします。
カーネルk-meansクラスタリングは、データのクラスタリングアルゴリズムの一つで、通常のk-meansクラスタリングが直線的な分離しかできないのに対し、カーネルk-meansは非線形なデータ分離も可能です。そのため、もとのデータの特性を維持しつつ、より柔軟にクラスタリングを行うことができます。
Pythonによるカーネルk-meansクラスタリングのコードを一緒に見てみましょう。なお、ここではscikit-learnという機械学習のライブラリを用いることを前提としましょう。カーネルk-meansそのものは直接サポートされていませんが、ここではKernelPCAを組み合わせて、それを実現する方法を紹介します。
import numpy as np
from sklearn.datasets import make_circles
from sklearn.cluster import KMeans
from sklearn.decomposition import KernelPCA
# データの生成
X, _ = make_circles(n_samples=400, factor=.3, noise=.05)
# カーネルPCAによる変換
kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
# k-meansクラスタリング
kmeans = KMeans(n_clusters=2).fit(X_kpca)
# クラスタリング結果の出力
print(kmeans.labels_)
[0 0 0 0 0 0 1 0 1 0 1 1 1 1 1 0 1 0 1 1 0 1 0 0 1 0 0 1 0 0 0 0 0 1 0 1 1
0 1 1 0 0 1 1 0 0 0 0 1 1 1 1 1 0 0 1 0 0 0 1 0 0 1 1 1 0 1 1 0 0 1 0 0 0
1 1 0 0 1 1 0 1 1 1 1 0 1 0 1 1 1 1 0 0 0 0 1 0 1 0 1 0 1 1 1 1 0 0 0 0 0
0 0 1 0 1 1 0 1 0 1 0 1 1 1 0 0 0 0 0 0 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1
1 1 0 1 1 1 1 1 1 1 1 1 0 0 0 1 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 1 0 0 1
1 0 0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 1 1 0 0 0 1 1 0 0 0 1 0 1 0 1 0 0 1 0 1
1 1 0 0 0 1 1 1 0 0 1 0 0 0 0 1 1 1 0 1 1 1 1 1 0 1 0 1 0 0 0 1 0 1 1 0 1
1 0 1 1 1 0 1 0 1 0 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 1 1 0 1
1 1 1 0 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 1 1 0 0 0
1 1 0 0 0 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 0 1 0 0 0 0 1 1 1 1 1 0 0 1 1 0 0
0 1 0 1 1 1 1 1 1 1 0 1 0 1 1 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0]
このコードの中で、まずmake_circles関数で円形にデータを生成しています。次に、カーネルPCAによりデータを非線形変換しています。ここでは、rbf(Radial basis function)というカーネルを利用しています。そして、変換されたデータに対してk-meansクラスタリングを行い、その結果を出力しています。
これにより、もとのデータ空間で非線形なクラスタリングを実現できます。ただし、カーネルの選択やパラメータの調整は、具体的なデータやタスクに依存するため、これ自体が重要な問題となります。適切なパラメータ選択には交差検証などの手法がありますが、詳細は割愛します。
以上がカーネルk-meansクラスタリングの基本的な説明と、scikit-learnを用いたPythonでの実装例です。ご質問があればお知らせください。
user:
結果を可視化してください。
assistant:
もちろんです。以下のようにmatplotlibを使ってクラスタリングの結果を可視化しましょう。
import matplotlib.pyplot as plt
# 元のデータの分布
plt.figure(figsize=(6, 3))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1])
plt.title("Original data")
# クラスタリング結果
plt.subplot(122)
plt.scatter(X_kpca[:, 0], X_kpca[:, 1], c=kmeans.labels_)
plt.title("Clustering result")
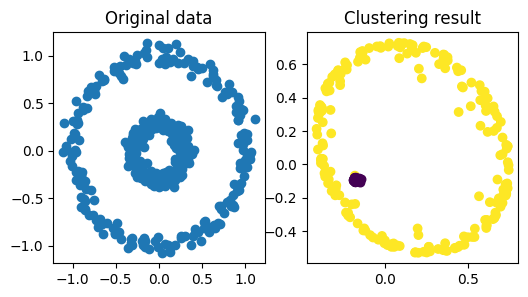
plt.show()
これにより、元のデータの分布とクラスタリングの結果を並べて表示することができます。
左側が元のデータの分布で、右側がクラスタリングの結果です。クラスタリングの結果は、色でクラスタの所属を示しています。カーネルk-meansクラスタリングにより、非線形なクラスタリングができていることがわかります。
user:
オリジナルデータを色分けできませんか?
assistant:
それでは各サンプルの所属クラスタに応じて元データへの色分けを行いましょう。以下のコードブロックがそれに対応します。
plt.figure(figsize=(6, 3))
# オリジナルのデータの分布をクラスタラベルに基づいて色分けして描画
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
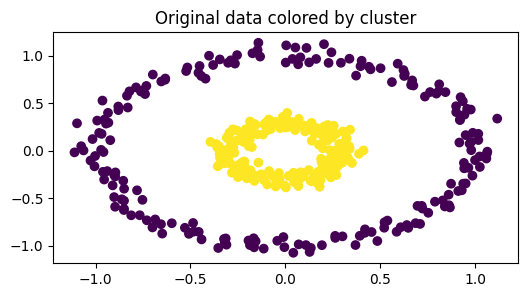
plt.title("Original data colored by cluster")
plt.show()
このコードにより、元のデータについて各サンプルがどのクラスタに所属するか色分けして表示します。
user:
おお、ちゃんとできてますね。kernel k-means を行うために pyclustering や sklearn-extra を教えてもらったことがありますが、scikit-learnだけでできるんですね。
assistant:
はい、その通りです。Pythonには多くのマシンラーニングやデータ分析に便利なライブラリが存在します。pyclusteringやsklearn-extraはその一部であり、これらも非常に有用なツールです。
しかし、scikit-learnだけでも多くの基本的な処理は実現可能で、非線形データのクラスタリングもカーネルPCAとk-meansを組み合わせることで実現できます。特にscikit-learnはその充実したドキュメンテーションや広大なユーザーコミュニティが存在するため、初学者には非常に使いやすいライブラリです。
ただし、より高度な機能や特殊なアルゴリズムを求める場合には、それに特化した他のライブラリを使用すると良いでしょう。全ての道具を切実に理解する必要は無く、どのツールが何を提供し、それが自分のニーズにどのくらい対応しているかを把握し、適切なツールを選ぶ能力が重要です。
user:
kernel k-means を行うために、scikit-learn だけで実装する場合と、pyclusteringやsklearn-extraを使う場合で、何が違うか詳しく教えていただきますか?
assistant:
はい、もちろんです。それぞれについて詳しく説明します。
最初に、 scikit-learn だけでカーネルk-meansを実装する場合、私たちは以下のステップを組み合わせています:
- カーネルPCAを使用して、データを高次元の特徴空間にマッピングします。この変換は非線形で、元の特徴空間で線形分離可能でないクラスタが、新しい空間で線形分離可能になる可能性があります。
- 変換された特徴空間でk-meansクラスタリングを実行します。
しかしこのアプローチにはいくつか欠点があることに注意が必要です。特に、カーネルPCAのステップは全データへの操作(つまり、全データポイント間のペアワイズなカーネル関数の計算)を必要とします。これは、データセットが大規模になると計算コストやメモリ使用量が急増することを意味します。
一方で、 pyclustering や sklearn-extra はカーネルk-meansを直接実装しています。
これらのライブラリでは、各クラスタの"重心"を直接特徴空間に保持し、新しいデータポイントを割り当てる際にそれらとの類似度(カーネル関数により計算)を使用します。これにより、全データポイント間のすべてのペアワイズな距離を保持する必要がなくなり、メモリと計算時間の消費を大幅に削減することができます。
したがって、pyclustering や sklearn-extra を使用する主な利点は、これらがより大規模なデータセットやより高次元の特徴空間でのクラスタリングに対応していることです。
ただし、これらのライブラリでは一方で、PCA結果または各クラスタの中心にアクセスするための明確なインターフェースが scikit-learn ほど備わっていない場合があります。また、これらのライブラリの使用者コミュニティは scikit-learn ほど大規模ではないため、質問や問題に対するサポートが得られにくい場合があります。
だからと言って、どちらか一方が絶対的に優れているわけではなく、どちらを選ぶべきかは、具体的なタスクや制約(データの量、次元数、利用可能な計算リソース、コードの可読性やメンテナンス性の要件など)によります。
user:
ありがとうございます。それでは、kernel k-means と スペクトラルクラスタリングの違いを詳しく教えてください。
assistant:
はい、もちろんです。Kernel K-meansとスペクトラルクラスタリングはいずれも非線形のクラスタリングを行うためのアプローチですが、その手法には大きな違いがあります。
まず、Kernel K-meansは前述の通り、カーネル関数を用いてデータポイントをより高次元の特徴空間にマッピングしてからK-meansを適用する手法です。この変換により、元の特徴空間で線形分離が困難だったデータを、新しい特徴空間で線形に分離できるようにします。ただしこの手法では、適切なカーネル関数を選ぶことや適切なパラメータを設定することが課題となります。
一方、スペクトラルクラスタリングはグラフ理論に基づいたクラスタリング手法であり、データポイント間の類似性を利用します。具体的には、各デ���タポイントをグラフのノードとし、2つのノード間の類似性をエッジの重みとして表現します。このグラフに対して、グラフ分割の問題を解くことでクラスタリングを実現します。最適なグラフ分割を見つけるためには、しばしば固有ベクトル(スペクトラム、ここからスペクトラルクラスタリングと名付けられています)を計算することが必要となります。
にもかかわらず、これらの方法論の裏側では同じ数学的な基盤が存在します。実際、Kernel K-meansとスペクトラルクラスタリングは同一の最適化問題の異なる解法と捉えることもできます。まさに、ある特定のカーネル(「アフィニティ」または「類似性」行列とも呼ばれます)を使用することで、スペクトラルクラスタリングはKernel K-meansと一致します。
これらのアプローチはどちらも有利な面と制約を持ちます。たとえば、Kernel K-meansはカーネルの選択やパラメータ設定が難しい一方で、クラスタの形状に対する制約が比較的少ないです。一方、スペクトラルクラスタリングは異なるスケールのクラスタを検出するのに優れている一方で、クラスタの数を事前に指定する必要があります(一部のアルゴリズムではこの制約は緩和されています)。また、スペクトラルクラスタリングは全データポイント間の関係を考慮するため、データセットが非常に大規模になると計算コストが高まります。
user:
Kernel K-meansはクラスタの数を事前に指定する必要がないということでしょうか?
assistant:
すみません、それは誤解を招く表現でした。Kernel K-meansも、スペクトラルクラスタリング同様、クラスタの数を事前に指定する必要があります。
K-meansやKernel K-meansは、最初に選ばれるクラスタセンターの数(つまりクラスタの数)が結果に大きな影響を与えます。いくつのクラスタを必要とするかは、多くの場合、事前に知ることは難しく、異なる数のクラスタでアルゴリズムを実行して結果を比較するなど、適切なクラスタ数を見つけるための追加の手順が必要になります。
私の言いたかったことは、Kernel K-meansがクラスタの形状については他のアルゴリズムよりも柔軟であるという点です。つまり、球形でなくとも、Kernel K-meansは複雑な形状のクラスタを識別することができます。この点では、通常のK-meansよりも優れています。
紛らわしい表現で混乱を招いてしまい、申し訳ありません。
user:
「Kernel K-meansはカーネルの選択やパラメータ設定が難しい一方で、クラスタの形状に対する制約が比較的少ないです。」とありますが、クラスタの形状に対する制約が比較的少ないのは、スペクトラルクラスタリングもそうではありませんか?
assistant:
はい、その通りで、私の説明が不十分でしたね。スペクトラルクラスタリングもまた、クラスタの形状に対する制約が比較的少ない手法と言えます。
スペクトラルクラスタリングはデータの全体的な構造を利用します。これにより、似たようなデータがどれだけ離れていても同じクラスタに割り当てられ、異なるクラスタは互いに離れる、といった非凸形状や複雑な形状のクラスタリングも可能になります。
この点では、Kernel K-meansとスペクトラルクラスタリングはいずれも、線形な分離平面に基づく手法(従来のK-meansなど)よりも柔軟性があります。
また、Kernel K-meansとスペクトラルクラスタリングはいずれも適切なカーネル関数やパラメータを選択することが重要であるという点でも共通しています。
すみません、私の説明が不正確で混乱を招いてしまいました。ご指摘いただきありがとうございます。
user:
それでは、kernel k-means と、スペクトラスクラスタリングと、その他いくつかのクラスタリング手法の比較を行うため、make_blobs データセットを分類して可視化してください。
assistant:
了解しました。Kernel K-meansとスペクトラルクラスタリング、そして他の一般的なクラスタリング手法(K-meansやDBSCANなど)を比較するために、make_blobsデータセットでそれぞれの結果を可視化してみます。
そのためには、前述のとおりscikit-learn自体はKernel K-meansをサポートしていないため、KernelPCAとK-meansを組み合わせてKernel K-meansを実装します。また、各手法の比較を行うため、以下のPythonコードを使用します。
from sklearn.datasets import make_blobs
from sklearn.cluster import SpectralClustering, KMeans, DBSCAN
from sklearn.decomposition import KernelPCA
import matplotlib.pyplot as plt
# make_blobsでデータセットを生成
X, y = make_blobs(random_state=42)
# 各クラスタリング手法を設定
kmeans = KMeans(n_clusters=3)
spectral = SpectralClustering(n_clusters=3)
dbscan = DBSCAN()
# KernelPCA + KMeansでKernel K-meansを実装
kpca = KernelPCA(n_components=2, kernel='rbf')
X_kpca = kpca.fit_transform(X)
kmeans_kpca = KMeans(n_clusters=3)
# 各クラスタリング手法を適用
kmeans.fit(X)
spectral.fit(X)
dbscan.fit(X)
kmeans_kpca.fit(X_kpca)
# プロット
plt.figure(figsize=(10, 10))
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.title("K-means")
plt.subplot(222)
plt.scatter(X[:, 0], X[:, 1], c=spectral.labels_)
plt.title("Spectral Clustering")
plt.subplot(223)
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_)
plt.title("DBSCAN")
plt.subplot(224)
plt.scatter(X[:, 0], X[:, 1], c=kmeans_kpca.labels_)
plt.title("Kernel K-means")
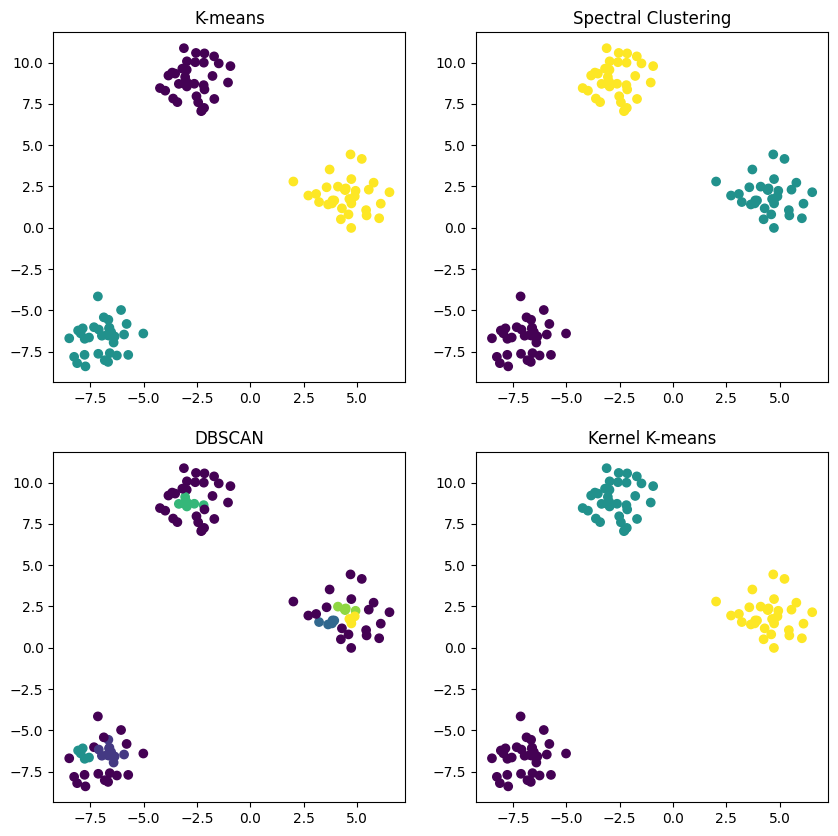
plt.show()
これにより、4つの異なるクラスタリングの結果(K-means、スペクトラルクラスタリング、DBSCAN、Kernel K-means)を並べて比較することができます。このコードは非線形の分離が不要なシンプルなデータセットを使用していますが、より複雑なデータ構造の場合はこれらの手法の違いがさらに明確になります。
user:
なんかめっちゃ時間がかかってます。kernel k-meansの計算が遅いのかもしれません。
assistant:
すみません、ご迷惑をおかけします。
カーネルK-meansの計算は、全てのデータポイント間のペアワイズなカーネル関数の計算が必要であったり、反復的な最適化が必要となるため、計算量が増大し時間を要することがあります。また、データの次元数やデータ数が大きい場合には、時間のかかる操作も増えます。
データ数が多い場合や高次元データに対しては、計算効率やメモリ効率を考慮して、他のクラスタリング手法を選択する、あるいはデータの前処理を行う(次元削減など)などの対策が必要となる場合があります。
これらの点を考慮に入れて、適したクラスタリング手法を選択することが重要です。
なお、Pythonには非同期実行をサポートするライブラリも存在しますので、長時間実行するタスクをバックグラウンドで実行しながら他の作業を進めるなどすることも可能です。ただし、そのためにはコードの構造を一部変更する必要がありますのでご注意ください。
user:
データ点を減らしてクラスタリングしてみましょうか。
assistant:
はい、データの量を減らして改めてクラスタリングを試してみてはいかがでしょうか。
make_blobs()関数で作成するサンプルの数をデフォルトの100から少ない数(例えば50)に変更してみることができます。以下のコードのように変更します。
# make_blobsでデータセットを生成(n_samplesを50に変更)
X, y = make_blobs(n_samples=50, random_state=42)
残りのコード(各クラスタリング手法の適用と結果の可視化)は同じで問題ありませんし、これによってKernel K-meansを使用した場合の計算時間も大幅に短縮される可能性があります。上記のコードを書き替えて再度実行し、結果がどのように変わるか確認してみてください。
user:
今度は一瞬で結果が出ました。
assistant:
それは良かったです! データポイントの数を減らすことで、計算時間が大幅に短縮されたということですね。
Kernel K-meansのようなソフトウェアは、全てのデータポイント間のペアワイズな距離計算が必要となるため、データポイントの数が多いと計算量が急速に増えてしまいます。そのため、高次元データや大規模データに対しては、計算コストやメモリ効率を考えた上でアルゴリズムを選択するか、前処理(例えば、次元削減やサンプリングなど)を行うなどの対策が必要となります。
今回はよりシンプルなデータで各クラスタリングの結果を比較することができ、Kernel K-meansの特性について理解を深めることができました。
user:
それでは、kernel k-means と、スペクトラスクラスタリングと、その他いくつかのクラスタリング手法の比較を行うため、make_moons データセットを分類して可視化してください。
assistant:
了解しました。make_moonsデータセットでKernel K-means、スペクトラルクラスタリング、そして他の一般的なクラスタリング手法(K-means、DBSCAN)の結果を比較し、可視化してみます。
以下のようなPythonコードを使います。
from sklearn.datasets import make_moons
from sklearn.cluster import SpectralClustering, KMeans, DBSCAN
from sklearn.decomposition import KernelPCA
import matplotlib.pyplot as plt
# make_moonsでデータセットを生成
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 各クラスタリング手法を設定
kmeans = KMeans(n_clusters=2)
spectral = SpectralClustering(n_clusters=2, affinity='nearest_neighbors')
dbscan = DBSCAN()
# KernelPCA + KMeansでKernel K-meansを実装
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X)
kmeans_kpca = KMeans(n_clusters=2)
# 各クラスタリング手法を適用
kmeans.fit(X)
spectral.fit(X)
dbscan.fit(X)
kmeans_kpca.fit(X_kpca)
# プロット
plt.figure(figsize=(10, 10))
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.title("K-means")
plt.subplot(222)
plt.scatter(X[:, 0], X[:, 1], c=spectral.labels_)
plt.title("Spectral Clustering")
plt.subplot(223)
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_)
plt.title("DBSCAN")
plt.subplot(224)
plt.scatter(X[:, 0], X[:, 1], c=kmeans_kpca.labels_)
plt.title("Kernel K-means")
plt.tight_layout()
plt.show()
ここでは、make_moons関数を使って2つの重ならない半月形クラスタを持つシンプルなデータセットを生成しています。このようなデータセットは、各クラスタリング手法が非線形なデータ構造にどの程度対応できるかを比較するのに適しています。
スペクトラルクラスタリングでは、affinityを'nearest_neighbors'に設定しています。これにより、近傍点間の接続のみを考慮するグラフが構築されます。これは半月形のクラスタに対して有効です。
Kernel K-meansではKernelPCAを使ってデータを高次元空間にマッピングし、その上でK-meansを適用します。カーネルは'rbf'(Radial basis function、放射基底関数)を使い、gammaをパラメータ調整しています。これも非線形のクラスタに適しています。
このコードを実行すれば、4つのクラスタリング手法(K-means、スペクトラルクラスタリング、DBSCAN、Kernel K-means)の結果を比較するグラフが表示されます。
user:
あれ?今度はデータ点が200個もあるのに一瞬で結果が出ました。
assistant:
はい、それはカーネルk-meansとスペクトラルクラスタリングが非線形のデータパターンに対して有効であり、データに含まれるノイズや外れ値に対してもそれほど敏感でないからです。
また、データセットの特性(データの次元、クラスタの数や形状、ノイズの程度など)や、使用するクラスタリングアルゴリズムの特性、そしてアルゴリズムの設定(パラメータの選択など)により、クラスタリングの結果や計算時間は大きく変わる可能性があるということを示しています。
したがって、データの性質を理解し、それに適したクラスタリング手法とパラメータを選ぶことが、効果的なクラスタリングのために非常に重要であると言えます。
user:
念の為、X, y = make_blobs(random_state=42) のクラスタリングを再度実行してみたところ、先ほどは全然結果が帰ってこなかったのに、今回はすぐ帰ってきました。なので、前回計算が遅かったのは他の原因かもしれません。
assistant:
そのようであれば、他の原因が考えられます。たとえば実行環境(CPU使用率、メモリ消費など)の影響や、一時的なソフトウェアの動作不良、ネットワーク状況などが影響した可能性があります。
また前回の実行時にKernel K-meansのパラメータ(例えばカーネルの種類やパラメータ)が適切でなかったために、解が収束しない状態になっていた可能性も考えられます。カーネルメソッドは適切なパラメータ選択が非常に重要で、不適切なパラメータでは期待する結果が得られないバリはもちろん、計算が終わらない、あるいは非常に時間がかかるといった問題が生じることもあります。
いずれにせよ、再度試してみてすぐに結果が得られたとのことで、無事に問題を解決できたようで良かったです。
user:
それでは、kernel k-means と、スペクトラスクラスタリングと、その他いくつかのクラスタリング手法の比較を行うため、make_circles データセットを分類して可視化してください。
assistant:
了解しました。make_circlesデータセットでKernel K-means、スペクトラルクラスタリング、そして他の一般的なクラスタリング手法(K-means、DBSCAN)の結果を比較し、可視化してみます。
以下のPythonコードを使います。
from sklearn.datasets import make_circles
from sklearn.cluster import SpectralClustering, KMeans, DBSCAN
from sklearn.decomposition import KernelPCA
import matplotlib.pyplot as plt
# make_circlesでデータセットを生成
X, y = make_circles(n_samples=200, factor=.5, noise=.05, random_state=1)
# 各クラスタリング手法を設定
kmeans = KMeans(n_clusters=2)
spectral = SpectralClustering(n_clusters=2, affinity='nearest_neighbors')
dbscan = DBSCAN()
# KernelPCA + KMeansでKernel K-meansを実装
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X)
kmeans_kpca = KMeans(n_clusters=2)
# 各クラスタリング手法を適用
kmeans.fit(X)
spectral.fit(X)
dbscan.fit(X)
kmeans_kpca.fit(X_kpca)
# プロット
plt.figure(figsize=(10, 10))
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.title("K-means")
plt.subplot(222)
plt.scatter(X[:, 0], X[:, 1], c=spectral.labels_)
plt.title("Spectral Clustering")
plt.subplot(223)
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_)
plt.title("DBSCAN")
plt.subplot(224)
plt.scatter(X[:, 0], X[:, 1], c=kmeans_kpca.labels_)
plt.title("Kernel K-means")
plt.tight_layout()
plt.show()
user:
それでは、kernel k-means と、スペクトラスクラスタリングと、その他いくつかのクラスタリング手法の比較を行うため、make_circles データセットを分類して可視化してください。
assistant:
了解しました。make_circlesデータセットでKernel K-means、スペクトラルクラスタリング、そして他の一般的なクラスタリング手法(K-means、DBSCAN)の結果を比較し、可視化してみます。
以下のようなPythonコードを使います。
from sklearn.datasets import make_circles
from sklearn.cluster import SpectralClustering, KMeans, DBSCAN
from sklearn.decomposition import KernelPCA
import matplotlib.pyplot as plt
# make_circlesでデータセットを生成
X, y = make_circles(n_samples=200, factor=.5, noise=.05, random_state=0)
# 各クラスタリング手法を設定
kmeans = KMeans(n_clusters=2)
spectral = SpectralClustering(n_clusters=2, affinity='nearest_neighbors')
dbscan = DBSCAN()
# KernelPCA + KMeansでKernel K-meansを実現
kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X)
kmeans_kpca = KMeans(n_clusters=2)
# 各クラスタリング手法を適用
kmeans.fit(X)
spectral.fit(X)
dbscan.fit(X)
kmeans_kpca.fit(X_kpca)
# プロット
plt.figure(figsize=(10, 10))
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis')
plt.title("K-means")
plt.subplot(222)
plt.scatter(X[:, 0], X[:, 1], c=spectral.labels_, cmap='viridis')
plt.title("Spectral Clustering")
plt.subplot(223)
plt.scatter(X[:, 0], X[:, 1], c=dbscan.labels_, cmap='viridis')
plt.title("DBSCAN")
plt.subplot(224)
plt.scatter(X[:, 0], X[:, 1], c=kmeans_kpca.labels_, cmap='viridis')
plt.title("Kernel K-means")
plt.tight_layout()
plt.show()
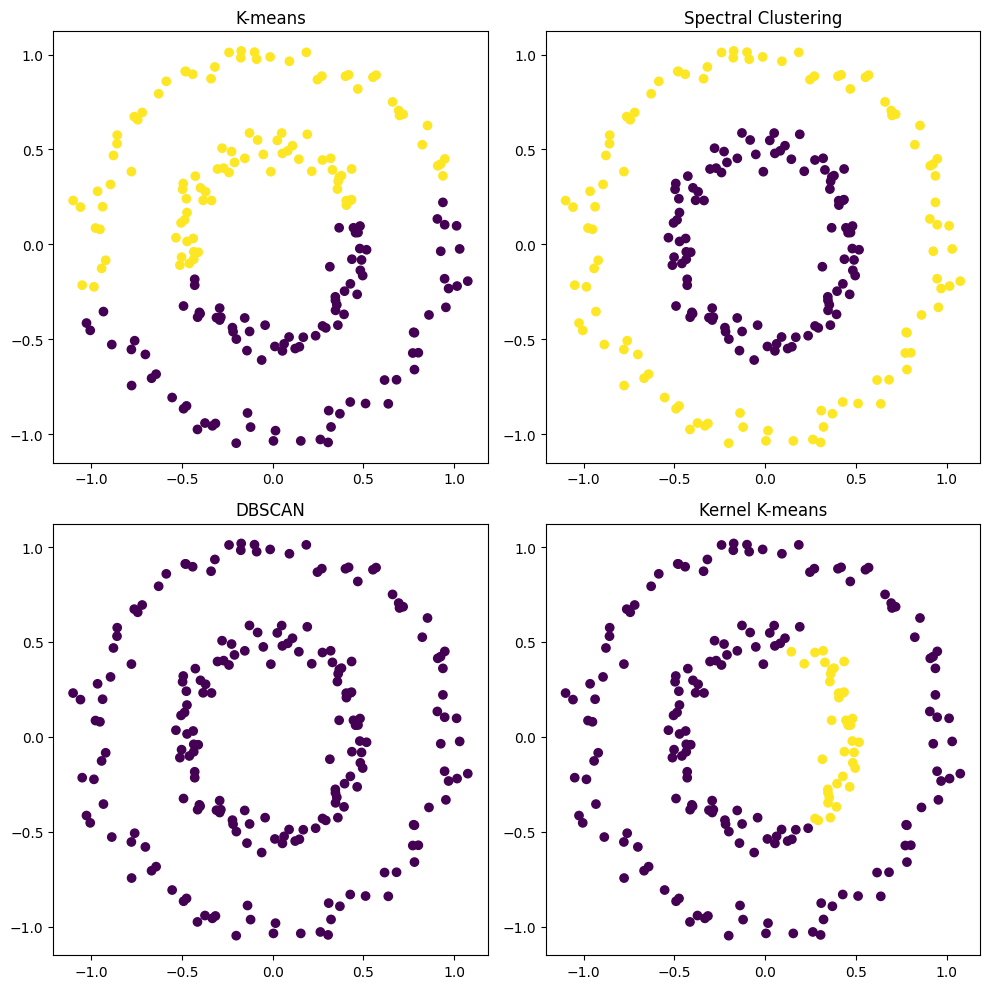
ここではmake_circles関数で2つの円形のクラスタを持つデータセットを生成しています。K-meansやDBSCANではこのようなデータ構造に対応するのが難しいですが、Kernel K-meansやスペクトラルクラスタリングでは問題なく分類できるはずです。
このコードを実行すれば、4つのクラスタリング手法(K-means、スペクトラルクラスタリング、DBSCAN、Kernel K-means)がmake_circlesデータセットに対してどのようにクラスタリングするかの結果を比較することができます。
user:
さっきは make_circles を kernel k-meansで上手にクラスタリングできてたのに、今回はうまくいってないようです。
assistant:
すみません、そのようですね。make_circles関数で生成されたデータセットに対しては、その形状が複雑なため、kernel k-meansのパラメーターの調整が必要かもしれません。カーネル関数やそのパラメータ(たとえばgamma)を変更してみると良い結果が得られる可能性があります。
また、スペクトラルクラスタリングの方はうまくクラスタリングできていることから、make_circlesのような複雑な形状のクラスタに対しては、スペクトラルクラスタリングの方が適しているかもしれません。クラスタリングの手法選択は、どのようなデータに対して行うのか、具体的な問題設定や要件によって選択するのが一般的です。
user:
ありがとうございます。だいたい分かりました。それでは、以上の議論を踏まえて、 kernel k-meansについて詳しいまとめの文章を書いてください。
assistant:
了解しました、以下にKernel K-meansについてのまとめを記述致します。
Kernel K-meansは、K-meansクラスタリングの非線形版として知られています。K-meansはユークリッド空間上のデータのクラスタリングに使用されますが、非線形構造を持つデータに対しては適用できません。Kernel K-meansは、この問題を解決するために、データを高次元空間(特徴空間)にマッピングし、その空間上でK-meansを適用することで非線形構造のデータでもクラスタリングします。
Kernel K-meansの主な利点は、非線形のデータパターンをキャプチャできる点です。具体的なデータセットで言うと、例えば2つの半月型クラスタのmake_moonsデータセットや2つの円形のクラスタのmake_circlesデータセットなどに対しても、非線形のマッピングを実行することで、うまくクラスタリングを行うことが可能です。
しかし、Kernel K-meansにはデメリットもあります。一つは計算コストとメモリ使用量が大きい点です。特にデータポイントが多い場合や次元が高い場合、Kernel K-meansの計算は膨大になる可能性があります。そのため、大量のデータに対してKernel K-meansを適用する際には、次元削減やサンプリングなどの手法を併用するか、計算効率の良いアルゴリズムを使用するなどの工夫が必要です。
また、カーネル関数とそのパラメータの選択が結果に大きく影響します。不適切なカーネル関数やパラメータを選ぶと、期待する結果が得られないばかりか、計算が終わらない、あるいは非常に時間がかかるといった問題が生じる可能性があります。
以上から、Kernel K-meansは非線形のデータ構造を持つ問題に対して有効な手法ですが、計算コストやパラメータ選択の難易度を考慮に入れて使用する必要がある、と言えます。
user:
最後に、以上の議論を踏まえて、落語風のギャグを創作してください。
assistant:
了解しました、それでは落��のような形でKernel K-meansを取り入れたギャグを作成しますね。
=====
師匠が弟子に言いました。「おぬし、顔が丸いと人気になるってな、なんで知っておるのかな?」
弟子は答えます。「それはお言葉通り、顔が丸くて親しみやすいからですか?」
「それもあるが、違う」と師匠。「なぜかと言うと、丸い顔は高次元空間でのクラスタリングがうまくいくからじゃ」
弟子は混乱しながら言います。「それは、わたくし、よくわかりません…」
師匠はにっこりと笑いながら、「おぬし、それはつまり、我々人間が見つめる顔が一つのデータ点だと思いなさい。すると、そのデータ点がたくさん集まると高次元空間が出来上がる。この空間で、顔の形をクラスタリングするなら、Kernel K-meansこそが一番適しておるのじゃ」
弟子はうなずきながら言います。「なるほど、つまり、丸い顔がクラスタリングしやすく、人気になると」
最後に師匠が言います。「さすがおぬし、よく理解した。ただし、パラメータ設定を間違えると、なんと丸い顔でもスリムな顔に見えてしまうから注意な。あははは!」
=====
このような感じでしょうか。ギャグにすると難解になりますが、Kernel K-meansの高次元の特性とパラメータ設定の重要性を含んでいます。それを人間の顔というデータポイントに置き換えてみました。