散布図
二つの特性を横軸と縦軸とし,データを打点して作る可視化手法を散布図 (Scatter Plot) といいます。
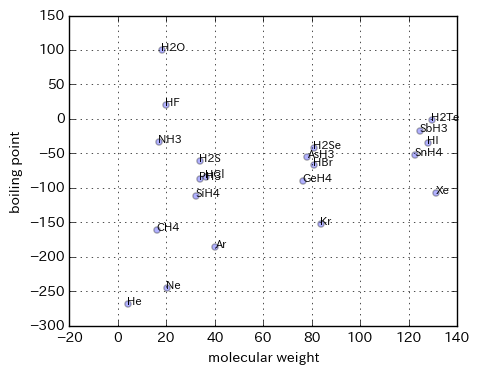
例:分子量と沸点のプロット
下記は、様々な物質の分子量(molecular weight)と沸点(boiling point)をプロットした散布図です。
線形回帰とは
回帰
説明変数 X (x1, x2, x3, ...) と目的変数 Y の関係を学習し、X から Y を予測する方法のうち、Y の取りうる値が連続値のものを「回帰」(Regression) といいます。Y の取りうる値が離散値(0か1か、ネコかイヌか、など)の場合は「分類」(Classification) といいます。
線形回帰
n 次元の散布図で各データをもっともうまく代表する (n − 1) 次元のアフィン超平面(回帰超平面)を求める手法を「線形回帰」(Linear Regression)といいます。n = 2 の場合、すなわち説明変数 X が 1変数の場合は「線形単回帰」といい、求める超平面はすなわち回帰直線になります。n > 2 の場合は「線形重回帰」といいます。
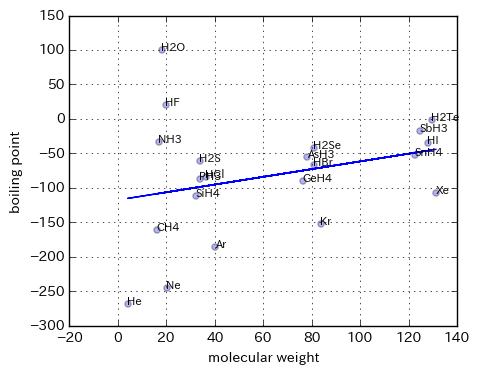
例:分子量から沸点を予測する回帰直線
線形回帰についてググると、線形回帰してよかったねという「よい例」がたくさん見つかりますので、ここではあえて「よくなかった例」として分子量から沸点を予測する回帰直線を載せておきます。この例では、誤差が大きすぎて予測にはとても使えなさそうだということが見てよくわかります。
実践
下記のデータを例に、線形回帰を行います。
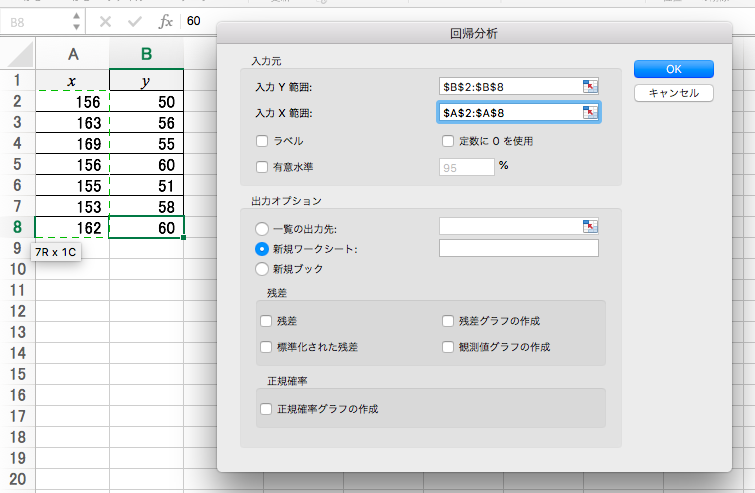
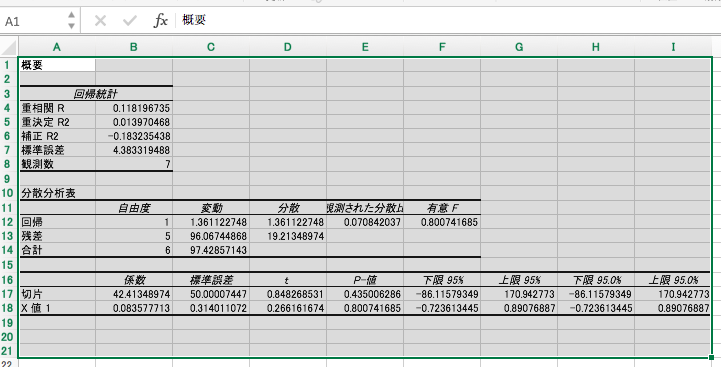
1.「データ分析」を使う方法
まず「データ」タブに「データ分析」というボタンがあるかどうか確認します。ない場合は、データ分析のアドインを追加します。(アドイン追加方法についてわからなかったらググってね!)
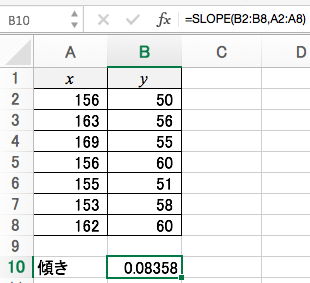
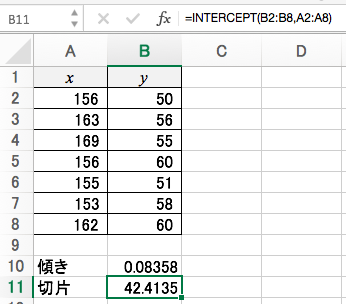
2. SLOPE関数とINTERCEPT関数を使う方法
Excelには傾きと切片を求める関数が用意されています。
アラ簡単。
3. ガチで計算する方法
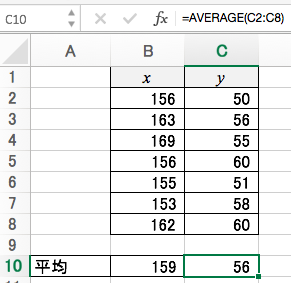
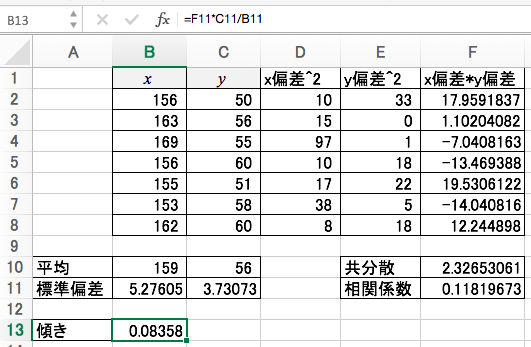
計算手法をガチで理解したい場合は以下のように計算しましょう。分からない単語があったらググってね!
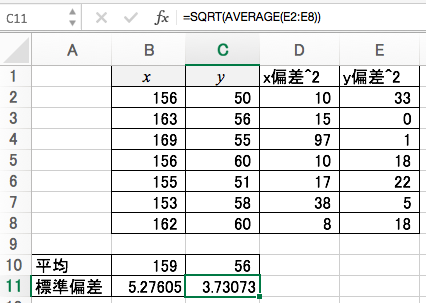
平均値
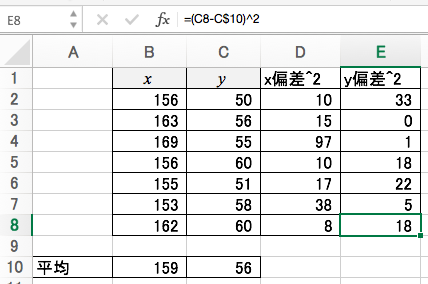
偏差の2乗
標準偏差
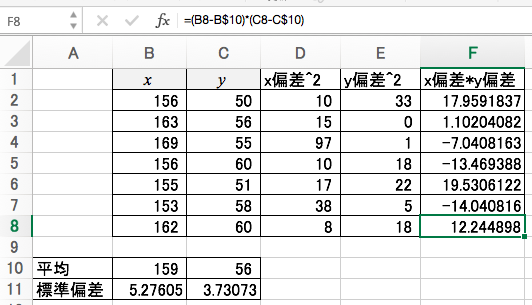
偏差積
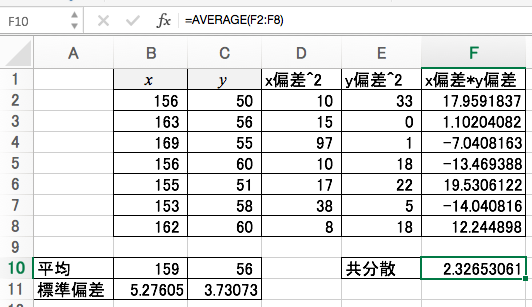
共分散
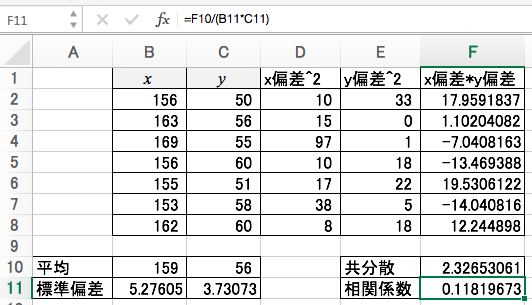
相関係数
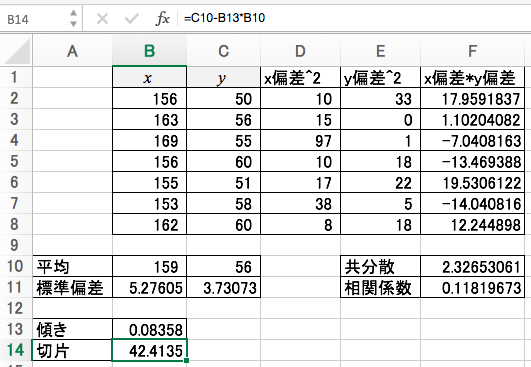
傾きと切片
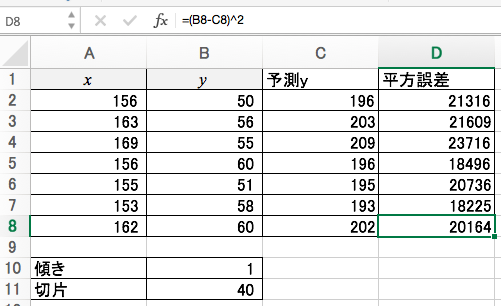
4. ソルバーを用いる方法
まず「データ」タブに「ソルバー」というボタンがあるかどうか確認します。ない場合は、ソルバーのアドインを追加します。(アドイン追加方法についてわからなかったらググってね!)
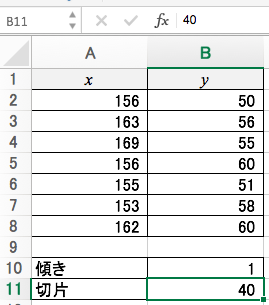
下準備
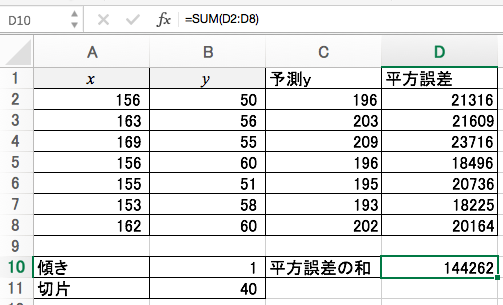
傾きと切片に、テキトーな値を入れときます。
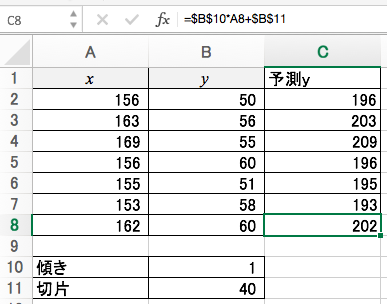
平方誤差の和を算出します。この平方誤差の和を最小にする傾きと切片をソルバーが探してくれるのです。
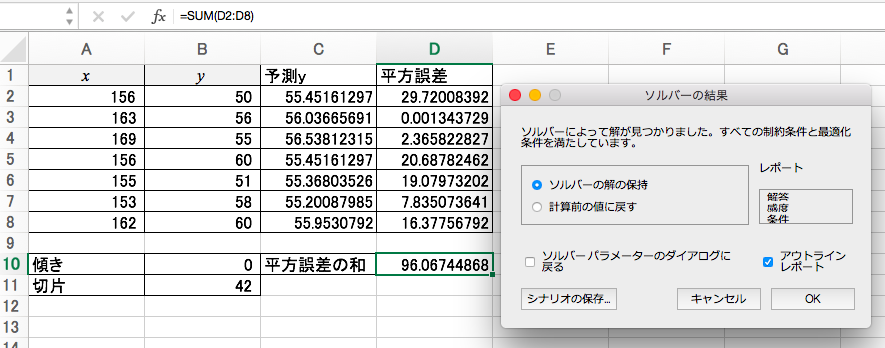
ソルバーで解決
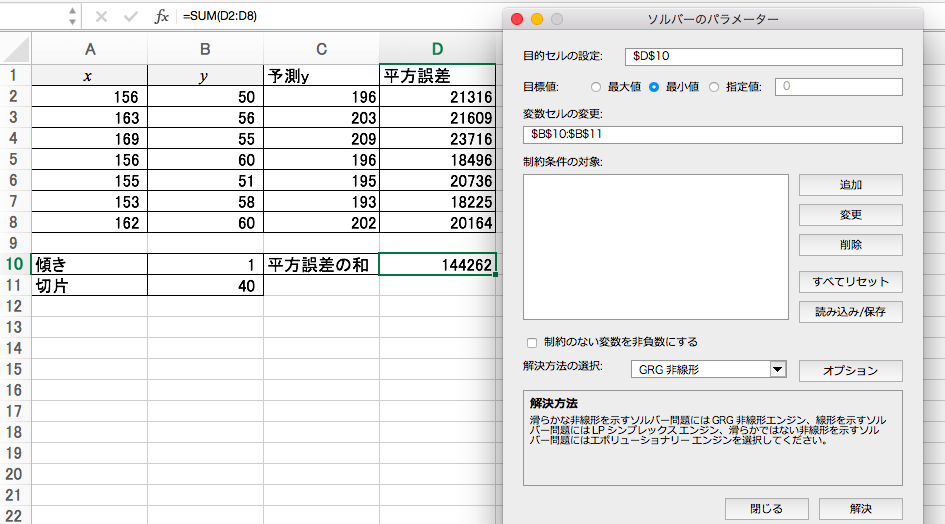
「ソルバー」ボタンを押して出てきたウインドウに、「目的セル」「変数セル」に正しく入力し、目標値を「最小値」にし、「制約のない変数を非負数にする」のチェックを外し、「解決」ボタンをクリック。
課題
今回の例では、テキトーなデータを使いました。相関係数は0.1付近ですから、驚くほど相関がありませんし、線形回帰を行う意味もありません。
そこでみなさんは、
-
相関係数が0.7以上0.9未満のデータを自作してください(データ数の目安は10個前後)。
-
自作したデータの散布図を作成してください。
-
そこに回帰直線を描き入れてください。
-
上記4つの方法で線形回帰を行ない、数字の変化を観察してください。
-
回帰直線の実データへのあてはまりの良さはどう評価すれば良いか考察してください。
-
家賃のデータ を使って、「徒歩(分)」「専有面積(㎡)」「築年数(年)」「階数(階)」の4変数から「家賃(円)」を予測する線形重回帰モデルを作成してください。
Pythonはいいぞ
Pythonを使うと、もっと簡単かつ柔軟に解けるよ。ってことで、興味のある方は引き続き 線形回帰を本当はPythonで解きたいけど表計算で解けと言われたので をご覧ください。