化学情報学にRDKitとScikit-learnで入門する

このページを見たあなたは、もう化学情報学（ケモインフォマティクス）という世界に足を踏み入れている。まずはこの世界の入り口を概観してみよう。

題材として、水溶解度を取り扱ってみます

Water solublity (logS) database http://modem.ucsd.edu/adme/databases/databases_logS.htm にある「database.dat (the SMILES file includes 1290 molecules)」 を使ってみましょう。

まず、データファイルの URL をチェックします。

http://modem.ucsd.edu/adme/data/databases/logS/data_set.dat であることが分かります。今回の目的は、このファイルの左端の列にある文字列（SMILES）から、水溶解度（logS）を予測する機械学習モデルを作成することとします。

データファイルのダウンロード

手でクリクリしてダウンロードしてもいいですが、せっかくなので urllib.request を使ってみましょう。

import urllib.request # URLで指定したファイルをダウンロードするライブラリ

url = 'http://modem.ucsd.edu/adme/data/databases/logS/data_set.dat'
urllib.request.urlretrieve(url, 'water_solubility.txt') 

('water_solubility.txt', <http.client.HTTPMessage at 0x109eb8438>)

ファイルを water_solubility.txt という名前で保存しました。

ダウンロードしたデータファイルを pandas で読み込む

読み込み方の詳細は タブ区切りデータ、コンマ区切りデータ等の読み込み をご参照ください。

import pandas as pd

df1 = pd.read_csv('water_solubility.txt', sep='\t', header=None) # データの読み込み
df1 # 読み込んだデータの確認

	0	1	2
0	O=C(C)N	60-35-5	1.58
1	NNC	60-34-4	1.34
2	O=C(C)O	64-19-7	1.22
3	N1CCCC1	123-75-1	1.15
4	O=C(N)NO	127-07-1	1.12
5	OCC(O)CO	56-81-5	1.12
6	O=C(C)N(C)C	127-19-5	1.11
7	[nH0]1cccc[nH0]1	289-80-5	1.10
8	[nH0]1ccc[nH0]c1	289-95-2	1.10
9	OCC(C(C(C(CO)O)O)O)O	50-70-4	1.09
10	O=C(CC(C)N)O	541-48-0	1.08
11	N1CCNCC1	110-85-0	1.07
12	N1CCCCC1	110-89-4	1.07
13	c1c(O)cc[nH0]c1	626-64-2	1.02
14	c1c(O)[nH0]ccc1	72762-00-6	1.02
15	O=C(O)CCCC(O)=O	110-94-1	1.00
16	C1N(C)CCOC1	109-02-4	1.00
17	O=C(N)OC	598-55-0	0.97
18	CN1C(=O)C=CC=C1	694-85-9	0.96
19	O=C(O)CCl	79-11-8	0.93
20	O=C(N)OCC	51-79-6	0.85
21	COC(=O)C1=CCCN(C)C1	63-75-2	0.81
22	c1c(O)cc(cc1)O	108-46-3	0.81
23	c1cc[nH0]cc1	110-86-1	0.76
24	N1CCNCC1C	109-07-9	0.74
25	OCC1(C(C(C(CO1)O)O)O)O	@57-48-7	0.64
26	c1c(O)c(O)ccc1	120-80-9	0.62
27	O=C(N)c1ccc[nH0]c1	98-92-0	0.61
28	C=1C(=O)NC=NC1	51953-17-4	0.59
29	O=CCC	123-38-6	0.58
...	...	...	...
1260	c1c(Cl)ccc(c1)c1ccc(cc1Cl)Cl	7012-37-5	-6.21
1261	ClC12C3C(C4C(C3Cl)O4)C(C(=C1Cl)Cl)(C2(Cl)Cl)Cl	1024-57-3	-6.29
1262	O=C(C1C(C=C(Cl)Cl)C1(C)C)OCc1cccc(c1)Oc1ccccc1	52645-53-1	-6.29
1263	Clc1c(Cl)ccc(c1c1ccccc1)Cl	55702-45-9	-6.29
1264	ClC1(C2(C3C=CC(C3C1(C(=C2Cl)Cl)Cl)Cl)Cl)Cl	76-44-8	-6.32
1265	Clc1c(c2c(Cl)cc(cc2)Cl)ccc(c1)Cl	2437-79-8	-6.51
1266	Clc1ccccc1C(c1ccc(cc1)Cl)C(Cl)(Cl)Cl	789-02-6	-6.62
1267	Cc1cccc(c1O[P+]([O-])(Oc1ccc(cc1C)O)Oc1cc(ccc1...	1330-78-5	-6.70
1268	O=C(CCCCCCCCCCCCCCC)O	57-10-3	-6.81
1269	c1c(C(C(Cl)(Cl)Cl)c2ccc(cc2)OC)ccc(c1)OC	72-43-5	-6.89
1270	O=C(c1ccccc1C(=O)OCC(CC)CCCC)OCC(CC)CCCC	117-81-7	-6.96
1271	Clc1c(c2c(Cl)ccc(c2)Cl)cc(cc1)Cl	35693-99-3	-7.00
1272	c1c(c2c(Cl)c(c(cc2)Cl)Cl)c(Cl)c(cc1)Cl	52663-62-4	-7.05
1273	c1c(c2c(Cl)c(Cl)c(c(c2)Cl)Cl)cccc1	33284-53-6	-7.16
1274	OCCCCCCCCCCCCCCCC	36653-82-4	-7.26
1275	ClC1=C(C2(C3C4CC(C=C4)C3C1(C2(Cl)Cl)Cl)Cl)Cl	309-00-2	-7.33
1276	c1c2c3c4c(cccc4c4c2cccc4)ccc3cc1	192-97-2	-7.80
1277	c1c(Cl)ccc(c1c1ccc(c(Cl)c1Cl)Cl)Cl	38380-02-8	-7.91
1278	c1c2Cc3c(c2ccc1)cc1c(cccc1)c3	243-17-4	-8.04
1279	c1c2c(ccc3c4c(ccc23)cccc4)ccc1	218-01-9	-8.06
1280	Clc1c(c2c(Cl)c(Cl)c(cc2)Cl)c(Cl)c(c(c1)Cl)Cl	52663-71-5	-8.30
1281	c1c(Cl)c(Cl)cc(c1c1ccc(c(Cl)c1Cl)Cl)Cl	35065-28-2	-8.32
1282	c1c(Cl)c(Cl)c(c(c1c1cccc(Cl)c1Cl)Cl)Cl	55215-18-4	-8.42
1283	c1c2c3c(cccc3c3c2cc2c(c3)cccc2)cc1	207-08-9	-8.49
1284	c1c2cc3c(cc4c(c3)cccc4)cc2ccc1	92-24-0	-8.60
1285	Clc1c(c2c(ccc(Cl)c2Cl)Cl)c(ccc1Cl)Cl	38411-22-2	-8.65
1286	c1c2c(ccc3c2cccc3)cc2c1ccc1ccccc12	53-70-3	-8.66
1287	c1c2c3cccc4ccc5ccc6c(c2c(cc6)cc1)c5c43	191-24-2	-9.03
1288	Clc1c(Cl)c(c2cc(c(c(Cl)c2Cl)Cl)Cl)c(c(c1Cl)Cl)Cl	40186-72-9	-10.26
1289	Clc1c(c2c(Cl)c(Cl)c(c(c2Cl)Cl)Cl)c(Cl)c(cc1Cl)Cl	52663-77-1	-10.41

1290 rows × 3 columns

このようにして、1290行3列の行列が得られました。今回の目的は、この「0列目」の文字列（SMILES）から「2列目」の数字（logS）を予測する問題を解く、ということになります。

RDKit を使ってみる

まずは化合物の絵を描いてみたい。

from rdkit import Chem

mol = Chem.MolFromSmiles("O=C(N)c1ccc[nH0]c1")

from rdkit.Chem import Draw
Draw.MolToImage(mol)

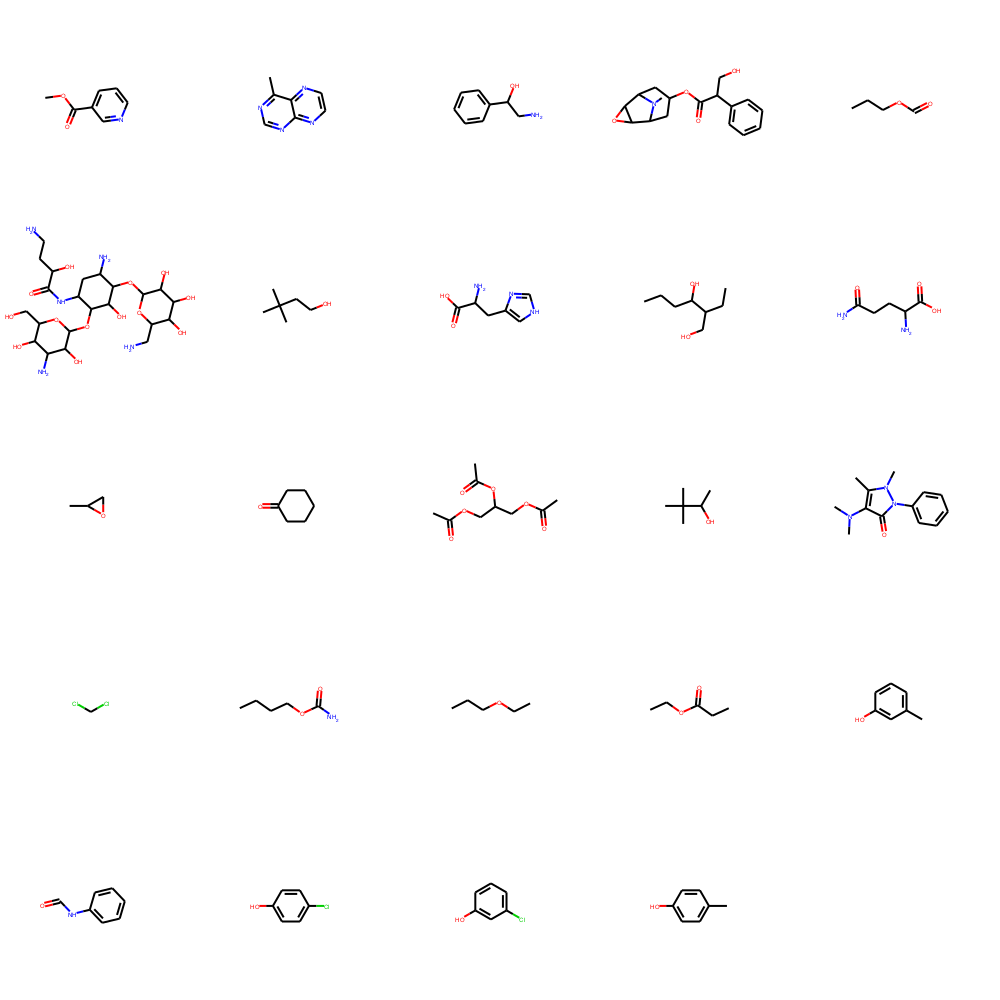
化合物の絵が描けることを確認しました。今度は、今回ダウンロードした水溶解度のデータに含まれている化合物の絵を描きましょう。ただし、全部描くのはしんどいので、先頭いくつかだけ。

mols = []
for smile in df1[0]:
    mols.append(Chem.MolFromSmiles(smile))

# 上と同じ意味。「リスト内包表記」という書き方です。
mols = [Chem.MolFromSmiles(smile) for smile in df1[0]]

Draw.MolsToGridImage(mols[100:124], molsPerRow=5, subImgSize=(200,200))

化合物フィンガープリント

化合物を数字で表現する方法のひとつとして、フィンガープリントと呼ばれるベクトルがあります。今回はその一種であるモーガンフィンガープリントを使ってみましょう。

from rdkit.Chem import AllChem
fp = AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)

fingerprint = []
for s in fp.ToBitString():
    fingerprint.append(int(s))

# 上と同じ意味
fingerprint = [int(s) for s in fp.ToBitString()]

水溶解度のデータに含まれる化合物をフィンガープリントにします。ただし、エラーが出て計算できない化合物がある場合は除外します。

import numpy as np
fingerprints = []
safe = []
for mol_idx, mol in enumerate(mols):
    try:
        fingerprint = [x for x in AllChem.GetMorganFingerprintAsBitVect(mol, 2, 2048)]
        fingerprints.append(fingerprint)
        safe.append(mol_idx)
    except:
        print("Error", mol_idx)
        continue
fingerprints = np.array(fingerprints)

Error 175

print(fingerprints.shape)
pd.DataFrame(fingerprints).head()

(1289, 2048)

	0	1	2	3	4	5	6	7	8	9	...	2038	2039	2040	2041	2042	2043	2044	2045	2046	2047
0	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0	0	0	...	0	0	0	0	0	0	0	0	0	0

5 rows × 2048 columns

フィンガープリントから水溶解度を回帰する

回帰する方法はいくつかありますが、ランダムフォレスト というものを使ってみます。

X = fingerprints
Y = df1.iloc[safe, 2]

from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor()
rf.fit(X,Y)

from sklearn.metrics import r2_score
print("R2=", r2_score(Y, rf.predict(X)))

import numpy as np
from sklearn.metrics import mean_squared_error
print("RMSE=", np.sqrt(mean_squared_error(Y, rf.predict(X))))

from sklearn.metrics import mean_absolute_error
print("MAE=", mean_absolute_error(Y, rf.predict(X)))

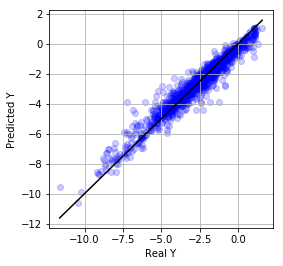
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(4,4))
plt.scatter(Y, rf.predict(X), alpha=0.2, c="blue")
plt.plot([Y.min(), Y.max()], [Y.min(), Y.max()], c="black")
plt.grid()
plt.xlabel("Real Y")
plt.ylabel("Predicted Y")
plt.show()

/Users/kot/miniconda3/envs/py3new/lib/python3.6/site-packages/sklearn/ensemble/forest.py:248: FutureWarning: The default value of n_estimators will change from 10 in version 0.20 to 100 in 0.22.
  "10 in version 0.20 to 100 in 0.22.", FutureWarning)


R2= 0.9381194414671183
RMSE= 0.5054545837347694
MAE= 0.34466386277058253

うん、あまり混みいったことしてない割には、いい感じ。では、サポートベクトル回帰ってやつも使ってみましょうか。

from sklearn.svm import SVR
svr = SVR()
svr.fit(X,Y)

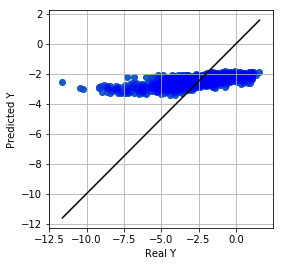
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(4,4))
plt.scatter(Y, svr.predict(X), alpha=0.2, c="blue")
plt.plot([Y.min(), Y.max()], [Y.min(), Y.max()], c="black")
plt.grid()
plt.xlabel("Real Y")
plt.ylabel("Predicted Y")
plt.show()

/Users/kot/miniconda3/envs/py3new/lib/python3.6/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
  "avoid this warning.", FutureWarning)

ありゃ。だめだこりゃ。サポートベクトルマシンは、パラメーター調整をグリグリ頑張って初めて真価を発揮する手法なので、デフォルトパラメータを使うと良くないことが多いのです。

さあ、次にやることは？

• 化合物の表現方法として、フィンガープリント以外にもさまざまな「化学構造記述子」があります。フィンガープリントにも、いろんなフィンガープリントがあります。

• 機械学習手法として、ランダムフォレスト やサポートベクトルマシン以外にも色々な手法があります。

• パラメータ調節方法として、グリッドサーチやベイズ最適化などの方法があります。

• 機械学習で注意すべき点として「過学習」という現象があり、それを防ぐための方法論として「交差検定」などがあります。

まだまだ学ぶべきことは多いけれども、ここまで読んだあなたは今、こう言える。

ケモインフォの「世界」に入門したッ！

ゴゴゴゴゴゴ...