ChatGPTとPythonで学ぶ主成分分析 #Python

皆さんこんにちは。今日も引き続きChatGPT先生をお迎えして、「ChatGPTとPythonで学ぶ主成分分析」というテーマで雑談したいと思います。それではChatGPT先生、よろしくお願いします。

assistant:

こんにちは！今日は主成分分析についてお話しする予定です。主成分分析は、多変量データの次元を削減するための手法で、機械学習やデータ分析で頻繁に使用されます。Pythonのライブラリであるscikit-learnを用いて具体的にどのように主成分分析を行うか解説していきたいと思います。

さて、まずは主成分分析（PCA：Principal Component Analysis）について説明します。PCAはデータの特徴を捉えるために、次元が高いデータをより低い次元で表現するための手法です。特に、データの分散が最大となる方向を見つけ出し、その方向を新しい軸としてデータを表現し直します。この時、最も分散が大きい軸を第一主成分、次に分散が大きい軸を第二主成分と言います。

PythonでPCAを行うには、scikit-learnのPCAクラスを使用します。使用する際の一般的な手順は以下の通りです。

PCAクラスのインスタンスを生成
データセットに対してfitメソッドを呼び出し、データを学習
transformメソッドを呼び出し、データを変換

具体的なコードは次のようになります。

from sklearn.decomposition import PCA

# データを用意
X = ...  

# PCAクラスのインスタンスを生成
pca = PCA(n_components=2)  # ここでは2次元に削減

# データに対してfit
pca.fit(X)

# データをtransform
X_pca = pca.transform(X)

こうすると、PCAクラスは学習データセットから主成分を見つけ、それを基にデータセットを変換します。PCAを用いることで高次元データを低次元にすることができ、可視化や機械学習モデルの学習時間の短縮に利用することができます。

user:

主成分分析について学ぶために、ペンギンデータセットを使って主成分分析を行い、累積寄与率を可視化し、主成分プロットを可視化し、ローディングプロットも可視化してください。

assistant:

了解しました。先ずは必要なライブラリをインポートし、データを読み込みましょう。

import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import numpy as np

# ペンギンデータを読み込みます
penguins = sns.load_dataset('penguins')

# 数値データのみ抽出
penguins_num = penguins.select_dtypes(include=np.number).dropna()

# データを標準化します。PCAは変数のスケールに影響を受けるため、標準化が推奨されます。
scaler = StandardScaler()
penguins_standard = scaler.fit_transform(penguins_num)

次にPCAを実行し累積寄与率を計算し、可視化しましょう。

# PCAを実行
pca = PCA()
penguins_pca = pca.fit_transform(penguins_standard)

# 寄与率の累積を計算しプロット
cum_explained_var_ratio = np.cumsum(pca.explained_variance_ratio_)
plt.plot(range(1, len(cum_explained_var_ratio)+1), cum_explained_var_ratio, marker='o')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.show()

実装後、x軸に主成分の数、y軸に累積寄与率を表示したグラフが表示されます。

次に主成分プロットを作成しましょう。

# DataFrameに変換し、プロット
penguins_pca_df = pd.DataFrame(penguins_pca, columns=[f'PC{i+1}' for i in range(penguins_pca.shape[1])])
sns.scatterplot(data=penguins_pca_df, x='PC1', y='PC2')
plt.show()

各点がペンギンの個体を表し、それらがPC1とPC2という新しい座標軸でプロットされます。

最後に、ローディングプロットを作成しましょう。

# DataFrameに変換
loadings = pd.DataFrame(pca.components_.T, columns=[f'PC{i+1}' for i in range(penguins_pca.shape[1])], index=penguins_num.columns)

# プロット
sns.scatterplot(data=loadings, x='PC1', y='PC2')
for i in range(loadings.shape[0]):
    plt.text(loadings.iloc[i, 0], loadings.iloc[i, 1], loadings.index[i])
plt.show()

ローディングプロットでは、各元の変数がPC1とPC2のどの程度影響を与えているかが可視化されています。

user:

主成分プロットはデータラベルで色分けしてください。

assistant:

ペンギンデータセットには"species"という列が含まれていて、種別による色分けをすることができます。

まず対応するラベルデータの準備が必要です。ここではpenguinsの'species'列を参照しましょう。欠損値の除去も行います。

# ラベルデータの準備
species = penguins['species'].dropna()

次にプロットを作成します。

# 主成分プロットの作成（色分け付き）
plt.figure(figsize=(10,7))
sns.scatterplot(data=penguins_pca_df, x='PC1', y='PC2', hue=species, palette='viridis')
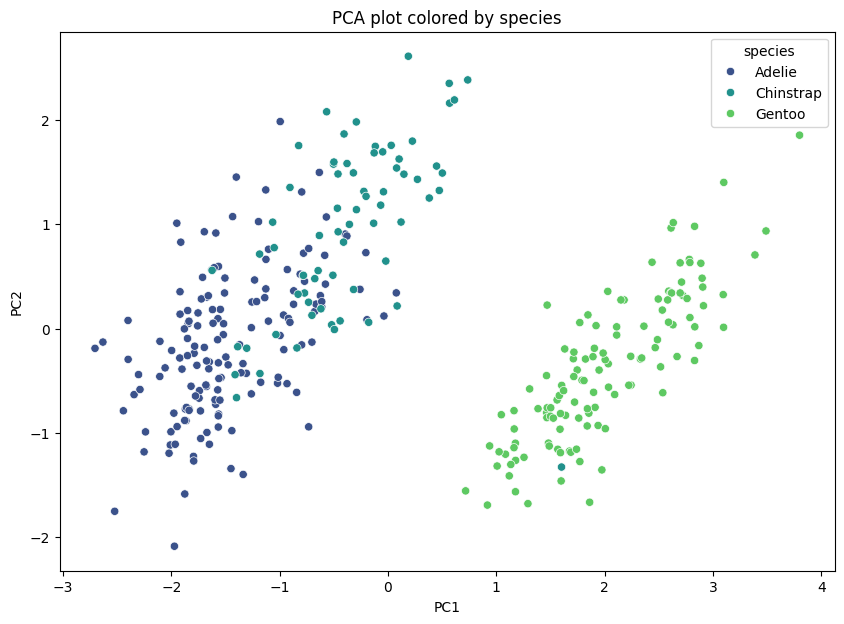
plt.title('PCA plot colored by species')
plt.show()

各点が1つのペンギンを表し、それぞれの種別によって色が分けられています。これにより、さまざまな種別のペンギンがPC1とPC2でどのように分布しているかを視覚的に理解することができます。

user:

データラベルごとに、各変数がどんな分布になっているか可視化してください。

assistant:

了解しました。データラベルごとに各変数がどのような分布になっているかを可視化するには、Seabornのpairplot()関数が便利です。次のようにコードを実行します。

# ペアプロットの作成
sns.pairplot(penguins.dropna(), hue='species')
plt.show()

これにより、"species"（種別）によって色分けされた各変数のペアに対する散布図とヒストグラムを一度に確認することができます。各ペンギンの種別が、それぞれの特徴量（"bill_length_mm"や"bill_depth_mm"、"flipper_length_mm"、"body_mass_g"）にどのように影響を与えているかを視覚的に確認することができます。

user:

主成分分析について学ぶために、カリフォルニアデータセットを使って主成分分析を行い、累積寄与率を可視化し、主成分プロットを可視化し、ローディングプロットも可視化してください。データ点は住宅価格に応じて色付けしてください。

assistant:

まず必要なライブラリをインポートし、データを読み込みます。

from sklearn.datasets import fetch_california_housing

# California Housingデータの読み込み
data_bunch = fetch_california_housing(as_frame=True)
data = data_bunch.frame

# 使用するカラム（ターゲットは除く）
columns = data.columns[:-1]

# データを標準化します。PCAは変数のスケールに影響を受けるため、標準化が推奨されます。
scaler = StandardScaler()
data_standard = scaler.fit_transform(data[columns])

次にPCAを実行し累積寄与率を計算し、可視化しましょう。

# PCAを実行
pca = PCA()
data_pca = pca.fit_transform(data_standard)

# 寄与率の累積を計算しプロット
cum_explained_var_ratio = np.cumsum(pca.explained_variance_ratio_)
plt.plot(range(1, len(cum_explained_var_ratio)+1), cum_explained_var_ratio, marker='o')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.title('PCA cumulative explained variance ratio')
plt.show()

次に主成分プロットを作成しましょう。データ点は住宅価格に応じて色付けします。

# DataFrameに変換し、プロット
data_pca_df = pd.DataFrame(data_pca, columns=[f'PC{i+1}' for i in range(data_pca.shape[1])])
data_pca_df['MedianHouseValue'] = data['MedHouseVal']
plt.figure(figsize=(10,7))
sns.scatterplot(data=data_pca_df, x='PC1', y='PC2', hue='MedianHouseValue', palette="viridis")
plt.title('PCA plot colored by median house value')
plt.show()

最後にローディングプロットを作成しましょう。

# DataFrameに変換
loadings = pd.DataFrame(pca.components_.T, columns=[f'PC{i+1}' for i in range(data_pca.shape[1])], index=columns)

# プロット
sns.scatterplot(data=loadings, x='PC1', y='PC2')
for i in range(loadings.shape[0]):
    plt.text(loadings.iloc[i, 0], loadings.iloc[i, 1], loadings.index[i])
plt.title('PCA Loading plot')
plt.show()

こうしてローディングプロットが作成されます。ローディングプロットでは各元の変数が主成分にどの程度影響を与えているかが可視化されます。

user:

あれ？住宅価格は連続値だと思ってましたが離散値でしたか。

assistant:

申し訳ありません、説明が不足していました。カリフォルニアデータセットにある住宅価格（MedHouseVal）は連続値のデータです。

上述の散布図では、住宅価格（MedHouseVal）を色にマッピングしていますが、これは住宅価格の値に基づいて色相が変化する、つまり連続的なカラーマップを使用しています。つまり、散布図上の点の色が異なるほど、住宅価格の違いが大きいことを示しています。

加えて、Scatter plotの色分けについて更に詳しく説明しますと、seabornのscatterplot関数はhueパラメータに連続値を与えると自動的に連続的なカラーマップを使用します。そのため、住宅価格（MedHouseVal）のような連続値を色にマッピングする場合には個別の色のカテゴリーではなく連続的なカラーマップが使用されるということです。

user:

先ほどの散布図では離散値のように描画されていますが、連続値のような描画に変えてください。

assistant:

申し訳ありません、ご要望の内容に対する理解が足りませんでした。連続値のような描画に変更するため、scatter関数を使用してプロットを再度作成します。

# DataFrameに変換し、プロット
data_pca_df = pd.DataFrame(data_pca, columns=[f'PC{i+1}' for i in range(data_pca.shape[1])])
data_pca_df['MedianHouseValue'] = data['MedHouseVal']

# 連続値を色に変換するためのカラーマップを作成
cmap = plt.get_cmap("viridis")
norm = plt.Normalize(data['MedHouseVal'].min(), data['MedHouseVal'].max())

fig, ax = plt.subplots(figsize=(10,7))
sc = ax.scatter(data=data_pca_df, x='PC1', y='PC2', c=data_pca_df['MedianHouseValue'], cmap=cmap, norm=norm)
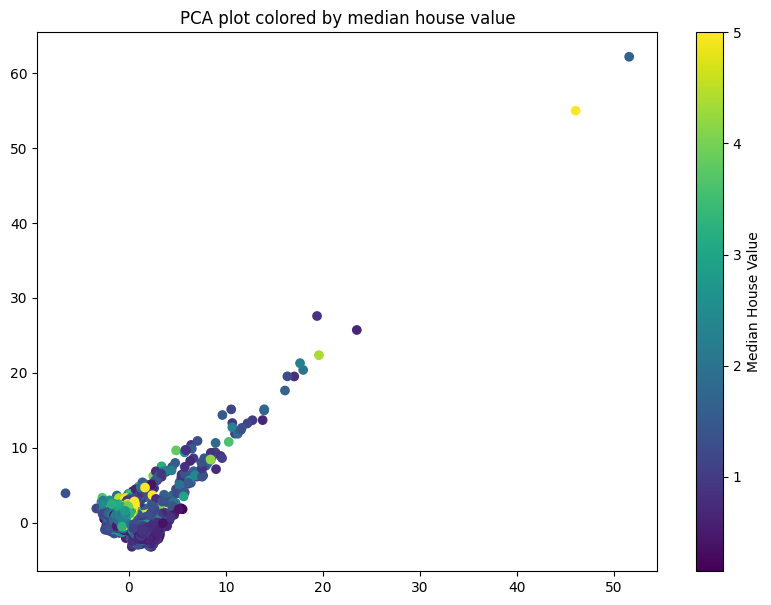
plt.title('PCA plot colored by median house value')
fig.colorbar(sc, ax=ax, label='Median House Value')
plt.show()

このようにすると、住宅価格が連続値としてカラーマッピングされ、散布図が色彩豊かになり、価格の変化がもっと細かく表現されます。カラーバーも追加して、色が具体的にどの住宅価格を指しているかを示しています。

user:

主成分プロットについて、どのように解釈すればよいか詳しく教えてください。

assistant:

はい、もちろんです。主成分プロット（あるいはPCAプロット）は、多次元データを2次元または3次元に削減して描画するもので、それらのプロットはデータの全体的な分布やグループ間の相関関係を捉えるのに役立ちます。それでは、主成分プロットをどのように解釈するかについて説明します。

分布: プロット上の点々は個々のデータポイントを表現しており、それらの分布を見ることでデータ全体の構造を理解することができます。すなわち、データポイントが密集している領域はデータが頻出する領域を示し、逆にデータポイントが少ない領域はデータが稀な領域を示します。
主成分の寄与: 主成分分析では、元の特徴空間にある大きな分散の方向が第一主成分として捕捉されます。第一主成分軸（PC1）に沿ったデータの広がりは、データの分散が最大であることを示します。同様に、第二主成分（PC2）は第一主成分と直交し、残りの最大分散を捕捉します。これらの軸により、可能な限り多くの情報を捉える新しい座標軸が生成されます。
グループ間の違い: 色分けや形状によるマーキングをプロット内で使うことで（あるいは3次元プロットや複数の主成分を使うことで）、データポイント間の関係性または異なるクラスタやグループの間での関係性を視覚的に探求することが可能になります。グループ間に明確な分界がある場合、それらのグループは互いに異なる傾向を持つと解釈できます。
矢印（ローディング）: 主成分プロットのバージョンによっては、各主成分の負荷（つまり、元の特徴が第一主成分や第二主成分にどの程度寄与しているかを示す因子）を矢印で表現することがあります（これをローディングプロットと呼びます）。矢印の方向と長さは、その特徴が主成分にどの程度影響を及ぼすかを示します。

したがって、主成分プロットは、より高次元のデータを低次元で視覚化するための出力であり、それによりデータ全体の洞察を得ることが可能になります。ただし、元の特徴空間から一部の情報が失われることに注意する必要があります。入力特徴が無数にある場合や、ノイズ特徴がある場合には特に有用です。

user:

累積寄与率について詳しく教えてください。

assistant:

主成分分析（PCA）では、元の変数の情報を可能な限り維持しつつ、次元を削減することが目指されます。これは、元のデータセットの分散が最大となる方向（=新しい特徴量、つまり主成分）を見つけ出すことで達成されます。

PCAが生成する各主成分は、元のデータの全体分散に対してどれだけの情報（分散）を説明できるかという「寄与率」を持ちます。第一主成分は最も分散を説明できる情報を持つことになり、第二主成分はそれに次ぐ分散を説明できる情報を持ちます。なお、これらの主成分はそれぞれが直交するように作られるため、他の主成分と情報が重複することはなく、同時に全体分散の一部を個別に説明します。

この各主成分の寄与率を累積（足し合わせ）したものが「累積寄与率」となります。例えば、第三主成分までの累積寄与率が80％である場合、それは元のデータの分散の80％が最初の3つの主成分だけで説明できることを意味します。つまり、元の多次元データセットの情報の大部分が3つの主成分だけで一応の精度で再現できるということです。

累積寄与率をプロットして閾値（例えば90％や95％など）を設けることで、その次元数で元のデータのどれだけの情報を保持できるかを見積もることができます。これを見ることにより、何個の主成分を用いれば特定の情報量をカバーできるのかを把握したり、元のデータセットの分散がどの程度の次元に集約されているのかを理解することができます。

user:

主成分分析についてより深く理解するために、主成分分析をスクラッチで実装し、ペンギンデータセットに対して累積寄与率を可視化し、主成分プロットを可視化し、ローディングプロットを可視化してください。

assistant:

もちろんです、PCAの基本原理を理解するために、スクラッチでPCAを実装してみましょう。

PCAの基本的な手順は以下の通りです：

データの標準化: PCAは変数のスケールに影響を受けるので、事前にデータの標準化を行います。
共分散行列の計算: 標準化されたデータから共分散行列を計算します。
固有値と固有ベクトルの計算: 共分散行列の固有値と固有ベクトルを計算します。これらは、PCAの主成分と寄与率を決定します。
主成分の選択: トップN固有値に対応する固有ベクトルを選択します。これが主成分となります。
新しいデータセットの作成: 選択した主成分を使って、元のデータを新しい低次元空間に変換（射影）します。

以下にPythonでPCAをスクラッチで実装したコードを示します。

import numpy as np
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

# データの読み込みと準備
dataset = sns.load_dataset('penguins').dropna()
X = dataset.iloc[:, 2:6]  # 使用する特徴量

# データの標準化
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# 共分散行列の計算
cov_matrix = np.cov(X_std.T)

# 固有値と固有ベクトルの計算
eigen_vals, eigen_vecs = np.linalg.eig(cov_matrix)

# 固有値の大きい順に固有ベクトルを並び替える（これが主成分）
order = np.argsort(eigen_vals)[::-1]
eigen_vals = eigen_vals[order]
eigen_vecs = eigen_vecs[:, order]

# 累積寄与率の計算
cum_explained_var_ratio = np.cumsum(eigen_vals) / np.sum(eigen_vals)

# 累積寄与率のプロット
plt.plot(range(1, len(cum_explained_var_ratio)+1), cum_explained_var_ratio, marker='o')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.title('PCA cumulative explained variance ratio')
plt.show()

# 最初の2つの主成分でデータを変換
X_pca = X_std.dot(eigen_vecs[:, :2])

# 主成分プロット
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1])
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('PCA plot')
plt.show()

# ローディングプロット
loadings = pd.DataFrame(eigen_vecs[:, :2], columns=['PC1', 'PC2'], index=X.columns)
sns.scatterplot(data=loadings, x='PC1', y='PC2')
for i in range(loadings.shape[0]):
    plt.text(loadings.iloc[i, 0], loadings.iloc[i, 1], loadings.index[i])
plt.title('PCA Loading plot')
plt.show()

こうして構築したPCAモデルを使用して、ペンギンデータセットを低次元（2次元）に変換します。各データポイント（ペンギン）はプロット上で一意の点として表現され、ローディングプロットは元の変数（ビルの長さ、ビルの深さなど）がそれぞれの主成分にどの程度寄与しているかを示します。累積寄与率のプロットは、2つの主成分が元のデータのどれだけの情報量（分散量）を保持しているかを示します。

user:

できました。ですが主成分の正負が逆転してますね。

assistant:

PCAの結果は、固有ベクトルの向き（正または負）に依存しません。つまり、主成分の正負が逆転しても、その結果の解釈に影響を与えることはありません。主成分（固有ベクトル）は、データの分散が最大となる方向を表しています。この方向は、矢印の向きによって決まります。2つの向き（正または負）が可能であるため、主成分の正負が逆転しても（つまり、矢印の向きが反対になっても）、それは同じ方向を指し示していると解釈できます。

したがって、主成分の正負が逆転するという現象は、PCAの結果を解釈する上で問題になることはありません。実際のところ、PCAの実装やデータのランダムな性質により、主成分の正負はどちらになるかが変わることがあります。主な点は、主成分が捉えているデータの分散の方向性であり、それが正または負のどちらであるかは重要ではないということです。

user:

主成分分析の計算手順はよく分かりました。主成分分析における共分散行列や、固有値と固有ベクトルの果たす役割について詳しく教えてください。

assistant:

主成分分析（PCA）では、変数間の共分散を活用して、データの分散が最大となる新たな軸（主成分）を見つけ出します。

共分散行列: 共分散行列は、データセット内の各変数間の共分散を表します。ここでの共分散は、二つの変数がそれぞれの平均からどれだけ同時に離れるかを表しています。つまり、一つの変数が増加するときに他の変数が増加する傾向にあるか、あるいは減少する傾向にあるかを示します。
固有値と固有ベクトル: 共分散行列の固有値と固有ベクトルは、初めてPCAで使われます。これらは、次の意味を持ちます：
- 固有ベクトル（主成分）: 共分散行列の固有ベクトルは、主成分を表します。つまり、データの分散が最大となる方向を示す新たな特徴軸です。各主成分は互いに直交します（非相関）。固有ベクトルは全ての長さが1になるように正規化され、それぞれが主成分の方向を定義します。
- 固有値: 共分散行列の固有値は、それぞれの主成分（固有ベクトル）がデータの分散をどの程度説明しているかを示します。言い換えれば、それぞれの固有ベクトルによって捉えられる情報量を表します。固有値が大きければ大きいほど、その主成分が持つ情報量も多いと言えます。

したがって、PCAでは、共分散行列を計算し、その共分散行列の固有値と固有ベクトルを求めることで、データの主要なパターンを捉えた新しい特性を見つけ出すことができます。これらは元のデータの分散の大部分を保持しているため、データの次元を削減するのに利用することができます。

user:

なるほど、ありがとうございます。線形の次元削減法は他にもあると思いますが、それらと主成分分析との違いを詳しく教えてください。

assistant:

はい、線形の次元削減手法は主成分分析（PCA）以外にもいくつか存在します。その中で特によく使用されるものに、線形判別分析（Linear Discriminant Analysis、LDA）と独立成分分析（Independent Component Analysis、ICA）があります。各手法の大まかな違いは以下の通りです：

線形判別分析（LDA）: LDAはPCAと非常に似ていますが、主な違いは、LDAが教師あり学習アルゴリズムである点です。つまり、対象のデータがラベル付けされている場合に使用できます。LDAは、異なるクラスを最もよく分離できる特徴空間を見つけようとします。具体的には、クラス間の分散を最大化し、クラス内の分散を最小化します。
独立成分分析（ICA）: ICAもまた、次元削減手法の一つですが、PCAとは違い、ICAはデータの統計的な独立性を引き出そうとします。ICAは特に、混合した信号を個々の独立した成分に分離する際によく使用されます（この例としては、カクテルパーティー問題が有名です）。PCAがデータの分散を最大化しようとするのに対し、ICAはデータの統計的な独立性を最大化します。

これらの手法のどれを使用するかは、分析の目的や持っているデータに依存します。PCAはデータの分散が最大となる方向を見つけ出しますし、LDAはクラスを最もよく分離できる方向を見つけ出します。一方、ICAは信号を最も独立した成分に分離しようとします。したがって、具体的な問題設定や目標に応じて、適切な次元削減手法を選択します。

user:

特異値分解と主成分分析は類似点ありませんでしたか？

assistant:

はい、特異値分解（SVD）と主成分分析（PCA）は密接な関係にあります。

特異値分解（SVD）は、任意のm×n行列を特異ベクトルと特異値から構成される3つの行列の積に分解する手法です。具体的には、m×n行列Xは以下のように分解できます：

X = UΣV^T

ここで、UとVは直交行列（U^T U = V^T V = I）、Σは対角行列（主対角成分が特異値）です。

一方主成分分析（PCA）では、共分散行列に固有値分解を適用することで、データの分散を最大にする新しい特徴を見つけ出します。

以下が、PCAとSVDの関連性です：

奇異値分解は、任意の実数行列に適用できますが、主成分分析は主に共分散行列に適用されます。
PCAによって生成された主成分は、実はデータ行列の特異ベクトルです。
PCAにおける各主成分の寄与度は、それに対応する特異値の二乗に比例します。

つまり、PCAとSVDは密接に関連しており、SVDはPCAを適用するための強力なツールとも言えます。データ行列を標準化し（各特徴量から平均を引き、分散で割ります）、その結果得られた行列にSVDを適用すると、その左特異ベクトルがPCAの主成分に一致します。また、それぞれの主成分の寄与度は、対応する特異値の平方に比例します。

したがって、PCAとSVDはいずれも高次元データをより低次元の構造に圧縮するための強力なツールであり、ともにデータの最も重要な特徴を抽出するのに使われます。その具体的な適用方法や解釈は、データや問題設定によって異なります。

user:

ありがとうございました。以上の議論を踏まえて、主成分分析について詳しくまとめてください。

assistant:

主成分分析（PCA）は、主に高次元データをより低い次元空間に変換するための統計的な手法です。データの各特徴量間の共分散を考慮して新しい特徴軸（主成分）を導出し、データの分散が最大となる方向を特定します。

PCAの手順は以下の通り：

データの標準化：各特徴量のスケールを統一します。
共分散行列の計算：各特徴量間の共分散を計算します。
固有値と固有ベクトルの計算：共分散行列の固有ベクトルが新たな特徴軸（主成分）を、固有値はその主成分の持つ情報量を表します。
主成分の選択と射影：元のデータを新しい軸に射影し、次元を削減します。

PCAはデータの可視化、ノイズの除去、特徴抽出、データの圧縮など、多くの用途に利用されます。また、PCAの出力は特異値分解（SVD）と密接な関係にあり、実際にSVDはPCAを行うためのツールとしてよく利用されます。

しかし、PCAの結果はデータと主成分の間の線形関係を仮定しているため、非線形構造を持つデータに対しては他の次元削減手法（カーネルPCA、t-SNE、UMAPなど）が必要となります。また、PCAは教師なし手法なので、ターゲット変数との関係は考慮されません。この点を考慮に入れる場合は、教師ありの次元削減手法（線形判別分析LDAなど）を使用します。

user:

最後に、これまでの議論を踏まえた面白ギャグを創作してください。

assistant:

データサイエンティストがバーで友人に会った時の会話。

データサイエンティスト: 「最近、主成分分析のプロジェクトに取り組んでいてね、データを整理するのが大変だよ。」

友人: 「それなら、頼むことがあるんだけど、私のクローゼットを主成分分析してくれないか？私の服が多すぎて何を着ていいかわからないんだ。」

データサイエンティスト: 「それなら、最初に服のカテゴリー別に共分散行列を作った方が良いかもしれないね。そうすれば、どの服が一緒に着ることで最適化できるかが分かるだろう。でも、それは主成分分析じゃなくて、プリンシパル・クローゼット・分析だね！」

ChatGPTとPythonで学ぶ 主成分分析

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

user:

assistant:

ChatGPTとPythonで学ぶ主成分分析