機械学習の理解-はじめの一歩

はじめに

機械学習ってずいぶん前から騒がれて、色んな記事とか本とか出てて、もうどれから読んだら良いの！？って状態の方に本当に単純な話からしていこうと思う。

参考文献
今回の話は「ニューラルネットワーク自作入門」という本の内容を抜粋して書いております。足りない部分があったりするかと思いますが、興味がありましたら、読んでみればよいかと思います。

この本の出版社であるマイナビ出版社様から記事への投稿を制限付きで許諾していただきました。誠にありがとうございます。下記URLです。

Tariq Rashid “Make Your Own Neural Network” (新納浩幸監訳『ニューラルネットワーク自作入門』マイナビ出版)
https://book.mynavi.jp/ec/products/detail/id=65933
https://www.amazon.co.jp/gp/product/4839962251/

また、本の著者である Tariq Rashid氏 からも許可していただきました。
下記、Tariq氏のブログとgithubのURLです。
http://makeyourownneuralnetwork.blogspot.com/
https://github.com/makeyourownneuralnetwork

前提としての理解

最低限以下のことぐらいは理解していないと何言ってるか分からないかもしれません。
できるだけ簡単に書くつもりです。

• コンピュータは単純な計算をしてるだけってことを理解している。
• 人間はある画像を見て「これは猫の顔だ」とかすぐに理解できる。
• コンピュータは画像を見て「これは猫の顔だ」とすぐには理解できない。
• 中学レベルの数学が理解できている。

人間とコンピュータの違い

人間は脳を使って以下のように質問に答える。

コンピュータは考えてはいない。単に計算機である。

例えば、「4×3」の入力に対して、以下のように計算して、結果を出力する。

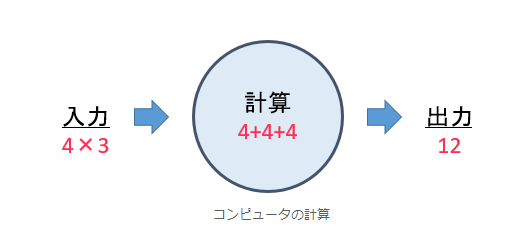
コンピュータによる予測

はここで、キロメートルをマイルに変換するコンピュータを作成するとする。

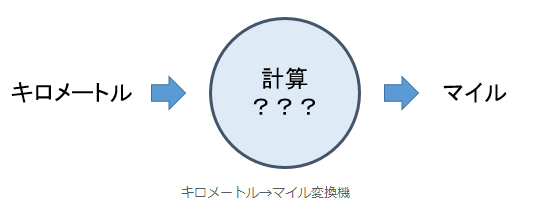
この時、私たちは「キロメートルの数が2倍になれば、マイルの数も2倍になる」ということを知っています。直感でわかりますよね。
これを数学的式で表すと下記の通りになります。

$$マイル=キロメートル*α(&alphaは定数)$$

また、私たちには下記のデータが与えられているとします。

データ	km	マイル
1	0	0
2	100	62.137

人間であれば、この時点で「逆算して定数αの値計算できるじゃん」と答えを出すことができるが、ここでは機械が少しずつ学習していく様子を見ていきましょう！

コンピュータが定数αを求めるまで

コンピュータはまだ定数αを知るすべはない。そこでとりあえずランダムに定数αを決定する。（ここでは0.5とする）

定数α＝0.5とした場合、「100kmは50マイルである。」となる。
しかしデータの例②をみると100km=62.137マイルである。

コンピュータはデータ例②と比較して、誤差を計算します。
$$62.137-50=12.137$$

誤差を計算した結果、12.137分だけ不足していることがわかります。
それでは、この誤差を小さくするためには定数αをどうすればよいでしょうか。

答えは単純です。定数αの値を増やせばいいのです。
$$定数α=0.6$$にしてみましょう。

すると100×0.6＝60
「100キロメートルは60マイルである。」とコンピュータは計算しました。
先ほどよりは誤差が小さくなりましたが、まだ__62.137-60＝2.137__の誤差があります。
コンピュータは「まだ定数αの値を増やさないと」と予測するわけです。

それでは定数αを0.7としてみましょう。同じ計算をすると
「100キロメートルは70マイルである。」となり、-7.863の誤差があります。

ようやくここで、コンピュータは「定数αの値を減らさないと」と予測できます。そして、「定数αは0.6より大きく、0.7より小さい数字である。」ことがわかります。

あとは繰り返し

先ほどの例で定数αを0.6から0.7に増やしたが、増やしすぎである事が分かった。__次は微調整していこう。__と予測するわけです。

定数αを今度は0.61にして次は0.62、0.63…というふうに増やしていきます。
そして、誤差がマイナスになれば、また繰り返し。
0.621、0.622…

そうして、正しいマイルになるまで繰り返してようやく
定数αは0.62137であると結果を出します。

せっかくだからプログラム(c++)で予測機を作成

# include <stdio.h>
# include <stdlib.h>
# include <iostream>
# include <iomanip>

using namespace std;

int main(void)
{
  double data[2][2] = {{0, 0}, {100, 62.137}};             // kmとマイルのデータ（正解データ）
  double alpha=0, prediction=0, diff=1, adjustment=0.1;    // 定数alpha、予測したマイルの値、正解データとの差、調整値
  bool small_flag = false, large_flag = false;             // フラグ（正解データより下回ったか、上回ったか）

  srand(time(NULL));    // 乱数の初期化
  alpha = rand() % 10;
  alpha = alpha / 10;   // alphaをランダムで選択(0.1~0.9)

  cout << "alpha | prediction | diff" << endl;

  /* 予測機  */
  while(diff != 0){
    prediction = data[1][0] * alpha; // 100km * alpha
    diff = data[1][1] - prediction;  // 予測したマイルが正解データ(62.137)とどれだけズレているか

    cout << alpha << " | "<< prediction << " | " << diff << endl; //ただのターミナル表示

    // 差がマイナスなら調整値分引く、プラスなら足す
    if(diff < 0){
      alpha = alpha - adjustment;
      small_flag = true;
    }else{
      alpha = alpha + adjustment;
      large_flag = true;
    }

    // フラグが両方trueなら、調整値を10分の1にする。
    if(small_flag == true && large_flag == true){
      adjustment = adjustment * 0.1;
      small_flag = false;
      large_flag = false;
      cout << "" << endl;
      cout << "alpha | prediction | diff" << endl;
    }
  }

  // 結果表示
  cout << "" << endl;
  cout << "alpha is " << alpha << endl;

  return 0;
}

出力結果は以下のようになった。

./a.out
alpha | prediction | diff
0.7 | 70 | -7.863
0.6 | 60 | 2.137

alpha | prediction | diff
0.7 | 70 | -7.863
0.69 | 69 | -6.863
0.68 | 68 | -5.863
0.67 | 67 | -4.863
0.66 | 66 | -3.863
0.65 | 65 | -2.863
0.64 | 64 | -1.863
0.63 | 63 | -0.863
0.62 | 62 | 0.137

alpha | prediction | diff
0.63 | 63 | -0.863
0.629 | 62.9 | -0.763
0.628 | 62.8 | -0.663
0.627 | 62.7 | -0.563
0.626 | 62.6 | -0.463
0.625 | 62.5 | -0.363
0.624 | 62.4 | -0.263
0.623 | 62.3 | -0.163
0.622 | 62.2 | -0.063
0.621 | 62.1 | 0.037

alpha | prediction | diff
0.622 | 62.2 | -0.063
0.6219 | 62.19 | -0.053
0.6218 | 62.18 | -0.043
0.6217 | 62.17 | -0.033
0.6216 | 62.16 | -0.023
0.6215 | 62.15 | -0.013
0.6214 | 62.14 | -0.003
0.6213 | 62.13 | 0.007

alpha | prediction | diff
0.6214 | 62.14 | -0.003
0.62139 | 62.139 | -0.002
0.62138 | 62.138 | -0.001
0.62137 | 62.137 | -7.10543e-15
0.62136 | 62.136 | 0.001

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.621369 | 62.1369 | 0.0001

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 1e-05

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 1e-06

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 1e-07

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 9.99999e-09

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 9.99989e-10

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 9.99876e-11

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 9.99734e-12

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 9.87654e-13

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 9.23706e-14

alpha | prediction | diff
0.62137 | 62.137 | -7.10543e-15
0.62137 | 62.137 | 0

alpha | prediction | diff

alpha is 0.62137

なんかdouble型だから、めっちゃ細かいとこまで計算される…。有効桁数の制限儲ければ、もう少し綺麗に解答出せると思いますが、めんどくさいし、解答出てるから良しとします。

終わりに

いかがだったでしょうか。
今回の話はとても簡単な話ですが、機械がどのように予測をしていくかがわかりやすかったのではないでしょうか。
ここで理解していほしいのはコンピュータが予測するとはどういうフローで行われているのかということ。決して、人間のように逆算をするわけではないということです。

私事

人生何とでもなれ-新卒4ヶ月で退職、再就職までの道
私事ではございますが、こちらに書いた記事は詳しく、自身のブログにまとめております。
また、機械学習について、分類に関しても記事をまとめております。
よければ、アクセスしてみください。