機械学習に必要な高校数学やり直しアドベントカレンダー Advent Calendar 2016の3日目の記事です。
2日目の記事を書いて下さったseri_kさんが紹介されたチャート式の参考書、懐かしいですね。「大学への数学」と並んで、高校の頃使っていた教材です。
で、そんな高校数学の参考書に出てくるもので、機械学習の分野でも頻出するのが $e$ という記号。シグモイド関数やソフトマックス関数などで使われますし、誤差関数でよく出てくる交差エントロピー誤差にも自然対数という形で出てきます。この $e$、高校数学で習うものですが、今回の高校数学やり直しアドベントカレンダーを機に復習してみます。
eの定義を見てみると...
教科書や参考書を見ると出てくる$e$の定義は以下の通りです。
$$e = \lim_{t \to 0}(1+t)^{\frac{1}{t}}$$
値としては $e=2.71828182845904・・・・・・・・・$ となるわけですが、いまいちピンときません。
そこで、ちょっと別の考え方で $e$ を見てみます。
指数関数
その前に、まず指数関数を復習します。$f(x)=2^x$をグラフに書くと、以下のようになります。
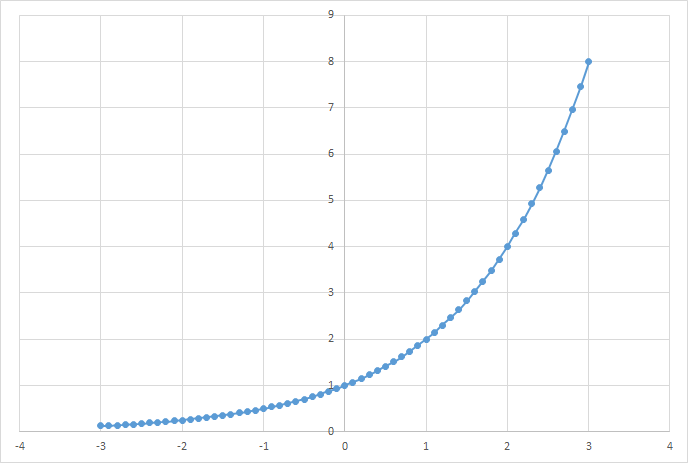
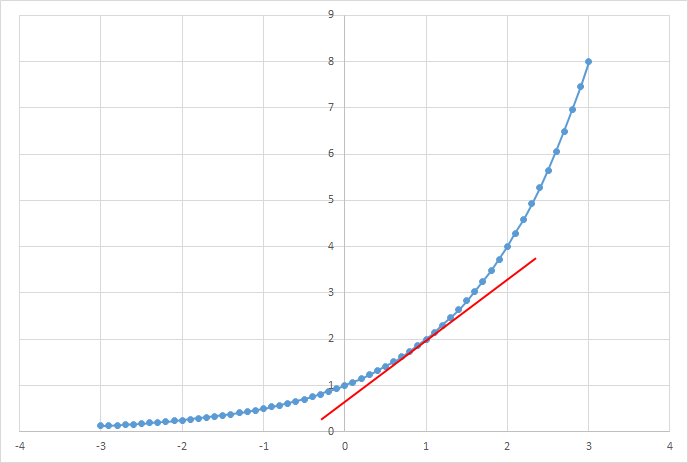
この関数における任意の $x$ の位置における傾きを求めてみます。例えば $x=1$ におけるこのグラフの傾き、つまり以下のグラフの赤線で示した接線の傾きですが、数値微分の考え方を用いて近似値を求めてみます。
$x=1$から±0.01の範囲の値と、その$f(x)$の値を見てみると、
$x=0.99$のとき、$f(x)=2^{0.99}=1.986185...$
$x=1.01$のとき、$f(x)=2^{1.01}=2.013911...$
です。ここから、接線の傾きの近似値は$$\frac{2.013911 - 1.986185}{1.01-0.99} = 1.386305$$となります。
ここで、$x=1$のときの$f(x)$の値を求めると、
$$f(1)=2^1=2$$ですね。なので、接線の傾きとの差は、$$2-1.386305=0.613695$$です。
では、$f(x)=3^x$の時の$x=1$における接線の傾きはどうでしょうか?
先ほどと同様に、±0.01の範囲での近似値を求めてみると、
$x=0.99$のとき、$f(x)=3^{0.99}=2.967222...$
$x=1.01$のとき、$f(x)=3^{1.01}=3.033140...$
ですので、接線の傾きの近似値は$$\frac{3.033140 - 2.967222 }{1.01-0.99} = 3.295903$$となります。
ここで、$x=1$のときの$f(x)$の値を求めると、$$f(1)=3^1=3$$ですね。なので、接線の傾きとの差は、$$3-3.295903=-0.295903$$です。
同様に$f(x)=2.5^x$の接線の傾きの近似値は、$2.290759$。$f(1)$との差は、$0.209241$です。
$f(x)=2^x$のとき、$x=1$の接線の近似値は1.386305。$f(1)$の値と接線の近似値の差は0.613695。
$f(x)=2.5^x$のとき、$x=1$の接線の近似値は2.290759。$f(1)$の値と接線の近似値の差は0.209241。
$f(x)=3^x$のとき、$x=1$の接線の近似値は3.295903。$f(1)$の値と接線の近似値の差は-0.295903。
上記3つの指数関数の値と、その点における接線の傾きとの差は、それほど大きくありません。
この調子で探っていくと、$f(1)$の値と接線の傾きの差が0、つまり$$f(1)="x=1のときの接線の傾きの値"$$となる$f(x)$が見つかるのではないでしょうか?
これこそが、$e=2.71828182845904・・・・・・・・・$なのです。
上記と同様の計算を、この$e$の数値でやってみましょう。ちょっと桁数が多いので、$e=2.71828$で計算してみます。
$f(x)=2.71828^x$のとき、
$x=0.99$のとき、$f(x)=2.71828^{0.99}=2.691233...$
$x=1.01$のとき、$f(x)=2.71828^{1.01}=2.745599...$
ですので、接線の傾きの近似値は$$\frac{2.745599 - 2.691233}{1.01-0.99} = 2.718323476$$となります。$f(1)=2.718128$に非常に近い値が算出されています。eの数値の小数以下の桁数を増やして精度を上げれば、より近い値になります。
つまり、先ほど書いた$f(1)="x=1の時の接線の傾きの値"$となるわけですが、この関係は$x=1$のときだけに成り立つものではありません。$f(x)=e^x$では、$x$がどんな値の時にでもこの関係式は成り立ちます。上記の計算を、$x$の値を2や3など色々変えて試して見てください。どの値にしても、$f(x)$の値が接線の傾きの値と同じになると思います。
ここで思い出して欲しいのが微分です。微分は、グラフ上では関数の接線の傾きを表します。その接線の傾きが、$f(x)=e^x$のときには、$f(x)$の値と同じになるのです。
ですので、$f(x)=e^x$のときには、その微分は$f'(x)=e^x$になります。
この$e=2.71828182845904・・・・・・・・・$ですが、他にもいろいろ面白い性質を持つ不思議な数のようです。そのため、このような本まで出版されています。ご興味があれば是非。
・不思議な数eの物語
・対数eの不思議―無理数eの発見からプログラミングまで
機械学習に必要な高校数学やり直しアドベントカレンダー Advent Calendar 2016の4日目は、kazutarosuさんです。