Accord.NETによる機械学習 - パーセプトロンの実装

機械学習の１分野であるパーセプトロンの勉強をするときに参考にしたのが、以下のページです。
http://d.hatena.ne.jp/echizen_tm/20110606/1307378609

RGB形式で入力した色が暖色系なのか寒色系なのかを返すプログラムを例題として扱っています。実際にコード書いて、パーセプトロンの基礎を紹介しています。誤差関数（＝損失関数）として確率的勾配降下法についても説明＆具体的なプログラムを紹介してるページです。とても参考になりました。

で、これと同じプログラムを、.NET Framework用の機械学習ライブラリであるAccord.NETを使って書いてみました。

作ったプログラム

今回作ったプログラムはこんな感じのものです。

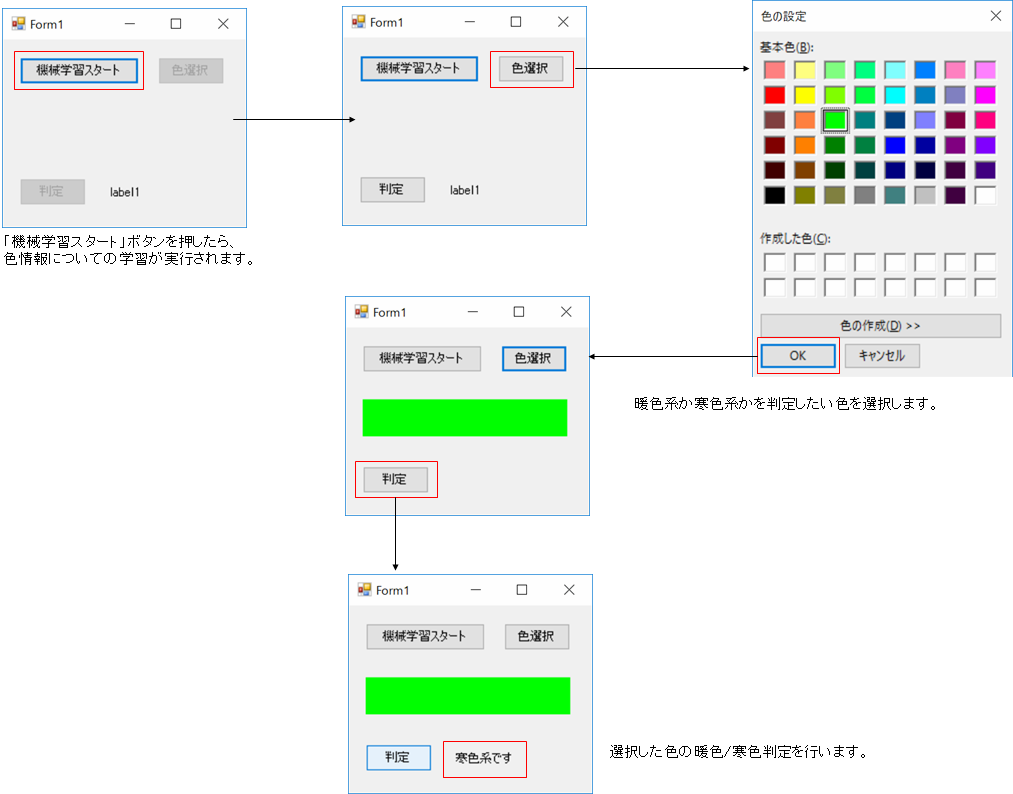
パーセプトロンによる判定

実装の前に、パーセプトロンについて学んでおくと、より理解が深まります。こちらのページの解説がとても分かりやすいです。
http://hokuts.com/2015/11/24/ml1_func/
http://hokuts.com/2015/11/25/ml2_perceptron/

上記のページでは、パラメータが２つの例で紹介しているので２次元の座標でパーセプトロンを説明しています。データを2分割する直線の傾きを得るために大量のデータを読み込ませ、すこしずつ直線の傾きを修正していきます。この「傾きの修正」が機械学習に当たります。

今回扱う題材も同様です。指定した色を暖色系/寒色系に分ける平面の傾きを求めます。上記のページと違うのは、色情報はRとGとBの３つのパラメータが出てくるので、3次元座標で考えなくてはならない点です。ですが基本は同じです。

具体的にはこんな感じですね。

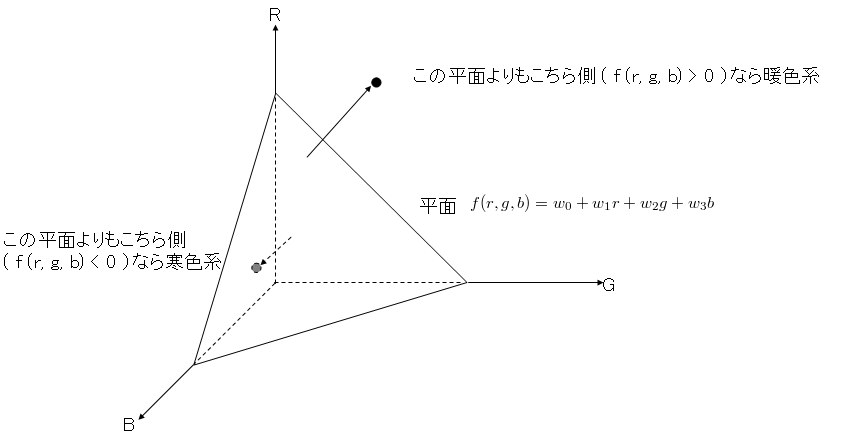図1 - 今回のプログラムを図示したもの

この平面の数式をパーセプトロンで表すと、次のようになります。

図2 - 平面の数式を図示したもの

パーセプトロンをより正確に示した図が以下になります。

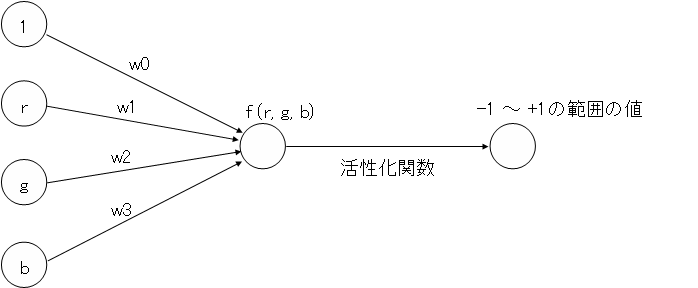
図3 - パーセプトロン

算出されたf(r,g,b)の値を、-1～+1の範囲に収める特殊な関数（これがここで言う活性化関数）を通し、0より小さければ寒色系、0以上なら暖色系と判別します。
（※ 活性化関数は-1～+1に収める以外にも、色々なものがあります。今回は-1を寒色系、+1を暖色系とするので、-1～+1に収める活性化関数を用います）

この平面を決める係数であるw0～w3を、機械学習により求めていきます。

Accord.NETによる実装

以下、今回作ったプログラムになります。Windowsフォームのデザイナ部分は省略しています。

Form1.cs

using Accord.Neuro;
using Accord.Neuro.ActivationFunctions;
using Accord.Neuro.Networks;
using AForge.Neuro.Learning;
using System;
using System.Drawing;
using System.Windows.Forms;

namespace AccordPerceptronTest
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        #region 学習データ
        #region 色データ
        private double[][] inputs = {
            new double[] {214,182,65,1},
            new double[] {173,140,56,1},
            new double[] {64,0,178,1},

            ～～ 中略 ～～

            new double[] {184,242,140,1},
            new double[] {145,174,105,1},
        };
        #endregion
        #region 教師データ
        // 暖色系 : { 1 } , 寒色系 : { -1 }
        private double[][] outputs = {
            new double[] { 1 },
            new double[] { 1 },
            new double[] { -1 },

            ～～ 中略 ～～

            new double[] { -1 },
            new double[] { -1 },
        };
        #endregion
        #endregion

        DeepBeliefNetwork network = null;
        double[] selectedColor = new double[4];

        /// <summary>
        /// 機械学習
        /// </summary>
        private void Training()
        {
            // ネットワークの生成
            network = new DeepBeliefNetwork(
                new GaussianFunction(),          // 活性化関数の指定
                inputsCount: 4,                  // 入力層の次元
                hiddenNeurons: new int[] { 1 }); // 出力層の次元

            // ネットワークの重みをガウス分布で初期化する
            new GaussianWeights(network).Randomize();
            network.UpdateVisibleWeights();

            // DBNの学習アルゴリズムの生成  
            var teacher = new PerceptronLearning(network);

            // 学習実行。同じデータを1000回学習させる。
            for (int i = 0; i < 1000; i++)
               teacher.RunEpoch(inputs, outputs);

            // 重みの更新
            network.UpdateVisibleWeights();
        }

        /// <summary>
        /// 機械学習開始
        /// </summary>
        /// <param name="sender"></param>
        /// <param name="e"></param>
        private void button1_Click(object sender, EventArgs e)
        {
            Training();

            MessageBox.Show("完了しました");

            button2.Enabled = true;
            button3.Enabled = true;
        }

        /// <summary>
        /// 色選択
        /// </summary>
        /// <param name="sender"></param>
        /// <param name="e"></param>
        private void button2_Click(object sender, EventArgs e)
        {
            colorDialog1.ShowDialog(this);
            Color tempColor = colorDialog1.Color;

            panel1.BackColor = tempColor;

            selectedColor[0] = Convert.ToDouble(tempColor.R);
            selectedColor[1] = Convert.ToDouble(tempColor.G);
            selectedColor[2] = Convert.ToDouble(tempColor.B);
            selectedColor[3] = 1;

            label1.Text = string.Empty;
        }

        /// <summary>
        /// 判定
        /// </summary>
        /// <param name="sender"></param>
        /// <param name="e"></param>
        private void button3_Click(object sender, EventArgs e)
        {
            double[] output = network.Compute(selectedColor);

            //  一番確率の高いクラスのインデックスを得る
            string result = output[0] >= 0 ? "暖色系です" : "寒色系です";

            label1.Text = result;
        }
    }
}

ここで注目すべき点は２つ。色データと教師データ、および機械学習を行うTraining()メソッドです。

色データと教師データ

色データは {r, g, b, <バイアス項>}という配列になっています。Accord.NETでは学習データをdouble型の2次元配列で受け付けるので、ここでもdouble型2次元配列で定義しています。

そして重要になってくるのが教師データです。ここに、定義した色データが暖色系か寒色系かを指定します。このデータの並びが重要です。色データの並び順と教師データの並び順は同じでなくてはなりません。例えば、色データの中の0番めの要素である{214,182,65,1}の教師データは、教師データ2次元配列の0番めの要素である{ 1 }になります。

この学習データと教師データの並び順の関係は、Accord.NET使い方なので、覚えておいてください。

学習データ

#region 学習データ
#region 色データ
private double[][] inputs = {
    new double[] {214,182,65,1},　// 色データ(a)。これに対応する教師データは、教師データ(1)になる。
    new double[] {173,140,56,1},　// 色データ(b)。これに対応する教師データは、教師データ(2)になる。
    new double[] {64,0,178,1},    // 色データ(c)。これに対応する教師データは、教師データ(3)になる。

    ～～ 中略 ～～

    new double[] {184,242,140,1}, // 色データ(d)。これに対応する教師データは、教師データ(4)になる。
    new double[] {145,174,105,1}, // 色データ(e)。これに対応する教師データは、教師データ(5)になる。
};
#endregion
#region 教師データ
// 暖色系 : { 1 } , 寒色系 : { -1 }
private double[][] outputs = {
    new double[] { 1 },　　　　　// 教師データ(1)
    new double[] { 1 },         // 教師データ(2)
    new double[] { -1 },        // 教師データ(3)

    ～～ 中略 ～～

    new double[] { -1 },        // 教師データ(4)
    new double[] { -1 },        // 教師データ(5)
};
#endregion
#endregion

機械学習部分

そして、上記で用意した学習データで機械学習させ、平面の式のw0～w3を求めていくプログラムが以下の部分になります。

機械学習

/// <summary>
/// 機械学習
/// </summary>
private void Training()
{
    // ネットワークの生成
    network = new DeepBeliefNetwork(
        new GaussianFunction(),          // 活性化関数の指定
        inputsCount: 4,                  // 入力層の次元
        hiddenNeurons: new int[] { 1 }); // 出力層の次元

    // ネットワークの重みをガウス分布で初期化する
    new GaussianWeights(network).Randomize();
    network.UpdateVisibleWeights();

    // DBNの学習アルゴリズムの生成（誤差関数を決める部分）
    var teacher = new PerceptronLearning(network);

    // 学習実行。同じデータを1000回学習させる。
    for (int i = 0; i < 1000; i++)
       teacher.RunEpoch(inputs, outputs);

    // 重みの更新
    network.UpdateVisibleWeights();
}

このプログラム中の「network = new DeepBeliefNetwork(<活性化関数>, <入力層次元>, <出力層次元>)」で、図3に示したパーセプトロンが作られます。
今回、r, g, b, およびバイアス項の4つの入力値が入力層に入るので、入力層の次元は4、出力層は1つなので、出力層の次元には1を指定します。

そして活性化関数の指定です。Accord.NETでは、-1～+1の範囲に計算結果を収める関数「GaussianFunction()」と、0～+1の範囲に計算結果を収める「BernoulliFunction()」が用意されています。

今回は-1を寒色系、+1を暖色系として扱うために、GaussianFunction()を指定しています。

パーセプトロンのネットワーク（機械学習的な用語でいうとニューラルネットワーク）を作成したら、平面の数式中の係数w0～w3（これらを重みと言います）を初期化します。ここではガウス分布で初期化しました。

そして学習アルゴリズムの生成です。これは誤差関数（損失関数とも言います）の設定です（つまり、重みw0～w3の値を修正する関数です）。先ほど紹介したこちらのページで説明されている勾配降下法などはその１種です。ここではPerceptronLearning()を選びました。

以上でネットワーク、活性化関数、誤差関数の指定が完了です。これで学習データを読み込ませ、機械学習をさせられるようになりました。この機械学習をさせるメソッドが、「RunEpoch(<学習データ>, <教師データ>)」です。今回は、同一の色データ/教師データを1000回繰り返し学習させています。

以上で機械学習は終了です。

実際の暖色/寒色判定は、学習させたnetworkインスタンスのCompute()メソッドに色データをdouble型配列で渡してください、その結果が0より大きいか小さいかで判断できます。

閑話休題 : Accord.NETで用意されている活性化関数

Accord.NETでは、以下の2種類の活性化関数が用意されています。
　・BernoulliFunction()
　・GaussianFunction()
それぞれのソースコード中の活性化関数のロジックは以下のようになっています。

BernoulliFunction.cs

/// <summary>
/// Calculates function value.
/// </summary>
///
/// <param name="x">Function input value.</param>
/// 
/// <returns>Function output value, <i>f(x)</i>.</returns>
///
/// <remarks>The method calculates function value at point <paramref name="x"/>.</remarks>
///
public double Function(double x)
{
    return (1 / (1 + Math.Exp(-alpha * x)));
}

この数式を見てみると、BernoulliFunction()に実装されている活性化関数はシグモイド関数のようですね。

GaussianFunction.cs

/// <summary>
/// Calculates function value.
/// </summary>
///
/// <param name="x">Function input value.</param>
/// 
/// <returns>Function output value, <i>f(x)</i>.</returns>
///
/// <remarks>The method calculates function value at point <paramref name="x"/>.</remarks>
///
public double Function(double x)
{
    double y = alpha * x;

    if (y > range.Max)
        return range.Max;
    else if (y < range.Min)
        return range.Min;
    return y;
}

GaussianFunction()に実装されている数式は、指定した最大値/最小値でクリッピングしているだけのようです。デフォルトの最大値/最小値はそれぞれ、+1/-1となっています。