はじめに
この記事は、物工/計数 Advent Calendar 2021 22日目の記事です。
初めましての方は初めまして。計数工学科B4のまさよしです。B4なので当然卒論に追われているため、typoとかは許してください(理論パートもめっちゃ端折りました)。
テーマは最近流行りの?多様体上の最適化です。直交行列からなる多様体上の最適化により、混合された画像から元の画像を復元することを目標にします。
問題設定
画像が3枚あるとしましょう(もちろん3枚じゃなくても構いません)。$\mathrm{img}$を画像を格納した配列として、$\mathrm{img}[i]$ $(i=0, 1, 2)$ が各画像を表すとします。突然ですがその画像たちがなぜかある直交行列$A$によって混合されてしまったとします。つまり、それぞれの画像の$i$番目の画素の値を並べたベクトルを
$$
x = (\mathrm{img}[0]_i, \mathrm{img}[1]_i, \mathrm{img}[2]_i)^\top
$$
として
$$
y = Ax
$$
と変換された$y$の要素を第$i$成分に持つような画像が観測として得られるとします。
この直交行列$A$がわからない時に混合されてしまった画像から元の画像を復元するという問題を考えます。つまり、ある直交行列$W$であって
$$
x = Wy = WAx
$$
つまり、$W = A^\top$となるような$W$を見つける問題です。もちろん何の仮定もなしに復元することはできないわけですが、今回は画像それぞれが独立な信号だと思って、いわゆる独立成分分析を行います。詳細は省きますが、目的関数として以下のような4次のモーメントを考えます。
$$
f(W) = \sum_{i=0}^3\sum_{j}\mathrm{img}[i]_j^4
$$
$A$は直交行列なので、$W$として考える行列も直交行列に限ってしまって良いでしょう。よって最適化問題としては、
$$
\min_{W:\text{直交行列}} f(W)
$$
と書くことができます。
リーマン多様体上の最適化
上で定義した問題は行列全体の空間(線型空間)で見れば制約付き最適化となります。しかし、そもそも直交行列しかいないような世界を考えれば制約なし最適化になるはずです。そうした直交行列からなる空間はStiefel多様体と呼ばれるリーマン多様体の一種になります。よって今回の問題をStiefel多様体上の最適化問題と考えれば、扱いやすい制約なし最適化として定式化できます。
manoptを使ってみる
実際にこの問題をPythonで解いてみましょう。manoptはMatlab, Python, Juliaで使えるリーマン多様体上の最適化のためのライブラリです。今回は手っ取り早くこれを使うことにします。詳細はgistをみてください。
まずコスト関数を定義します(observed_dataは画像を一次元化して並べたものです)。
def cost(W):
tmp = np.dot(W, observed_data)
res = (tmp**4).sum()
return res
これは自動微分できる必要があるので、import autograd.numpy as npをしておきましょう(torchも使えるらしいが動かなかった)。
次に多様体 (manifold) とソルバを定義します。今回は最急降下法を使うことにしました。manifoldはもちろんStiefel多様体です。
manifold = Stiefel(n, n)
problem = Problem(manifold = manifold, cost = cost, verbosity = 1)
solver = SteepestDescent()
あとはソルバを走らせるだけです。
W_opt = solver.solve(problem)
結果
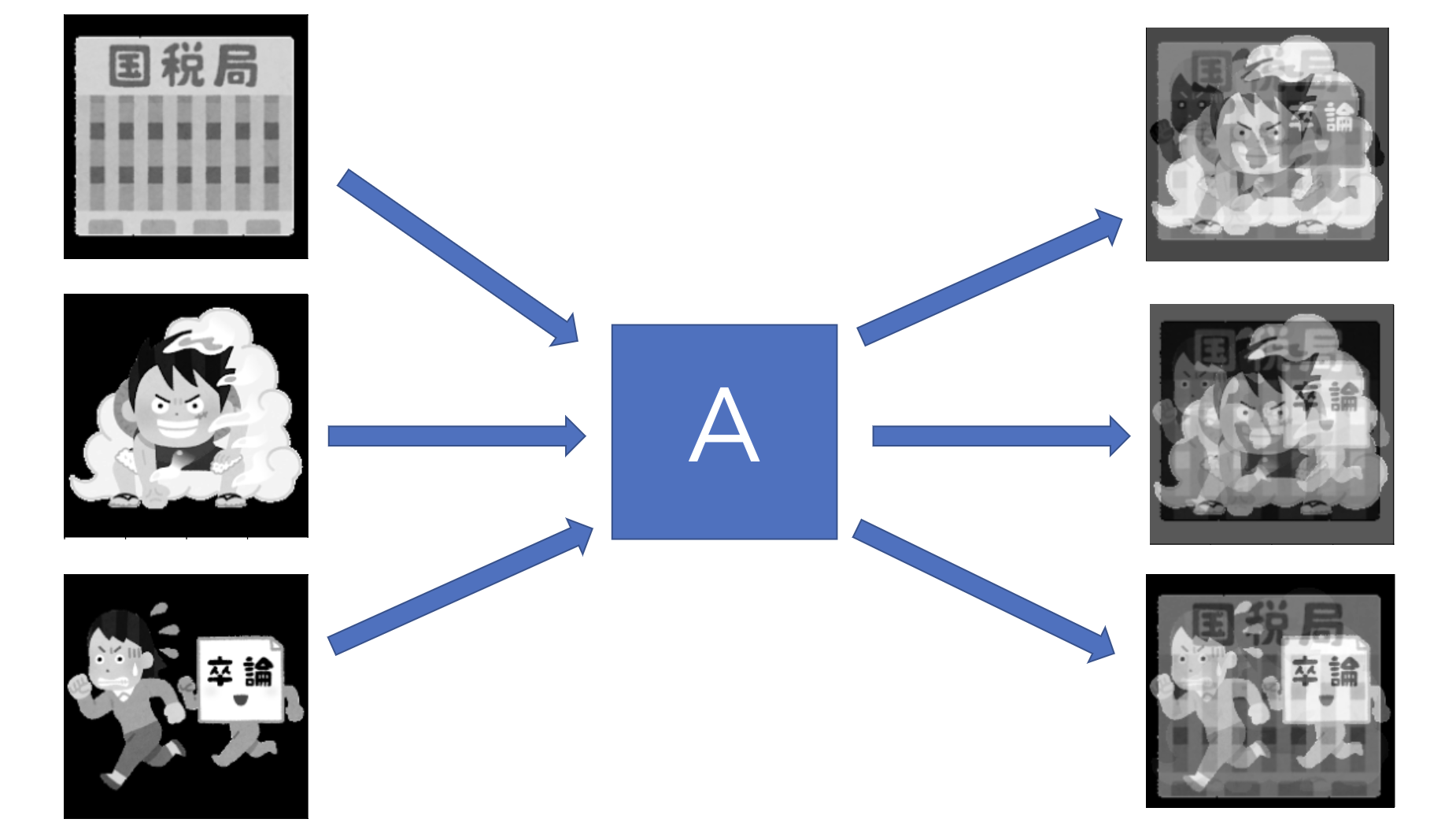
上で示したコードで得られた復元結果は以下のようになりました。
国税庁には少しルフィーが映り込んでしまっていますが、結構ちゃんと分離できていることがわかりますね。
内部で何をやっているのか?
線型空間上の通常の最急降下法と比較しながら、リーマン多様体上の最急降下法が何をしているかを確認しましょう。
通常の最急降下法では$\alpha$をstep sizeとして
$$
W_{i+1} = W_i - \alpha\nabla f(W_i)
$$
と暫定解$W_i$を更新します。$\nabla f(W_i)$は$W_i$における最急降下方向ということができます。実はリーマン多様体上の各点$W$には接空間が付随し、そこには内積$\langle\cdot, \cdot\rangle_W$が定められています。そこで、この接空間上で、$\langle\cdot, \cdot\rangle_W$に関する最急降下方向を$\operatorname{grad} f(W)$としましょう。するとリーマン多様体上の最急降下法はナイーブには以下のように書けると予想できます。
$$
W_{i+1} = W_i - \alpha\operatorname{grad} f(W_i)
$$
しかし、線型空間の場合とは違って、$W_i - \alpha\operatorname{grad} f(W_i)$が多様体に含まれているとは限りません。そこで、$W_i - \alpha\operatorname{grad} f(W_i)$を多様体に引き戻す(retraction)ことが必要になります。式で書けば、
$$
W_{i+1} = R_{W_i}(- \alpha\operatorname{grad} f(W_i))
$$
のようになります。$R_W$がretractionです。
今回の場合はQR分解を用いてretractionを定義します。つまり、$W_i - \alpha\operatorname{grad} f(W_i) = QR$($Q$: 直交行列、$R$: 上三角行列)という分解を考えたときの$Q$を$W_{i+1}$とします。
終わりに
いらすとやには何でもあることがわかりました。卒論からは逃げられない!
参考文献
金森 敬文・鈴木 大慈・竹内 一郎・佐藤 一誠: 機械学習のための連続最適化, 講談社(2016)