はじめに
古典的な計算機上で素因数分解をするには愚直には$O(\sqrt{N})$の計算量がかかり、現在開発されている最も効率的なアルゴリズムでも桁数の指数時間程度はかかってしまうようです。でも300桁レベルの素因数分解をしようと思うと、死ぬほど時間がかかってしまいます。え?多項式時間で素因数分解を?できらぁ!というのがショアのアルゴリズムです。この記事ではそのショアのアルゴリズムをqiskitで実装して、実際の量子コンピュータで実行するのがこの記事の目標です。今回は15を因数分解していきます。この記事にはおそらく(というか確実に)間違いや、誤植があると思うので、もし見つけたら優しく教えてください...
流れ
ショアのアルゴリズムを説明するには、いろいろ準備が必要なのですがまず全体の流れを書いておきたいと思います。
まず、素因数分解したい自然数$N$と互いに素な自然数$x$を考えます(互いに素かどうかはユークリッドの互除法で判定できます。)。以下modNの世界で考えることにします。$x^r = 1$となるような最小のrを位数と呼びます。この位数を求めることが素因数分解に有効であることが知られています。しかし古典的な計算機ではこの計算にも指数時間がかかってしまいます。これを解決するのが位相推定アルゴリズムです。位相推定アルゴリズムはユニタリ行列の固有値(絶対値は1)の位相を近似的に与えてくれます。$\mod N$の世界で$U^r = I$となるようなUを考えるとその固有値からrを求めることができるようになります。この位相推定アルゴリズムのサブルーチンとしてこのあと説明するアダマールテストと量子フーリエ変換が必要です。
アダマールテスト
まずアダマールテストと呼ばれるアルゴリズムを説明します。
アダマールテストは以下のような回路で実現されます($U$は任意のゲートです)。
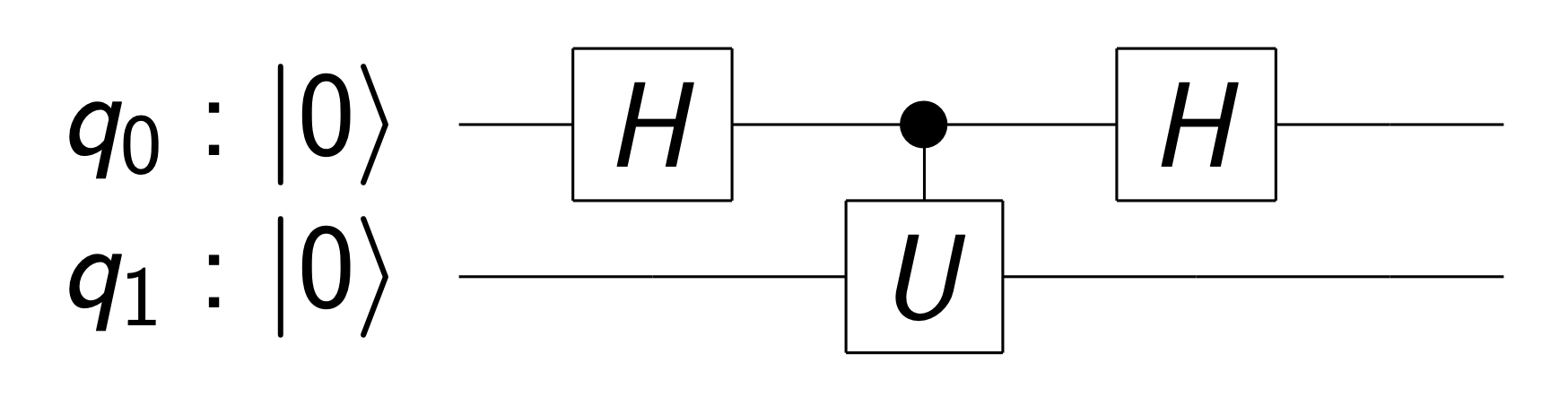
この回路に$q_0 = \left|0\right>, q_1 = \left|\varphi\right>$ を通すとどうなるか考えてみましょう。ただし$\left|\varphi\right>$は$U$の固有ベクトルであり、その固有値を$e^{i\lambda}$とします。
$$
\left|0\right>\left|\varphi\right>\rightarrow \frac{1}{\sqrt{2}}(\left|0\right>\left|\varphi\right>+\left|1\right>\left|\varphi\right>)\rightarrow
\frac{1}{\sqrt{2}}(\left|0\right>\left|\varphi\right>+e^{i\lambda}\left|1\right>\left|\varphi\right>)\rightarrow
\left(\frac{1+e^{i\lambda}}{2}\left|0\right>+\frac{1-e^{i\lambda}}{2}\left|1\right>\right)\otimes\left|\varphi\right>
$$
control-Uゲートを通過した後の量子ビットは$\frac{1}{\sqrt{2}}(\left|0\right>+e^{i\lambda}\left|1\right>)\otimes \left|\varphi\right>$という状態になります。Uの固有値の位相が前(第一量子ビット)に位相として出てきているのがわかると思います。そこにさらにアダマールゲートを作用させることで、第一量子ビットの観測確率としてUの固有値の位相を得ることができます。コントロールビットにはなんの操作もしていないのに、まるで2番目の量子ビットから位相が乗り移ったかのように観測確率が変化するのは不思議ですね。ただし、この方法で固有値の位相を知ろうとすると何度も測定しなければなりません。この問題点を解決するアルゴリズムとして位相推定アルゴリズムが出てくることになります。
量子フーリエ変換
量子フーリエ変換は離散フーリエ変換を行うアルゴリズムです。数列の長さを$2^n$とすると、古典計算機ではみんな大好き高速フーリエ変換で離散フーリエ変換を$O(n2^n)$で行うことができますが、量子フーリエ変換では$O(n^2)$という$n$の多項式時間で解くことができます!
まず、離散フーリエ変換の定義式を思い出してみましょう。
$$
y_k = \frac{1}{\sqrt{2^n}} \sum_{j=0}^{2^n-1} x_j e^{i\frac{2\pi kj}{2^n}}
$$
これをqubit上で表現すると、
$$
|x\rangle = \sum_{j=0}^{2^n-1} x_j |j\rangle \rightarrow |y\rangle = \sum_{k = 0}^{2^n-1} y_k |k\rangle \
|j\rangle \rightarrow \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{i\frac{2\pi jk}{2^n}}|k\rangle
$$
となります。
実はこの変換はunitaryであり、量子コンピュータはユニバーサルゲートセットによって任意のユニタリ変換を近似できるので、この変換は量子コンピュータ上で実現可能です。しかし、このままではどのようなゲートを噛ませればいいのかわからないのでもっと使いやすい形に変形したいと思います。kを二進数で展開していろいろ頑張ると以下のようになります。
$$
|j\rangle \rightarrow\otimes_{l = 1}^{2^n} (|0\rangle+e^{\frac{2\pi i}{2^l}}|1\rangle)
$$
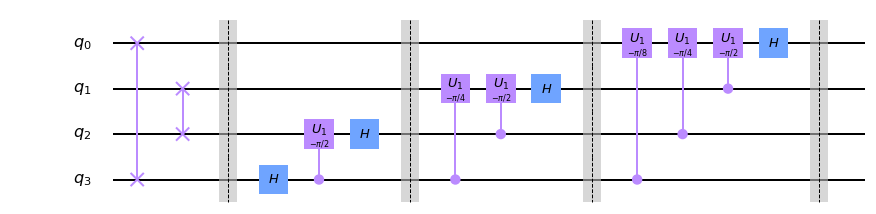
この形にすると、それぞれのq-bitのテンソル積としてかけているので、フーリエ変換がアダマールゲートと回転ゲートにより、実現できることがわかると思います(下図)。
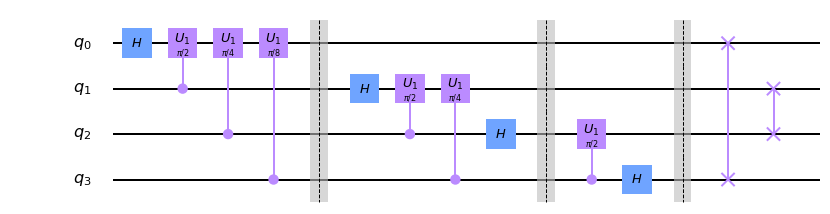
実はショアのアルゴリズムではその逆変換である逆量子フーリエ変換を使うのでこれも下に示しておきます。これはただゲートを反対からかけていっただけです(ただし回転は逆回転)。
ところで量子ビットの読む方向には注意が必要です。ここではq0q1q2q3の順に読むことにします。つまり、$q0 = 1, q1 = q2 = q3 = 0$なら$x = 1000(2) = 8$です。
一応ゲートの説明もしておくと、Hはアダマールゲート、U1はRzゲートと同じで、$|1\rangle$にのみ$e^{i\theta}$の位相をつけるゲートです。詳しくはこちら
位相推定アルゴリズム
位相アルゴリズムはアダマールテストを改良したようなアルゴリズムとなっています。
サイズ$2^n$のユニタリ行列$U$の固有値を$e^{2\pi i\lambda}$, それに対応する固有ベクトルを$|\varphi\rangle$とします。もし、$\lambda$が二進法で$m$桁の小数で表すことができ、
$$
|y\rangle = \frac{1}{\sqrt{2^n}}\sum_{k = 0}^{2^m-1}e^{2\pi ij\lambda}|j\rangle
$$
という状態を作り出すことができれば、逆離散フーリエ展開で$\lambda$がわかります(前章の定義式と見比べてみてください)。
位相推定アルゴリズムにはm+n個の量子ビットを使い、入力には$|0\rangle|\varphi\rangle$を入れることにします。まずアダマールゲートを最初のm個の量子ビットに適用することで$|0\rangle$から$|2^m-1\rangle$までの重ね合わせ状態を作ります。次に$i$の$k$桁目が1ならば後ろの$|\varphi\rangle$に$U^k$をかけます。するとアダマールテストと同じ原理で$|i\rangle\rightarrow e^{2\pi ik\lambda}|i\rangle$になります。これを$k = 1, 2, \cdots m$で繰り返すことで、上位mビットに上の状態を実現することができます!(jを二進数で考えてみてください)回路図は下のようになります。回路図を見た方がわかりやすいかもしれません。

素因数分解への応用
なぜ、位数rが求まると、素因数分解できるのでしょうか?まず、rは偶数であると仮定します(ランダムに取るといい確率で偶数になってくれるらしいです)。すると以下のような変形ができます。
$$
x^r = 1 \mod N\
(x^{r/2}-1)(x^{r/2}+1) = 0\mod N
$$
つまり、$(x^{r/2}-1)$と$(x^{r/2}+1)$のどちらかはNと非自明な公約数を持つことになります。どちらもがN の倍数となってしまう確率は低いです。公約数はユークリッドの互助法によって、古典計算機で高速に計算できます。そこで$U^r = I$なる行列を作りたいのですが、これは簡単で、$U|i\rangle = |i\cdot x \mod N\rangle$となるように定義すれば良いです。ただし$i\geq N$については何もしないことにします。実はこれもユニタリ行列であることが示せます。これに位相推定アルゴリズムを用いれば位数rが十分な確率で求まります。一つ問題があるのは、位相推定アルゴリズムでは、固有ベクトルを利用していましたが、今回はわかりません。しかし、入力としては$\left|1\right>$を用いれば十分です。なぜなら、固有ベクトルで展開すれば、位相推定アルゴリズムで得られる値は固有値のどれかであり、そのどれであっても$s/r (s = 0, 1, \dots r-1)$という形で表せるため、連分数アルゴリズムによってrを高速に求められるからです($s = 0$の場合は無視します)。連分数アルゴリズムは小数を連分数で近似することでもっともらしい分数としての形を推定します。詳しいことはcontinued fraction algorithmでググりましょう。一応実装は後に載せてあります。
Qiskitでの実装
さて、ここからが本番です。上で見てきたアルゴリズムをシュミレーターで実行して$N = 15$を$x = 4$で因数分解してみましょう。今回はqiskitという量子計算ライブラリを使います。qiskitについて詳しくは公式ドキュメントを参照してください。実行は全てjupyter notebook上で行なっています。
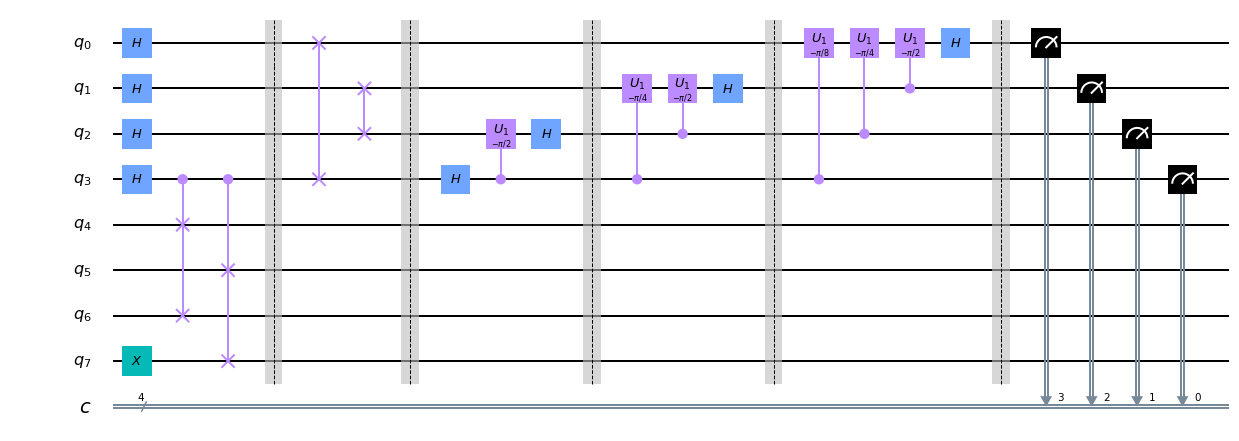
量子コンピュター部分は以下のようになります。前章で出てきたUの実装ですが、一般の剰余演算を実装するのは困難なので、$N = 15, x = 4$という事実を活用してしまっています(${U}^{2^i}$については位数が2であることも使ってしまってい省略しています...)が、まあ今回は雰囲気を掴むだけなのでいいでしょう。
from qiskit import *
from qiskit.providers.ibmq import least_busy
from qiskit.visualization import plot_histogram
from qiskit.tools.monitor import job_monitor
import math
q = QuantumRegister(8, "q")
c = ClassicalRegister(4, "c")
circuit = QuantumCircuit(q, c)
circuit.x(7)
# Hadamard transform
for i in range(4):
circuit.h(i)
# U4^1 gate
circuit.cswap(3, 4, 6)
circuit.cswap(3, 5, 7)
circuit.barrier()
# U4^2 gate
# U4^4 gate
# U4^8 gate
circuit.barrier()
# inverse quantum Fourier transform
circuit.swap(0, 3)
circuit.swap(1, 2)
circuit.h(3)
circuit.cu1(-np.pi/2, 3, 2)
circuit.h(2)
circuit.barrier()
circuit.cu1(-np.pi/4, 3, 1)
circuit.cu1(-np.pi/2, 2, 1)
circuit.h(1)
circuit.barrier()
circuit.cu1(-np.pi/8, 3, 0)
circuit.cu1(-np.pi/4, 2, 0)
circuit.cu1(-np.pi/2, 1, 0)
circuit.h(0)
circuit.barrier()
# measure
for i in range(4):
circuit.measure(q[i], c[3-i])#二進法でx = q1q2q3q4になるようにしている
circuit.draw(output='mpl')
さて、あとは古典計算の部分です。連分数展開は以下のように実装しました(結構適当に書いてちょっとサンプル試しただけなのでかなり怪しいですが...)。相対誤差がeps以下になったら終了するようにしています。
eps = 0.01
def continued_fractions_algorithm(x):
res = [int(x)]
x-=int(x)
if x/(res[0]+0.1)>eps:
a = continued_fractions_algorithm(1/x)
res+=a
return res
eps = 0.01
def continued_fractions_algorithm(x):
res = [int(x)]
x-=int(x)
if x/(res[0]+0.1)>eps:
a = continued_fractions_algorithm(1/x)
res+=a
return res
さて、ここで(量子計算機としての)計算量を見積もりましょう。素因数分解したい自然数が$n$bitであるとして、離散フーリエ変換パートが $O(n^2)$、位相推定アルゴリズムパートが$O(n^3)$です。古典パートはボトルネックとならないので、全体で$O(n^3)$の多項式時間で解くことができました!
あとは以下のコードを実行すると、
def shor_algorithm(use_simulator):
if use_simulator:
backend = BasicAer.get_backend('qasm_simulator')
else:
backend = IBMQ.get_provider().get_backend('ibmq_16_melbourne')
flag = False
job = execute(circuit, backend, shots = N)
job_monitor(job)
result = job.result()
counts = result.get_counts(circuit)
measures = np.array(list(map(lambda x:int(x, 2), counts.keys())), dtype = np.int64)
probs = np.array(list(counts.values()))/N
for i in range(5):
output = np.random.choice(measures, p = probs)
a = continued_fractions_algorithm(output/2**4)
r , s =1, a[-1]
for i in range(len(a)-1)[::-1]:
r, s = s, a[i]*s+r
if r % 15 == 0 or s == 0:
continue
d = math.gcd(15, 4**(r-1)-1)
if d != 1:
flag = True
break
plot_histogram(result.get_counts())
if flag:
print('{0} devides 15 with r = {1}'.format(d, r))
else:
print('the algorithm failed')
return result
%matplotlib inline
use_simulator = True
result = shor_algorithm(use_simulator)
plot_histogram(result.get_counts())

となり、因数分解に成功しました!
実機での計算
qiskitから無料で使える量子コンピューターであるIBMQを操作することができます。公式ページはこちら。操作にはアカウント作成が必要です。
まず以下のコードを実行しておきます。
from qiskit import IBMQ
my_token = ""
IBMQ.save_account(my_token)
provider = IBMQ.load_account()
my_tokenのところには公式ページのMy Accountのところから取得したトークンを入れてください。
今回は8qubit使っているのでibmq_16_melbourneを使います。少し時間がかかりますが、上のコードでuse_simulator = Falseとして実行すると、

あれっ?
まとめ
いかがでしたか?今回量子コンピュータによる因数分解を試したわけですが、前の章でみてきた通り実機だとかなり誤差があります。もちろん今回は誰でも使えるもの簡易的なもので試しているわけですが、15の因数分解にすら手こずるとなると量子コンピュータが実用化されるには時間がかかりそうですね...。
参考
Quantum Native Dojo https://dojo.qulacs.org/ja/latest/
宮野健二郎,古澤明, 量子コンピュータ入門 日本評論社 2016
Michael A. Nilsen,Isaac L. Chuang Quantum Computation and Quantum Information 10th Anniversary Edition 2010