初めてのJulia

はじめに

この記事はJuliaに入門して数日の素人が書いたものなのであまり鵜呑みにしないでください. 環境構築はこの記事に色々まとまっているので参考にさせていただきました.

Juliaの導入

Mac環境で話を進めます.
公式サイトからdmgファイルをダウンロードしてここに書いてあるようにやれば終わりです. 簡単！ ちなみにjupyterでも使えます. 詳しくは上の参考記事をみてください. 以下はjupyter上で実行しています.

Juliaで半円則を実証

ものは試しということでJuliaでウィグナーの半円則を実証してみようと思います.
半円則についてはこちら
ようは対称ランダム行列の固有値分布が半円型になるというものです.
まずはランダム行列を作りましょう. 今回は行列のサイズを$size=10000$としました.
Juliaでは各要素が標準正規分布に従う行列はrandn関数を用いて作ることができます.

using Plots
using LinearAlgebra
size = 10000
mat=randn(Float32, size, size)

これだと対称行列になっていないので, 普通にfor文を用いて対称行列にしました.

for i in 1:size
    for j in i+1:size
        mat[i, j]=mat[j, i]
    end
end

あとは固有値を求めるだけです. LinearAlgebraのなかにeigvals関数があるので,

@time eigenvalues = eigvals(mat)

とします. @.timeは実行時間を測ってくれるマクロです. 僕の環境では約40sでした.
最後に固有値のヒストグラムを書きましょう. これはPlotsの中のhistogram関数でできます.

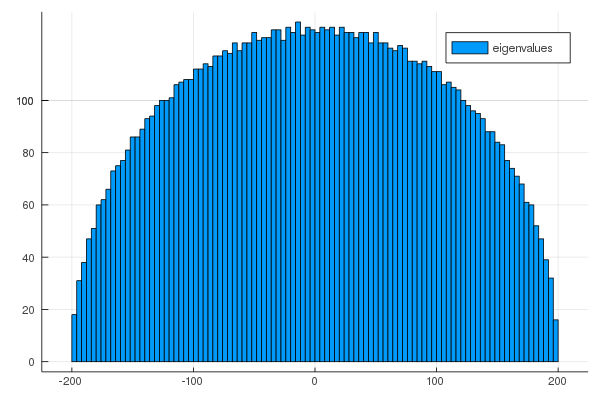
histogram(eigenvalues, bins = range(-200, 200, step=4), label="eigenvalues")

綺麗な半円が見えました！

終わりに

JuliaはPythonライクに書けて非常に使いやすくていいと思います. Pythonとの差別化ポイントは実行速度だと思うのですが, 今回はほぼライブラリを使っただけなのであまり速度差はなさそうです...と思ったのですが, np.linalg.eigvalsでやってみたところ死ぬほど時間がかかりました...ということでjuliaすごい！ あと最初に実行するときはかなり時間がかかったりしますが大体二回目以降は高速になるので大丈夫です.