11/8(Thu)輪読会資料 @ Yahoo Lodge
基本的な説明は、別資料で実施
メインは、範囲内の演習問題を解いていくことで、
教科書の内容をなぞっていく形式とする。
1.1
担当外のため省略
1.2
担当外のため省略
1.3 (標準)
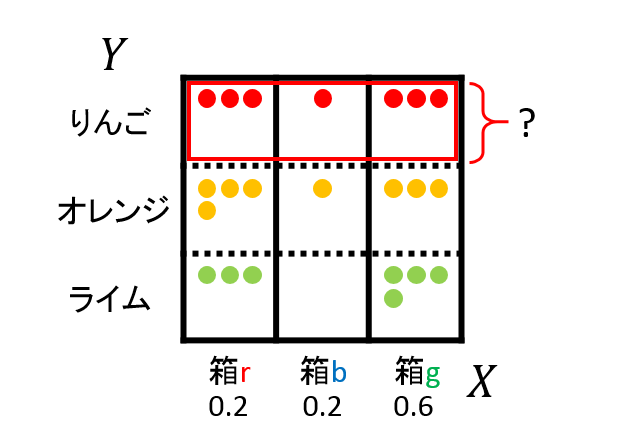
問題文
3個の色分けされた箱r(赤)、b(青)、g(緑)を考える。
箱rには、3個のりんご、4個のオレンジ、3個のライム
箱bには、1個のりんご、1個のオレンジ、0個のライム
箱gには、3個のりんご、3個のオレンジ、4個のライムが入っている。
この箱を$P(r)=0.2 、 P(b)=0.2 、 P(g)=0.6$という確率でランダムに選び、果物を箱から1個取り出す。
箱の中の果物は、等確率で選ばれるとする時、りんごを選び出す確率を求めよ。
また、選んだ果物がオレンジであったとき、それが緑の箱から取り出されたものである確率はいくらか?
前提知識
確率の基本法則
加法定理
$p(X) = \sum_{Y}p(X,Y)$
乗法定理
$p(X,Y) = p(Y|X)p(X)$
同時確率の対称性
$p(X,Y) = p(Y,X)$
それぞれを展開し、両辺を$p(X)$で割ると、ベイズの定理が導ける
$p(Y|X)p(X) = p(X|Y)p(Y)$
$p(Y|X) = \frac{p(X|Y)p(Y)}{p(X)}$
解説
確率の基本法則(加法・乗法定理)に従うと、
果物 $(X)$ を箱 $(Y)$ から1個取り出すとき、
りんご $(X=A)$ を選び出す確率 $P(X=A)$は、以下の通り
\begin{align}
p(X=A) &= \sum_{Y}^{r,b,g}p(A,Y) = \sum_{Y}^{r,b,g}p(A|Y)p(Y) \\
&= p(A|r)p(r)+p(A|b)p(b)+p(A|g)p(g)\\
&=\frac{3}{10}\frac{1}{5}+\frac{1}{2}\frac{1}{5}+\frac{3}{10}\frac{3}{5} \\
&= \frac{17}{50} \\
\end{align}
また、選んだ果物 $(X)$ がオレンジ $(X=O)$ であったとき、
それが緑の箱 $(Y=g)$ であるときの確率 $p(g|O)$ は、以下の通り
\begin{align}
p(g|O) &= \frac{p(O|g)p(g)}{p(O)}\\
&= \frac{\frac{3}{10}\frac{3}{5}}{\frac{18}{50}}\\
&= \frac{1}{2}
\end{align}
1.4 (標準)
問題文
連続変数 $x$ 上で定義された確率密度 $p_x(x)$ を考える。
$x=g(y)$ により非線形変換を施すと、密度は以下の変換を受ける。
\begin{align}
p_y(y) &= p_x(x)\left|\frac{dx}{dy}\right|\\
&= p_x(g(y))|g^{\prime}(y)|\\
\end{align}
上記を微分して、$y$ に関する密度を最大にする位置 $\hat{y}$ と、 $x$ に関する密度を最大にする位置 $\hat{x}$ とが、ヤコビ因子の影響によリ、ー般には単純な $\hat{x} = g(\hat{y})$ という関係にないことを示せ。
これは、確率密度の最大値が、(通常の関数と異なり)変数の選択に依存することを示している。
線形変換の場合には、最大値の位置が変数自身と同じ変換を受けることを確かめよ。
前提知識
離散的な事象:くじ引きでx等が当たる。コイントスで裏がでる。
確率は「事象と標本空間の比」
連続的な事象:投げたダーツが中心からxセンチの位置に当たる。
確率は「対象区間内の確率密度関数の積分値」
\int_a^bp(x)dx
非線形変換、ヤコビ因子
※ホワイトボードで説明します。
解説
両辺を$y$ で微分すると、(合成関数の微分)
\begin{align}
\frac{dp_y(y)}{dy} &= \frac{d}{dy}(p_x(g(y))|g^{\prime}(y)|)\\
&= \frac{d(p_x(g(y))}{dy}|g^{\prime}(y)|+p_x(g(y))|g^{\prime\prime}(y)|\\
&= p^{\prime}_x(g(y))g^{\prime}(y)|g^{\prime}(y)|+p_x(g(y))|g^{\prime\prime}(y)|\\
\end{align}
yに関する密度$P_y(y)$を最大にする位置 $y=\hat{y}$ の時 (yで微分して $P^{\prime}_y(\hat{y})=0$ を満たす $\hat{y}$ )
\frac{dp_y(y)}{dy}|_\hat{y} = 0
であるから
p^{\prime}_x(g(\hat{y}))g^{\prime}(\hat{y})|g^{\prime}(\hat{y})|+p_x(g(\hat{y}))|g^{\prime\prime}(\hat{y})|=0
ここで、$\hat{x}=g(\hat{y})$ と仮定すると (背理法)
p^{\prime}_x(\hat{x})g^{\prime}(\hat{y})|g^{\prime}(\hat{y})|+p_x(\hat{x})|g^{\prime\prime}(\hat{y})|=0
となるが、 $x=\hat{x}$ は、密度$P_x(x)$を最大にする位置であるため、
p^{\prime}_x(\hat{x}) = 0
すなわち、第一項は0となる。
ただし、第二項の$g(y)$が非線形変換(二次以上)であるから、$g^{\prime\prime}(\hat{y})\neq0$
さらに、題意より、$p_x(\hat{x})$は最大値をとらなければならない。
最大値が0の場合、確率密度の定義を満たさない(常に0以上かつ、全確率は1)ため、
\hat{x}\neq g(\hat{y})
しかし、$x=g(y)$が線形変換(一次以下)である場合、第二項も0となり、
$y=\hat{y}$ のとき、最大値の位置が変数と同じ変換を受けていることが確認できた。
1.5 (基本)
問題文
$var[f]=E[(f(x)-E[f(x)])^2]$
であるとき、以下で表せることを確かめよ。
$var[f]=E[(f(x)^2]-E[f(x)]^2$
前提知識
期待値の定義(ある関数$f(x)$の確率密度$p(x)$の元での平均値)
$E[f(x)]=\int_{-\infty}^{\infty}f(x)p(x)dx$
a,bが定数の場合、以下のような性質を持つ
$E[af(x)+b]=aE[f(x)]+b$
解説
$E[f(x)]=\int_{-\infty}^{\infty}f(x)p(x)dx$ が定数であることを視覚的にも明瞭にするために、逐次、$\mu$に置き換える
\begin{align}
var(f) &= E[(f(x)-E[f(x)])^2]\\
&= E[(f(x)-\mu)^2]\\
&= E[f(x)^2-2\mu f(x)+\mu^2]\\
&= E[f(x)^2]+E[-2\mu f(x)]+E[\mu^2]]\\
&= E[f(x)^2]-2\mu^2+\mu^2 E[1]]\\
&= E[f(x)^2]-E[f(x)]^2
\end{align}
1.6 (基本)
問題文
2つの変数 $x$、$y$ が独立なら、それらの共分散は0になることを示せ。
前提知識
連続型2変数X,Yの確率密度$f_{XY}(x,y)$に関して、$g(X,Y)$の期待値$E[g(X,Y)]$は以下の通り
E[g(X,Y)]=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x, y)f_{XY}(x,y)dxdy
Xの期待値$E[X]$は、
\begin{align}
E[X]&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{XY}(x,y)dxdy\\\
&=\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}f_{XY}(x,y)dydx\\\
&=\int_{-\infty}^{\infty}xf_{X}(x)dx\\\
\end{align}
共分散は、
\begin{align}
\sigma_{XY}&=C[X,Y]=E[(X-\mu_X)(Y-\mu_Y)]\\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(x-\mu_X)(y-\mu_Y)f_{XY}(x,y)dxdy\\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(xy-x\mu_Y-y\mu_X+\mu_X\mu_Y)f_{XY}(x,y)dxdy\\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_{XY}(x,y)dxdy-\mu_X\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}yf_{XY}(x,y)dxdy-\mu_Y\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{XY}(x,y)dxdy+\mu_X\mu_Y\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{XY}(x,y)dxdy\\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_{XY}(x,y)dxdy-\mu_X\mu_Y-\mu_Y\mu_X+\mu_X\mu_Y\\\
&=E[XY]-\mu_X\mu_Y=E[XY]-E[X]E[Y]\\\
\end{align}
解説
\begin{align}
E[XY]&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_{XY}(x,y)dxdy\\\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X}(x)yf_{Y}(y)dxdy\\\
&=\int_{-\infty}^{\infty}xf_{X}(x)dx\int_{-\infty}^{\infty}yf_{Y}(y)dy=E[X]E[Y]\\\
\sigma_{XY}&=E[XY]-E[X]E[Y]=0\\\
\end{align}