主成分分析とは
あの子の趣味はなんだろう。好きなものはなんだろう。特徴はなんだろう。構成成分はなんだろう。
誰もが一度は抱いたことのある疑問です。これを機械学習では
あの子の主成分はなんだろう
なんて言ったりします。今度使ってみてください。
さて、データを機械学習していく上で、そのデータの特徴が上手く表せていないと精度がイマイチです。
そこで、雑多な成分を排除して一番特徴となる成分だけを上手く抽出しようというのが主成分分析というわけです。
次元削減なんて言われ方もしますがほとんど同じ意味です。
主成分分析のアルゴリズム
主成分分析のアルゴリズムには主にPCA法が用いられます。
PCAと調べるとモルヒネだのアンフェタミンだの会計ソフトだのいろいろ出てきますが機械学習ではPrincipal Component AnalysisのPCAを指します。当然ですが和訳すると「主成分分析」です。
概要
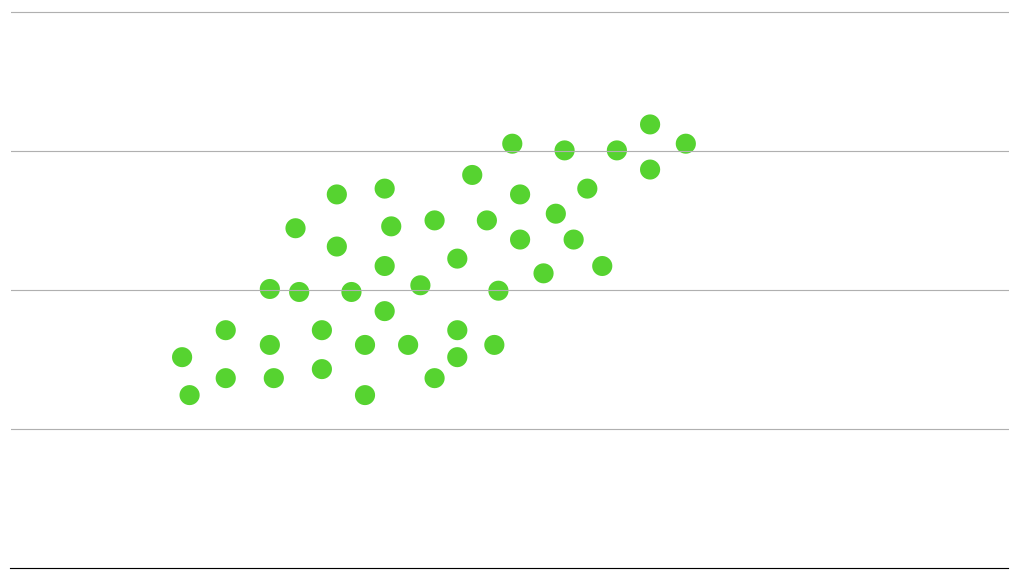
例えば2次元のプロットがあったとしますね。
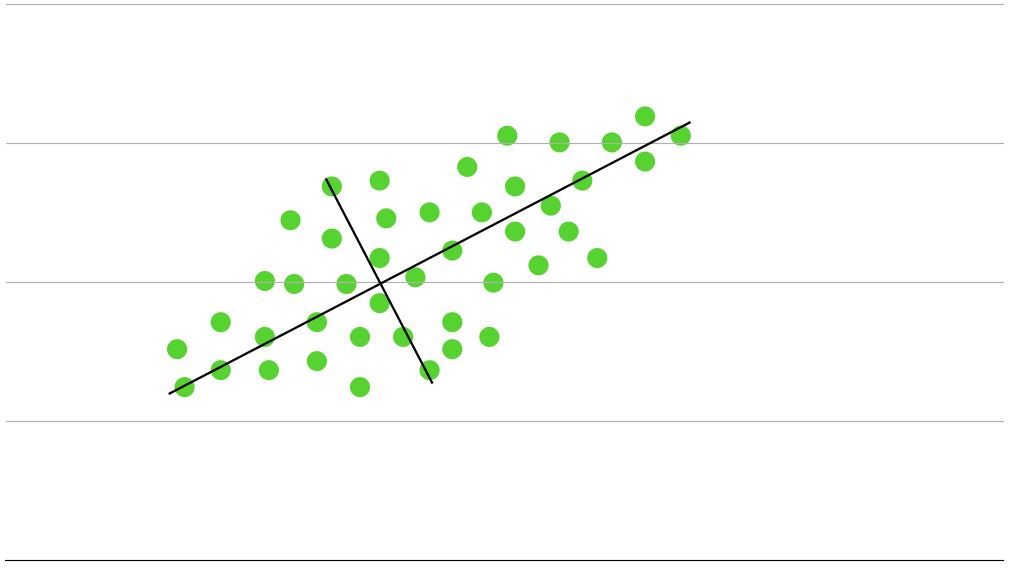
PCAは特徴を説明することなので、一番この特徴を説明している2本の直交した直線を引きます。
イメージで言うとこんな感じです。次元の数だけ直線が引けることがわかると思います。
雰囲気は掴めましたか?ここから少し難しいお話になります。
分散
さて、さっきの2本の線分はデータの分散を表していることは見てわかると思います。
そして、分散の大きいものほどデータを説明していることがわかると思います。
この分散を定式化するとこのようになります。(分散の公式より)
$$
\mu^n = a_1x_1^n + a_2x_2^n + ... + a_px_p^n
$$
すると、分散$\mu$の平均は
$$
\overline{\mu} = \frac{1}{N}\sum_{n=1}^{N}(a_1x_1^n + a_2x_2^n + ... + a_px_p^n) = a_1\overline{x_1} + a_2\overline{x_2} + ... + a_p\overline{x_p}
$$
となることがわかりますね。わかりますよね?
実はこっからまたゴニョゴニョするのですが、要は分散の分散を求めます。すると
$$
s_{\mu}^2 = \frac{1}{N}\sum_{n=1}^{N}(\mu^n - \bar{\mu})^2= {\bf{a}^T}S \bf{a}
$$
となります。これを最大化することで主成分分析が完了します。
ラグランジュの未定乗数法
機械学習が大好きなみなさんは数学も大好きな筈なのでさすがにこの単語は聞いたことくらいあるでしょう。
まず、これを説明する前に最小化・最大化という言葉がちらついたら微分(偏微分)が頭にくるようにしなければなりません。
関数の極値を求めるにはその導関数(偏導関数)を調べればよい、というのは高校数学でもやりましたよね。
さて、ラグランジュの未定乗数法とは、
ある条件下での任意の関数の極値を求める手法
です。詳しいラグランジュの未定乗数法による極値の解法は書籍などで勉強するのが良いと思われます。
さて、今回ならば、$a_1^2 + a_2^2 + ... + a_p^2 = 1$という条件下のもと$s_u^2 = {\bf{a}^T}S\bf{a}$の極値を求めることにあたります。
$$
L(a, \lambda) = {\bf{a}^T}S{\bf{a}}-\lambda({\bf{a}^T\bf{a}}-1)
$$
この偏導関数は、
$$
\frac{dL}{d\bf{a}} = (S + S^T){\bf{a}} - 2\lambda{\bf{a}} = 2S{\bf{a}} - 2\lambda{\bf{a}} = 0
$$
これを解くと、
$$
S{\bf{a}} = \lambda{\bf{a}}
$$
さて、これによって、次のことを証明することができました。
データセットの分散共分散行列Sの固有ベクトルが$\bf{a}$, 固有値が$\mu$の分散$s_{\mu}^2$と一致する
つまりは、分散共分散行列の固有値問題を解くことが主成分分析のアルゴリズムです。
さて、ここからは統計の知識となりますが、実は分散共分散行列は、標準化された相関行列と同じ性質を持ちます。相関行列は対称行列となるため、そちらの方が都合がよく、そちらを用いる場合が多いので今回はそちらについて見ていきましょう。
アルゴリズム
アルゴリズムをまとめます。
- データを標準化します
- 相関行列を計算します
- 相関行列の固有値問題を解きます
- 固有値の大きい方から対応する固有ベクトルを並べます
- この内、ベクトルk個(k≥0)を選択することによって次元を圧縮することができます
- k個の固有ベクトルから特徴変換行列Wを作成します
- XとWの積が主成分となります
実装
実装はめちゃくちゃ簡単です。numpyを使えばチョチョイのチョイです。多分コメントアウトを見れば一発で理解できると思うのでドンと載せちゃいます。
import numpy as np
def pca(X):
# 標準化
X = (X - X.mean(axis=0)) / X.std(axis=0)
# 相関行列
R = np.corrcoef(X.T)
# 固有値分解
eigen_values, eigen_vectors = np.linalg.eigh(R)
# 特徴変換
X_pca = X.dot(eigen_vectors)
return X_pca