前回は既に学習済みのパラメータがあるものとして、そこからフォワード計算を行ない予測を出すところを実装しました。今回は、データからパラメータを学習するところの実装について考えてみます。具体的には、「ゼロから作るDeep Learning」の5章にある、計算グラフベースでの誤差逆伝搬法の実装と、それを使った隠れ層二層のニューラルネットの学習と予測について書こうと思います。
一応Githubにレポジトリ作りました(まだあまり整理されていない)。ちなみに処理系はSBCL 1.4.3で動作確認しています。
https://github.com/masatoi/cl-zerodl
インストール手順は上記を参照してください。
準備
前回と同様に必要ライブラリを読み込み、作業用パッケージを定義しておきます。
metabang-bindは分配束縛などに対応したletの拡張版のような構文を導入するライブラリです。
cl-libsvm-formatはlibsvm形式のデータファイルを高速に読み込むための自作ライブラリです。MNISTを読み込むのに使用します。最近Quicklispに登録されたので、もしロードがうまくいかなければQuicklispをアップデートしてみてください。
(ql:quickload '(:mgl-mat ; 行列演算ライブラリ
:metabang-bind ; 分配束縛などのための構文ライブラリ
:cl-libsvm-format)) ; libsvm形式データのリーダ
(defpackage cl-zerodl
(:use :cl :mgl-mat :metabang.bind)
(:nicknames :zerodl))
(in-package :zerodl)
次に、defclassをラップするマクロdefine-classを定義しておきます。スロット名だけを指定すればそこからアクセサ名などを勝手につけてくれるのでタイプ量が減ります。なお、スロット名がアクセサ名になります。
(defmacro define-class (class-name superclass-list &body body)
`(defclass ,class-name (,@superclass-list)
,(mapcar (lambda (slot)
(let* ((slot-symbol (if (listp slot) (car slot) slot))
(slot-name (symbol-name slot-symbol))
(slot-initval (if (listp slot) (cadr slot) nil)))
(list slot-symbol
:accessor (intern slot-name)
:initarg (intern slot-name :keyword)
:initform slot-initval)))
body)))
;; 使用例
(define-class クラス1 (親クラス1 親クラス2)
スロット1
スロット2
(スロット3 初期値))
次に、いくつかスペシャル変数を設定しておきます。
*default-mat-ctype*と*cuda-enabled*は前回も出てきましたが、行列のデフォルトの数値型と、CUDAを有効化するかどうかのフラグです。
*print-mat*はREPLなどで行列を評価したときにその中身を表示するかどうかを制御します。*print-length*や*print-level*はリストや行列などを表示するときの最大長とネストレベルを制御します。これらは巨大な行列をうっかり評価してしまってREPLが落ちるのを防ぐために使います。
(setf *default-mat-ctype* :float ; 行列のデフォルトの数値型
*cuda-enabled* t ; CUDAを有効化するかどうか
*print-mat* t ; 行列の中身をprintするかどうか
*print-length* 100 ; 行列などを途中まで表示
*print-level* 10) ; ネストレベルの最大値
5.4 単純なレイヤーの実装
さて、この節では、乗算レイヤと加算レイヤを定義していきます。これらはニューラルネットの定義には直接関わらないのですが、レイヤの役割を示すための例として出てきているようです。
まずレイヤの親クラスを定義しておきます。すべてのレイヤは入出力を持つので、それらの次元数と入出力の値を保存する行列を持たせることとします。
(define-class layer ()
input-dimensions output-dimensions ; 入出力の次元数
forward-out backward-out) ; 入出力の値を保持する行列
layerを継承するクラスは順伝搬を行うforwardメソッドと逆伝搬を行うbackwardメソッドを持ちます。
5.4.1 乗算レイヤの実装
まずはlayerを継承するクラスmultiple-layerを定義します。ここでオブジェクトのスロットにxとyを追加しています。乗算レイヤは、順伝搬において2つの入力を取ってその要素積を出力する働きをしますが、その際に入力の値をxとyに保存しておき、逆伝搬時に使います。
次に、コンストラクタ関数make-multiple-layerを定義してます。この関数の中でスロットの初期値を指定しますが、ここで行列の領域を確保しておき、以降ではこれらの行列の内容を破壊的に書き換えていきます。
(define-class multiple-layer (layer)
x y)
(defun make-multiple-layer (input-dimensions)
(make-instance 'multiple-layer
:input-dimensions input-dimensions
:output-dimensions input-dimensions
:forward-out (make-mat input-dimensions)
:backward-out (list (make-mat input-dimensions) ; dx
(make-mat input-dimensions)) ; dy
:x (make-mat input-dimensions)
:y (make-mat input-dimensions)))
forwardメソッドでは前回出てきた行列積を計算するgemm!によく似たgeem!という関数を使っていますが、gemm!が行列積だったのに対してgeem!は要素ごとの積を計算します。
backwardメソッドでは、逆伝搬の入力doutに順伝搬時に保存したxとyを掛け、出力先をひっくり返します。
(defmethod forward ((layer multiple-layer) &rest inputs)
(bind ((out (forward-out layer))
((x y) inputs))
(copy! x (x layer))
(copy! y (y layer))
;; geem!は要素ごとの積
(geem! 1.0 x y 0.0 out)))
(defmethod backward ((layer multiple-layer) dout)
(let* ((out (backward-out layer))
(dx (car out))
(dy (cadr out)))
(geem! 1.0 dout (y layer) 0.0 dx)
(geem! 1.0 dout (x layer) 0.0 dy)
out))
forwardの定義中にbindというmetabang-bindパッケージで導入される構文が出てきています。これはletなどと同様に局所変数を束縛する構文なのですが、多値やリストからの分配束縛もできるようになっています。乗算レイヤのforwardは2つの値を取るので、inputsは2要素のリストとなっており、それぞれをxとyに束縛しています。
5.4.2 加算レイヤの実装
加算レイヤの実装では目新しいものはありません。逆伝搬時には逆伝搬の入力をそのまま出力にコピーしています。
(define-class add-layer (layer))
(defun make-add-layer (input-dimensions)
(make-instance 'add-layer
:input-dimensions input-dimensions
:output-dimensions input-dimensions
:forward-out (make-mat input-dimensions)
:backward-out (list (make-mat input-dimensions) ; dx
(make-mat input-dimensions)))) ; dy
(defmethod forward ((layer add-layer) &rest inputs)
(let ((out (forward-out layer)))
(copy! (car inputs) out)
(axpy! 1.0 (cadr inputs) out)))
(defmethod backward ((layer add-layer) dout)
(bind ((out (backward-out layer))
((dx dy) out))
(copy! dout dx)
(copy! dout dy)
out))
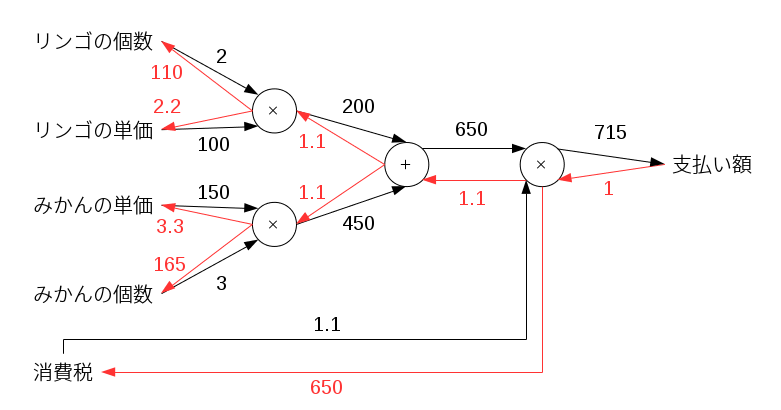
さて、次の図は本文中の図5-17に相当するものです。乗算レイヤと加算レイヤとを組み合わせてリンゴとみかんを買うときの支払い額の計算と、その逆伝搬を表しています。赤い矢印が出力に対する微分を表しています。例えば、リンゴの個数に入ってくる赤矢印は「リンゴの個数に対する支払い額の変化率」を表すので、リンゴの個数が1個増えれば支払い額は110円増えるということになります。
これに対応するプログラムを書くと以下のようになります。まず入力を設定し、forwardを繰り返して支払い額を計算します。それからbackwardを繰り返して各入力に対する支払い額の変化率を出力しています。
;; inputs
(defparameter n-apple (make-mat '(1 1) :initial-element 2.0))
(defparameter apple (make-mat '(1 1) :initial-element 100.0))
(defparameter orange (make-mat '(1 1) :initial-element 150.0))
(defparameter n-orange (make-mat '(1 1) :initial-element 3.0))
(defparameter tax (make-mat '(1 1) :initial-element 1.1))
;; layers
(defparameter mul-apple-layer (make-multiple-layer '(1 1)))
(defparameter mul-orange-layer (make-multiple-layer '(1 1)))
(defparameter add-apple-orange-layer (make-add-layer '(1 1)))
(defparameter mul-tax-layer (make-multiple-layer '(1 1)))
;; forward
(let* ((apple-price (forward mul-apple-layer apple n-apple))
(orange-price (forward mul-orange-layer orange n-orange))
(all-price (forward add-apple-orange-layer apple-price orange-price))
(price (forward mul-tax-layer all-price tax)))
(print price))
;; #<MAT 1x1 AB #2A((715.0))>
;; backward
(bind ((dprice (make-mat '(1 1) :initial-element 1.0))
((dall-price dtax) (backward mul-tax-layer dprice))
((dapple-price dorange-price) (backward add-apple-orange-layer dall-price))
((dorange dnorange) (backward mul-orange-layer dorange-price))
((dapple dnapple) (backward mul-apple-layer dapple-price)))
(print (list dnapple dapple dorange dnorange dtax)))
;; (#<MAT 1x1 AB #2A((110.0))> #<MAT 1x1 AB #2A((2.2))>
;; #<MAT 1x1 B #2A((3.3000002))> #<MAT 1x1 B #2A((165.0))>
;; #<MAT 1x1 AB #2A((650.0))>)
5.5 活性化関数レイヤの実装
5.5.1 ReLUレイヤ
ReLUは
- 順伝搬時: 入力値が正ならそれ自身、ゼロ以下なら0を返す
- 逆伝搬時: 順伝搬時の入力値が正なら逆伝搬の入力をそのまま通し、ゼロ以下なら0を返す
という関数です。つまり順伝搬時の入力値が正かどうかをマスク行列として保存しておく必要があります。
(define-class relu-layer (layer)
zero
mask)
(defun make-relu-layer (input-dimensions)
(make-instance 'relu-layer
:input-dimensions input-dimensions
:output-dimensions input-dimensions
:forward-out (make-mat input-dimensions)
:backward-out (make-mat input-dimensions)
:zero (make-mat input-dimensions :initial-element 0.0)
:mask (make-mat input-dimensions :initial-element 0.0)))
(defmethod forward ((layer relu-layer) &rest inputs)
(let ((zero (zero layer))
(mask (mask layer))
(out (forward-out layer)))
;; set mask
(copy! (car inputs) mask)
(.<! zero mask)
;; set output
(copy! (car inputs) out)
(.max! 0.0 out)))
(defmethod backward ((layer relu-layer) dout)
(geem! 1.0 dout (mask layer) 0.0 (backward-out layer)))
(.<! zero mask)はzeroとmaskの要素ごとの比較を行ない、maskの方が大きければ1を、そうでなければ0をmaskの位置の行列に代入します。(.max! 0.0 out)はスカラーと行列を引数に取り、行列の各要素とスカラー(この場合0)の比較を行ない、大きい方をoutの位置の行列に代入します。
これにより順伝搬の入力値が正なら1、ゼロ以下なら0となるような行列maskができています。逆伝搬時にはこのmaskとdoutとの要素積を取ればいいだけです。
5.5.2 Sigmoidレイヤ
Sigmoidレイヤの順伝搬では前回出てきた.logistic!関数を使います。sigmoid-layerクラスの定義では追加スロットはありませんが、逆伝搬時にforward-outに保存されている順伝搬の結果を使います。
(define-class sigmoid-layer (layer))
(defun make-sigmoid-layer (input-dimensions)
(make-instance 'sigmoid-layer
:input-dimensions input-dimensions
:output-dimensions input-dimensions
:forward-out (make-mat input-dimensions)
:backward-out (make-mat input-dimensions)))
(defmethod forward ((layer sigmoid-layer) &rest inputs)
(let ((out (forward-out layer)))
(copy! (car inputs) out)
(.logistic! out)))
(defmethod backward ((layer sigmoid-layer) dout)
(let ((y (forward-out layer))
(out (backward-out layer)))
(copy! y out)
(.+! -1.0 out) ; (-1 + y)
(geem! -1.0 y out 0.0 out) ; -y * (-1 + y)
(.*! dout out))) ; dout * -y * (-1 + y)
(.+! -1.0 out)は行列outの各要素にスカラー-1.0を足してoutを更新します。
(.*! dout out)は行列doutと行列outの要素積でoutを更新します。
行列からスカラーを引く関数がないので、 y * (y - 1) を計算するのに -y * (-1 + y) を計算しているのが若干トリッキーに見えるかもしれません。
5.6 Affine/Softmaxレイヤの実装
5.6.2 バッチ版Affineレイヤ
次に、入力を重み行列で線形変換してバイアスを足す、つまりアフィン変換を行うレイヤを定義します。ここまでは基本的に要素ごとの計算だったので行列の形はあまり意識してきませんでしたが、ここでは重要になってきます。
まずMGL-MATで行列はRow-major orderで作られており、行方向のデータがメモリ上で連続しています。そのため、1つのデータを行列の1行に対応させると後々扱いが便利になります。つまり、入出力の行列の行数はバッチサイズとなります。
(define-class affine-layer (layer)
x weight bias)
;; x: (batch-size, in-size)
;; y: (batch-size, out-size)
;; W: (in-size, out-size)
;; b: (out-size)
(defun make-affine-layer (input-dimensions output-dimensions)
(let ((weight-dimensions (list (cadr input-dimensions) (cadr output-dimensions)))
(bias-dimension (cadr output-dimensions)))
(make-instance 'affine-layer
:input-dimensions input-dimensions
:output-dimensions output-dimensions
:forward-out (make-mat output-dimensions)
:backward-out (list (make-mat input-dimensions) ; dx
(make-mat weight-dimensions) ; dW
(make-mat bias-dimension)) ; db
:x (make-mat input-dimensions)
:weight (make-mat weight-dimensions)
:bias (make-mat bias-dimension))))
(defmethod forward ((layer affine-layer) &rest inputs)
(let* ((x (car inputs))
(W (weight layer))
(b (bias layer))
(out (forward-out layer)))
(copy! x (x layer))
(fill! 1.0 out)
(scale-columns! b out)
(gemm! 1.0 x W 1.0 out)))
forwardでは、まずバイアスのベクトルbを列方向に伸長します。(fill! 1.0 out)でoutの中身を1.0で埋めて、(scale-columns! b out)でbの内容をoutの各行に掛けます。するとbの内容を列方向に積み上げたものがoutに入ります。Numpyのブロードキャストのようなものと考えてください。
最後に、gemm!一つでWに前からxを掛け、バイアスが入ったoutを足してout自身を更新しています。式で書くとこうなります。
out = 1.0 * x * W + 1.0 * out
前回はxは縦ベクトルとしていましたが、今回のxは横ベクトルをバッチサイズ分積み上げたものなので、Wの前から掛けています。
(defmethod backward ((layer affine-layer) dout)
(bind (((dx dW db) (backward-out layer)))
(gemm! 1.0 dout (weight layer) 0.0 dx :transpose-b? t) ; dx
(gemm! 1.0 (x layer) dout 0.0 dW :transpose-a? t) ; dW
(sum! dout db :axis 0) ; db
(backward-out layer)))
backwardの定義は本文中の図5-27の式
\frac{\partial L}{\partial X} = \frac{\partial L}{\partial Y} \cdot W^{\mathrm{T}}
\frac{\partial L}{\partial W} = X^{\mathrm{T}} \cdot \frac{\partial L}{\partial Y}
を素直に書き下したものになります。gemm!関数はキーワード引数として:transpose-a?と:transpose-b?を持っており、2つの行列のどちらでも、転置してから行列積を取ることができます。
バイアスの微分dbは、sum!関数を使ってdoutの行方向の和を取ることで、出力次元数のベクトルになります。
5.6.3 Softmax-with-lossレイヤ
softmax!関数の実装
次に3.5.2節の内容に従って、オーバーフロー対策版のソフトマックス関数を定義します。
\frac{\exp(a_k + C')}{\sum_{i=1}^n \exp(a_i + C')}
本文中ではC'としてaの最大の要素を使っていましたが、ここではaの平均値で引きます。
(defun average! (a batch-size-tmp)
(sum! a batch-size-tmp :axis 1)
(scal! (/ 1.0 (mat-dimension a 1)) batch-size-tmp))
(defun softmax! (a result batch-size-tmp &key (avoid-overflow-p t))
;; In order to avoid overflow, subtract average value for each column.
(when avoid-overflow-p
(average! a batch-size-tmp)
(fill! 1.0 result)
(scale-rows! batch-size-tmp result)
(axpy! -1.0 result a)) ; a - average(a)
(.exp! a)
(sum! a batch-size-tmp :axis 1)
(fill! 1.0 result)
(scale-rows! batch-size-tmp result)
(.inv! result)
(.*! a result))
これによってaの各要素についてソフトマックス関数を適用したものがresultに設定されます。ここでaも破壊的に変更されていることに注意が必要です。
cross-entropy!関数の実装
次に4.2.3節の内容に従って、ミニバッチ版のクロスエントロピー関数を定義します。
E=-\frac{1}{N}\sum_n\sum_k t_{nk} \log y_{nk}
(defun cross-entropy! (y target tmp batch-size-tmp &key (delta 1e-7))
(let ((batch-size (mat-dimension target 0)))
(copy! y tmp)
(.+! delta tmp)
(.log! tmp)
(.*! target tmp)
(sum! tmp batch-size-tmp :axis 1)
(/ (asum batch-size-tmp) batch-size)))
ここでlogがオーバーフローを起こさないようにlogの引数に微小な値deltaを足しています。
また、asumは行列の要素を全部足したスカラーを返す関数です。
softmax/loss-layerの実装
ここまでに定義したsoftmax!とcross-entropy!関数を使ってsoftmax/loss-layerのforwardを定義できます。このレイヤのforwardは入力xとone-hot表現で表されているtargetの2引数を取ります。
(define-class softmax/loss-layer (layer)
loss y target batch-size-tmp)
(defun make-softmax/loss-layer (input-dimensions)
(make-instance 'softmax/loss-layer
:input-dimensions input-dimensions
:output-dimensions 1
:backward-out (make-mat input-dimensions)
:y (make-mat input-dimensions)
:target (make-mat input-dimensions)
:batch-size-tmp (make-mat (car input-dimensions))))
(defmethod forward ((layer softmax/loss-layer) &rest inputs)
(bind (((x target) inputs)
(tmp (target layer)) ; layerのtargetスロットを一時領域として使う
(y (y layer))
(batch-size-tmp (batch-size-tmp layer)))
(copy! x tmp)
(softmax! tmp y batch-size-tmp) ; 入力にソフトマックス関数を適用してyに設定
(let ((out (cross-entropy! y target tmp batch-size-tmp))) ; yとtargetからクロスエントロピーを計算
(copy! target (target layer))
(setf (forward-out layer) out)
out)))
(defmethod backward ((layer softmax/loss-layer) dout)
(let* ((target (target layer))
(y (y layer))
(out (backward-out layer))
(batch-size (mat-dimension target 0)))
(copy! y out)
(axpy! -1.0 target out)
(scal! (/ 1.0 batch-size) out)))
5.7 誤差逆伝搬法の実装
5.7.2 誤差逆伝播法に対応したニューラルネットワークの実装
さて、必要なレイヤを定義してきましたので、いよいよニューラルネットのクラスを定義していきます。とりあえず構造は固定して2層のニューラルネットとし、活性化関数はReLUとします。
(define-class network ()
layers last-layer batch-size)
(defun make-network (input-size hidden-size output-size batch-size
&key (weight-init-std 0.01))
(let* ((network
(make-instance
'network
:layers (vector
(make-affine-layer (list batch-size input-size)
(list batch-size hidden-size))
(make-relu-layer (list batch-size hidden-size))
(make-affine-layer (list batch-size hidden-size )
(list batch-size output-size)))
:last-layer (make-softmax/loss-layer (list batch-size output-size))
:batch-size batch-size))
(W1 (weight (svref (layers network) 0)))
(W2 (weight (svref (layers network) 2))))
;; 重み行列を正規分布で初期化
(gaussian-random! W1)
(scal! weight-init-std W1)
(gaussian-random! W2)
(scal! weight-init-std W2)
network))
ニューラルネットはレイヤのベクタを持ち、affine-layerの重み行列はとりあえず正規分布で初期化しています。
次にニューラルネットの順伝搬を実行し、予測を出すためにpredict関数を定義します。予測を出すだけなら出力を正規化する必要はないので、最終層を除いたレイヤで先頭から順にforwardを実行していけばミニバッチに対する予測が出せます。
それに加えて最終層のforwardを実行し、クロスエントロピーの値を出力するnetwork-loss関数を定義します。
(defun predict (network x)
(loop for layer across (layers network) do
(setf x (forward layer x)))
x)
(defun network-loss (network x target)
(let ((y (predict network x)))
(forward (last-layer network) y target)))
network-loss関数を実行すると、ネットワーク全体に対する順伝搬の計算と設定が終わります。
勾配を計算するためには、network-lossを実行した後に、最終層から逆順にbackwardを実行していきます。
(defun set-gradient! (network x target)
(let ((layers (layers network))
dout)
;; forward
(network-loss network x target)
;; backward
(setf dout (backward (last-layer network) 1.0))
(loop for i from (1- (length layers)) downto 0 do
(let ((layer (svref layers i)))
(setf dout (backward layer (if (listp dout) (car dout) dout)))))))
このset-gradient!関数を実行すると、逆伝搬の値がnetworkに設定されます。学習時にはこれを取り出して利用することになります。
データの読み込み
データセットは1行に1データが入るような、データ数×特徴次元数のMGL-MATの行列とします。
libsvm形式のテキストファイルからこのような行列を作る関数を書いてみます。
(defmacro do-index-value-list ((index value list) &body body)
(let ((iter (gensym))
(inner-list (gensym)))
`(labels ((,iter (,inner-list)
(when ,inner-list
(let ((,index (car ,inner-list))
(,value (cadr ,inner-list)))
,@body)
(,iter (cddr ,inner-list)))))
(,iter ,list))))
(defun read-data (data-path data-dimension n-class &key (most-min-class 1))
(let* ((data-list (svmformat:parse-file data-path))
(len (length data-list))
(target (make-array (list len n-class)
:element-type 'single-float
:initial-element 0.0))
(datamatrix (make-array (list len data-dimension)
:element-type 'single-float
:initial-element 0.0)))
(loop for i fixnum from 0
for datum in data-list
do (setf (aref target i (- (car datum) most-min-class)) 1.0)
(do-index-value-list (j v (cdr datum))
(setf (aref datamatrix i (- j most-min-class)) v)))
(values (array-to-mat datamatrix) (array-to-mat target))))
MGL-MATの行列にmrefでアクセスするのはとても遅いので、いったんCommon Lispの二次元配列に値を設定し、それをarray-to-matでMGL-MATの行列に一気に変換する方が速いです。
MNISTデータを読み込む
それでは実際にlibsvm形式のMNISTのデータをダウンロードして読み込んでみます。
特徴次元数は784、クラス数は10、クラス番号は0からスタートになっているので、次のようにread-data関数を呼び出し、結果を変数に設定しおきます。
(multiple-value-bind (datamat target)
(read-data "/home/wiz/datasets/mnist.scale" 784 10 :most-min-class 0)
(defparameter mnist-dataset datamat)
(defparameter mnist-target target))
(multiple-value-bind (datamat target)
(read-data "/home/wiz/datasets/mnist.scale.t" 784 10 :most-min-class 0)
(defparameter mnist-dataset-test datamat)
(defparameter mnist-target-test target))
(setf *print-mat* nil)
mnist-dataset ; => #<MAT 60000x784 BF {100D316113}>
実際に評価してみると60000×784の行列であることが分かります。
データの一部を切り取ってミニバッチに設定する
このデータセットから一部分をミニバッチとして切り出すset-mini-batch!を定義します。とはいえ、元のデータセットには何も変更を加えず、参照領域を変えているだけです。
元のデータセットの形に戻すための関数reset-shape!も定義しておきます。
このようにすれば、実際のデータの移動をともなわないので、とても高速にミニバッチを設定できます。
(defun set-mini-batch! (dataset start-row-index batch-size)
(let ((dim (mat-dimension dataset 1)))
(reshape-and-displace! dataset
(list batch-size dim)
(* start-row-index dim))))
(defun reset-shape! (dataset)
(let* ((dim (mat-dimension dataset 1))
(len (/ (mat-max-size dataset) dim)))
(reshape-and-displace! dataset (list len dim) 0)))
;; 先頭から100個のデータのみを参照する
(set-mini-batch! mnist-dataset 0 100) ; => #<MAT 0+100x784+46961600 BF {100D316113}>
;; 以降は100×784のデータとして扱える
mnist-dataset ; => #<MAT 0+100x784+46961600 BF {100D316113}>
;; 元に戻す
(reset-shape! mnist-dataset)
;; #<MAT 60000x784 BF {100D316113}>
訓練の実行
1つのミニバッチ対して勾配を計算し、確率的勾配降下法でパラメータを更新する関数trainを書いてみます。
(defun train (network x target &key (learning-rate 0.1))
(set-gradient! network x target)
(bind ((layer (aref (layers network) 0))
((dx dW dB) (backward-out layer)))
(declare (ignore dx))
(axpy! (- learning-rate) dW (weight layer))
(axpy! (- learning-rate) dB (bias layer)))
(bind ((layer (aref (layers network) 2))
((dx dW dB) (backward-out layer)))
(declare (ignore dx))
(axpy! (- learning-rate) dW (weight layer))
(axpy! (- learning-rate) dB (bias layer))))
実際の学習では、まずニューラルネットのオブジェクトを生成し、それからデータセットの中からランダムに起点を選んでミニバッチを設定します。本文中では個々のデータをランダムに選んでいたのですが、それはめんどくさそうだったので妥協しました。
ミニバッチの設定が終わったらtrain関数を実行します。これを十分な数繰り返せば学習が進行していくはずです。
(defparameter mnist-network (make-network 784 50 10 100))
(time
(loop repeat 10000 do
(let* ((batch-size (batch-size mnist-network))
(rand (random (- 60000 batch-size))))
(set-mini-batch! mnist-dataset rand batch-size)
(set-mini-batch! mnist-target rand batch-size)
(train mnist-network mnist-dataset mnist-target))))
予測とテスト
前述したpredict関数はバッチサイズ×クラス数の行列を出力します。実際の予測結果であるクラス番号を出すためには、行ごとの最大値を出す必要があります。「行列の軸ごとに最大値となるようなインデックスを返す」ようなAPIが見当らなかったので自分で書いてみました。計測してみたところ、Numpyのargmaxと同程度の速さにはなりました。
(defun max-position-column (arr)
(declare (optimize (speed 3) (space 0) (safety 0) (debug 0))
(type (array single-float) arr))
(let ((max-arr (make-array (array-dimension arr 0)
:element-type 'single-float
:initial-element most-negative-single-float))
(pos-arr (make-array (array-dimension arr 0)
:element-type 'fixnum
:initial-element 0)))
(loop for i fixnum from 0 below (array-dimension arr 0) do
(loop for j fixnum from 0 below (array-dimension arr 1) do
(when (> (aref arr i j) (aref max-arr i))
(setf (aref max-arr i) (aref arr i j)
(aref pos-arr i) j))))
pos-arr))
(defun predict-class (network x)
(max-position-column (mat-to-array (predict network x))))
(predict-class mnist-network mnist-dataset)
;; #(5 0 4 1 9 2 1 3 1 4 3 5 3 6 1 7 2 8 6 9 4 0 9 1 1 2 4 3 2 7 3 8 6 9 0 5 6 0 7
;; 6 1 8 7 9 3 9 8 5 9 3 3 0 7 4 9 8 0 9 4 1 4 4 6 0 4 5 6 1 0 0 1 7 1 6 3 0 2 1
;; 1 7 0 0 2 6 7 8 3 9 0 4 6 7 4 6 8 0 7 8 3 1)
次に、データセット全体に対して予測モデルの正答率を出す関数accuracyを定義します。
(defun accuracy (network dataset target)
(let* ((batch-size (batch-size network))
(dim (mat-dimension dataset 1))
(len (/ (mat-max-size dataset) dim))
(cnt 0))
(loop for n from 0 to (- len batch-size) by batch-size do
(set-mini-batch! dataset n batch-size)
(set-mini-batch! target n batch-size)
(incf cnt
(loop for pred across (predict-class network dataset)
for tgt across (max-position-column (mat-to-array target))
count (= pred tgt))))
(* (/ cnt len) 1.0)))
訓練とテストを繰り返すプロセス
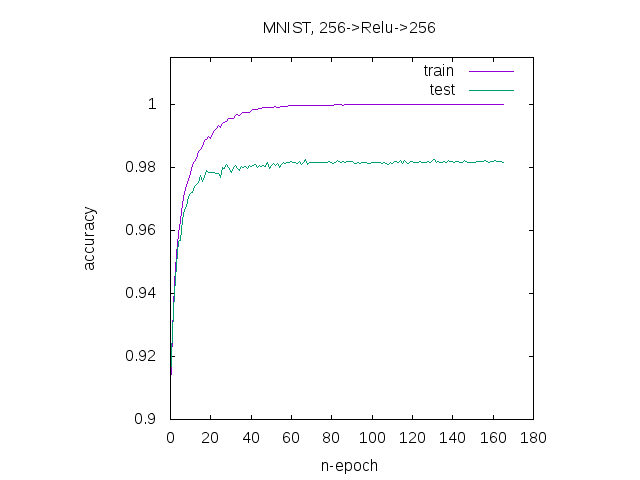
こうしてミニバッチに対する訓練とテストを行う関数ができたので、それらを組み合わせて実際の学習プロセス全体を書きます。途中、600サイクルごとに訓練データセットとテストデータセットに対するaccuracyの値を出力します。(データセットのサイズが60000で、バッチサイズが100なのでつまり1エポックごと)
途中経過はtrain-acc-listとtest-acc-listにプッシュしていきます。
(defparameter mnist-network (make-network 784 256 10 100))
(defparameter train-acc-list nil)
(defparameter test-acc-list nil)
(loop for i from 1 to 100000 do
(let* ((batch-size (batch-size mnist-network))
(rand (random (- 60000 batch-size))))
(set-mini-batch! mnist-dataset rand batch-size)
(set-mini-batch! mnist-target rand batch-size)
(train mnist-network mnist-dataset mnist-target)
(when (zerop (mod i 600))
(let ((train-acc (accuracy mnist-network mnist-dataset mnist-target))
(test-acc (accuracy mnist-network mnist-dataset-test mnist-target-test)))
(format t "cycle: ~A~,15Ttrain-acc: ~A~,10Ttest-acc: ~A~%" i train-acc test-acc)
(push train-acc train-acc-list)
(push test-acc test-acc-list)))))
cycle: 600 train-acc: 0.9099333 test-acc: 0.9152
cycle: 1200 train-acc: 0.929 test-acc: 0.9298
cycle: 1800 train-acc: 0.94366664 test-acc: 0.9435
cycle: 2400 train-acc: 0.9512333 test-acc: 0.9494
cycle: 3000 train-acc: 0.9597 test-acc: 0.9557
cycle: 3600 train-acc: 0.96281666 test-acc: 0.9594
cycle: 4200 train-acc: 0.9680167 test-acc: 0.9642
cycle: 4800 train-acc: 0.97211665 test-acc: 0.9683
cycle: 5400 train-acc: 0.97398335 test-acc: 0.9697
cycle: 6000 train-acc: 0.97715 test-acc: 0.9712
以下略
結果のプロット
グラフをプロットするには自作のライブラリclgplotを使います。これはGnuplotのフロントエンドで、シーケンスやシーケンスのシーケンスからグラフをプロットしたりできます。
これはQuicklispに登録されていないので、Roswellなどを使ってGithubのレポジトリからインストールします。
ros install masatoi/clgplot
Lisp処理系に移り、quickloadでclgplotを読み込みます。実際のプロットではplots関数にシーケンスのシーケンスを渡します。
(ql:quickload :clgplot)
(clgp:plots (list (reverse train-acc-list)
(reverse test-acc-list))
:main "MNIST, 256->Relu->256"
:title-list '("train" "test")
:x-label "n-epoch"
:y-label "accuracy"
:y-range '(0.9 1.015))
学習できているようです。
ベンチマーク
『ゼロから作る Deep Learning』のリポジトリにPythonのコードがあったので、hidden-sizeを色々変えながら訓練部分にかかる時間を計測してみました。
なお環境は
- Ubuntu 16.04 LTS
- CPU: Core i5 6440
- GPU: Geforce GTX 750 Ti
- CUDA: 8.0
- OpenBLAS: 0.2.18-1ubuntu1 (aptで入るやつ)
| hidden-size | SBCL1.4.3 + MGL-MAT(OpenBLAS) | SBCL1.4.3 + MGL-MAT(cuBLAS) | Python3.6 + Numpy(OpenBLAS) |
|---|---|---|---|
| 50 | 6.252 sec | 4.882 sec | 11.773 sec |
| 256 | 13.12 sec | 6.709 sec | 42.274 sec |
| 512 | 27.18 sec | 8.552 sec | 73.334 sec |
自分の環境ではNumpyでもMGL-MATのCPUモードでもOpenBLASを使うように設定しているので、同じバックエンドにも関わらずこれだけの速度差が出るのは驚きでした。
次回
各種オプティマイザの実装、各種初期化法の実装、Batch Normalization