最適化パッケージCVXRがCRANに登場したので、そのご紹介をします。
CVXR: An R Package for Disciplined Convex Optimization
このパッケージは凸最適化問題を解くために開発されたMATLAB CVXライブラリのR版といった位置づけのものです。
同様のプロジェクトとしてPythonのCVXPYやJuliaのConvex.jlといったプロジェクトがある。
実際の使用感はCVXPYのR版クローンという印象です。
このCVXRを使うことで、凹凸が分かる数式の組み合わせにで表現された問題を効率よく解く事が出来ます。
実際に解くソルバーにはECOSやSCSを選んで使用することが可能です。
より詳しい内容は Stanfordの説明サイト を参照すると良いです。
実際の使い方
基本的には次の5ステップで使うことになります。
- 変数の宣言
- 制約条件を設定する
- 目的関数を定義する
- ソルバーで解く
- 実行結果を確認し、必要な情報を取り出す
目的関数
目的関数はMaximizeやMinimizeを設定することができます。
制約条件を満たす変数の組が得られれば良いという場合は
objective <- Minimize(0)
のように問題を定義してやればOKです。
変数
最適化を行う変数はBool、Int、Variable等で定義が可能でBoolは真偽値、Intは整数、Variableは実数として扱われます。
整数計画問題はNP困難な問題なので、特別な理由がない限り変数にIntを使うのは避けるべきです。
制約条件
制約条件は変数について普通に使うRの関数と等式/不等式を用いて記述しlistで束ねて持つことになります。
制約はスカラとしても、ベクターとしても定義することができます。
なので、1番目の要素だけ制約をかけるとか、全体のsumをとるとどうなる、といった書き方のどちらも可能です。
実際に使える関数はCVXR Functionsにある関数が制約条件の記述のために使うことができます。
Solve
最適化問題を解くには、シンプルに solve()をするだけでOKです。
解いた結果をresultというオブジェクトに保存したとすると、
最適化結果は$status
目的関数の値は$value
解いた時のメタ情報は$solver, $solve_time, $num_itersといったスロットにそれぞれ保存されています。
変数がそれぞれどんな値になったか?が見たい場合もあると思います。
その場合は```result$getValue()``というスロットがつくられるので
getValue()に宣言してある変数を渡せば結果が得られます。
具体例
例えば、5人で食事をして72000を割り勘したいんだけど1人が2万円出してくれるんで
残りの人で上手く割り勘したい、という簡単な問題であれば次のように表現して解くことができる。
x <- Variable(10, name="x") # 変数の宣言
constraints <- list() # 目的変数の定義
constraints <- c(constraints, x > 0) # 非負制約
constraints <- c(constraints, sum(x) == 72000) # 合計金額
constraints <- c(constraints, x[1] == 20000) # ふとっぱら!!
obj1 <- Minimize(0) # 問題関数の定義
o1 <- Problem(obj1, constraints) # 問題と制約条件をまとめて。。。
result <- solve(o1) # Solverで問題を解く
print(result$status)
print(result$value) # 目的関数の値を確認 ここでは目的関数は0の定数なので0が得られるはず
print(result$getValue(x))
実際に実行すると次のように、制約条件通りに解けているのが確認できます。
[1,] 20000.000
[2,] 5777.778
[3,] 5777.778
[4,] 5777.778
[5,] 5777.778
[6,] 5777.778
[7,] 5777.778
[8,] 5777.778
[9,] 5777.778
[10,] 5777.778
ここでは実数として解いているので、小数値となっています。
同様の方法でナップザック問題やネットワークフロー最適化、ポートフォリオ最適化といった
OR系の問題を記述し解く事ができます。
他にも公式にあるチュートリアルから1題そのまま写経ですが。。。
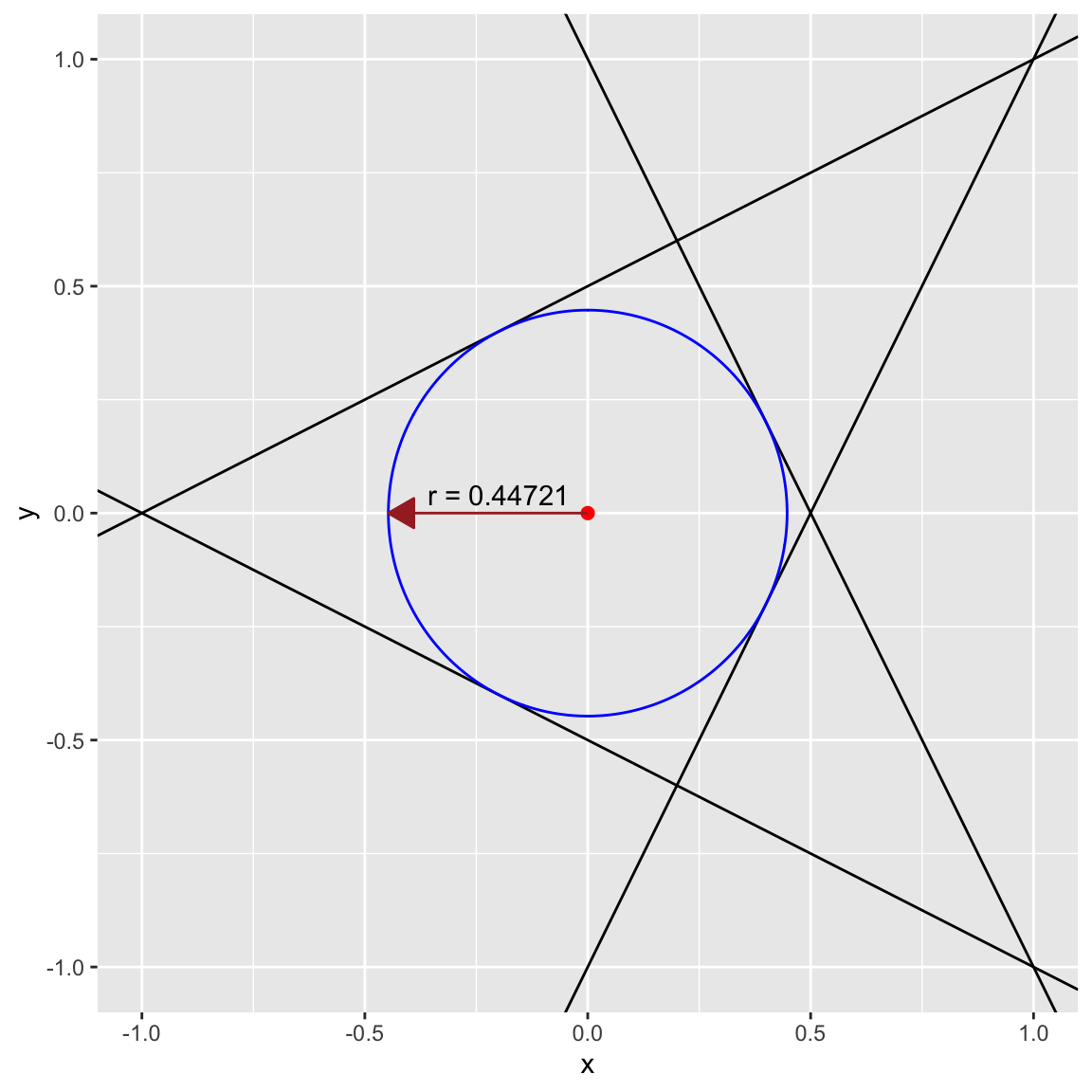
直線に囲まれた領域に縁を描いたときに、その円の半径は最大でどれくらいになるか?という問題も次のよう解けます。
a1 <- matrix(c(2,1))
a2 <- matrix(c(2,-1))
a3 <- matrix(c(-1,2))
a4 <- matrix(c(-1,-2))
b <- rep(1,4)
r <- Variable(name = "radius")
x_c <- Variable(2, name = "center")
obj <- Maximize(r)
constraints <- list(
t(a1) %*% x_c + p_norm(a1, 2) * r <= b[1],
t(a2) %*% x_c + p_norm(a2, 2) * r <= b[2],
t(a3) %*% x_c + p_norm(a3, 2) * r <= b[3],
t(a4) %*% x_c + p_norm(a4, 2) * r <= b[4]
)
p <- Problem(obj, constraints)
result <- solve(p)
radius <- result$getValue(r)
center <- result$getValue(x_c)
library(ggplot2)
library(ggforce)
ggplot() +
geom_abline(slope = -a1[1] / a1[2], intercept = b[1] / a1[2]) +
geom_abline(slope = -a2[1] / a2[2], intercept = b[2] / a2[2]) +
geom_abline(slope = -a3[1] / a3[2], intercept = b[3] / a3[2]) +
geom_abline(slope = -a4[1] / a4[2], intercept = b[4] / a4[2]) +
geom_circle(mapping = aes(x0 = center[1], y0 = center[2], r = radius), color = "blue") +
geom_point(mapping = aes(x = center[1], y = center[2]), color = "red", size = 2) +
geom_line(mapping = aes(x = c(center[1], center[1] - radius), y = c(center[2], center[2])),
arrow = arrow(length = unit(0.03, "npc"), ends = "first", type = "closed"),
color = "brown") +
annotate("text", x = -0.2, y = 0.04, label = sprintf("r = %0.5f", radius)) +
labs(x = "x", y = "y") +
xlim(-1, 1) + ylim(-1, 1)
2017年時点ではBoolの扱いが未だでとりあえずVariableになってるっぽい等、
未実装分があるみたいですが、今後整備されるのを期待しましょう!! ENJOY!