1. サーモグラフィの色表現
温度センサなどで計測した気温をサーバに送り可視化する場合、サーモグラフィのように温度の高低を色で表現したいときがあります。
また、サーモグラフィの表現は温度に限らず、数値の大小を色で表現する場合に有効です。
直感的には任意の値を青色→緑色→赤色と並んだ色相に割り当て3色の値を取得するだけでいいのですが、
プログラムで表現しようとするとやりたいことに対して少し面倒です。
変換したい値の範囲を0.0〜1.0の範囲かつRGB各色が0~255の値をとるとすると、サーモグラフィ風の色表現はおおよそ以下のような色変化を行います。
| 変換したい値 | R | G | B | RGBで表現される色 |
|---|---|---|---|---|
| 0.0 | 0 | 0 | 255 | 青 |
| 0.25 | 0 | 200 | 200 | 水色 |
| 0.5 | 0 | 255 | 0 | 緑 |
| 0.75 | 200 | 200 | 0 | 橙 |
| 1.0 | 255 | 0 | 0 | 赤 |
この色変化プログラムで再現する方法としてif文で細かく条件分けして記述する手法がとられている場合が多いようです。しかし、何らかの関数で近似することでよりきめ細かい色変化を再現できるのではと考えました。
すでに投稿されている内容としては下記の記事があります。こちらの記事では各所の色が変化する部分をCOS関数で近似させています。しかしこの場合も0に張り付いている部分や1に張り付いている部分は場合分けが必要になります。
- 各色の色の変化は以下のような区間分けができます。
- 0に張り付いている区間
- 連続的に滑らかに値が変化する区間
- 1に張り付いている区間
このような変化を行う関数としてシグモイド関数を適用させることにしました。
3. シグモイド関数
シグモイド関数は生物の神経細胞が持つ性質をモデルとして作られた関数です。ある値を境に急激に変化を行うため、ニューラルネットワークの活性化関数に用いられています。
式は以下の通りです。
αはゲインとなり、この値を変えることで、変化の勾配を変えることができます。
sigmoid(x) = \frac{\tanh(αx/2)+1}{2}
-1 <= x <= 1
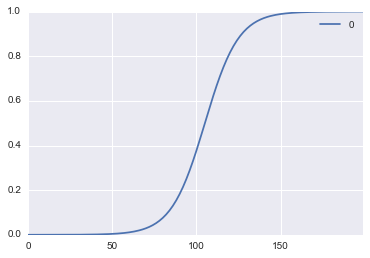
また、上記の式は以下のグラフになります。
4. 色相環へのシグモイド関数の適用
赤色はシグモイド関数をそのまま利用します。青色は関数を反転させたものを利用します。緑については赤色と青色の関数を加算して実現しています。詳細は下記のコードを参照してください。
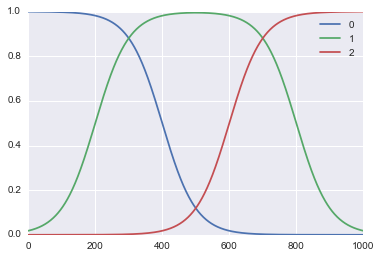
Pythonで実装すると以下のようになります。Jupyterで実行すると上掲のグラフを確認することができます。
ゲインとオフセットの値を変更することで、値のグラデーションの重なり具合を変更することができます。
sigmoidメソッドは上記のシグモイド関数の式をそのまま実装しました。colorBarRGBメソッドで上記で説明した各色の関数を作成しています。結果は各色0.0〜1.0で出力されるので、16bitの場合は各色1024をかけた結果が実際の値になります。
import numpy as np
from pandas import DataFrame as df
import matplotlib.pyplot as plt
%matplotlib inline
gain = 10
offset_x= 0.2
offset_green = 0.6
def sigmoid(x, gain=1, offset_x=0):
return ((np.tanh(((x+offset_x)*gain)/2)+1)/2)
def colorBarRGB(x):
x = (x * 2) - 1
red = sigmoid(x, gain, -1*offset_x)
blue = 1-sigmoid(x, gain, offset_x)
green = sigmoid(x, gain, offset_green) + (1-sigmoid(x,gain,-1*offset_green))
green = green - 1.0
return (blue,green,red)
# 入力値は0.0〜1.0の範囲
data = [colorBarRGB(x*0.001) for x in range(0,1000)]
color = df(data)
color.plot()
上記の結果を8bit(0〜255)の画像に変換した結果が以下になります。

上記方法ですとかなり短いコードでサーモグラフィの表現を実現することができると思います。また、ゲインとオフセットを調整することで、グラデーションの重なり具合を変更し細かい調整がやりやすそうです。