観測データを増やしていくことで確率を更新していくベイズ統計学の基本的な考え方です。
例えば、赤球と白球が入った袋Aと袋Bがあったとします。
袋Aには(赤球,白球)=(6,4)
袋Bには(赤球,白球)=(5,5)
の分だけそれぞれの球が入っていることがわかっているとします。
ここで、A,Bどちらの袋であるかがわかっていない状態で袋から玉を取り出してみてA,Bどちらかを言い当てるということをしてみましょう。
(※ただし取り出した球は色を見た後すぐに復路に戻すとします。)
一回目: 赤が出ました。さて、どちらの袋でしょうか? …当然一回しか取り出していないのでわかりませんね(笑)
二回目: 赤が出ました。また赤です。もう一回取り出してみます。
三回目: 赤が出ました。なんとなくこの袋は赤が多いようだからAっぽいな。。。?
と回数を重ねていき、赤が出た回数が多ければ多いほど袋Aである確率(確信)が頭の中で更新されていくイメージが湧くかと思います。
これがいわゆるベイズ更新と言われるものです。データが多ければ多いほど精度は良くなっていくという直感的に理解しやすいのではないでしょうか?
今回はこのベイズ更新をpythonを使って実装していきます。
import matplotlib.pyplot as plt #グラフを描画するためのモジュール
import pandas as pd #統計分析用のモジュール
import numpy as np #多次元配列における計算をするためのモジュール 統計データは多次元配列であるこ
とが多いためよく使われる
from scipy.stats import bernoulli #確率分布を利用したい場合に用いるモジュール 今回の場
合、確率分布はAかBか、表か裏かという、二択の場合によく用いられるベルヌーイ分布を用いる。
plt.style.use('ggplot')
#パラメータの設定
p_A = 4.0/10.0 #Aの球を選んできた場合に赤の玉を選んでくる確率
p_B = 5.0/10.0 #Bの球を選んできた場合に赤の玉を選んでくる確率
p_prior = 0.5 #どちらを選んだのか、よくわからないからとりあえずA,Bの二択であることからAを選んだ確
率を0.5と設定しておく
#0を白、1を赤球とする
data = [0,0,1,0,1,0] #所得データ
num_data = 2 #使用するデータの個数 データの個数を増やすほどに、事後確率の精度が上がっていく
likelihood_A = bernoulli.pmf(data[:num_data], p_A) #袋Aに関してベルヌーイ分布に従う
球の選び方の確率密度関数(尤度関数)を出力 num_data番目までのデータを使用 p_Aの部分は、1の時の確
率を渡す
likelihood_B = bernoulli.pmf(data[:num_data], p_B) #袋Bに関してベルヌーイ分布に従う
球の選び方の確率密度関数(尤度関数)を出力 num_data番目までのデータを使用 p_Bの部分は、1の時の確
率を渡す
p_A_posterior = p_prior #Aの事後分布(更新前)
p_B_posterior = p_prior #Bの事後分布(更新前)
p_A_posterior *= np.prod(likelihood_A)
p_B_posterior *= np.prod(likelihood_B)
#正規化(足したら1になるように調整する)
normal = p_A_posterior + p_B_posterior
p_A_posterior /= normal
p_B_posterior /= normal
df = pd.DataFrame([p_A_posterior,p_B_posterior],columns=["post"])
x = np.arange(df.shape[0])
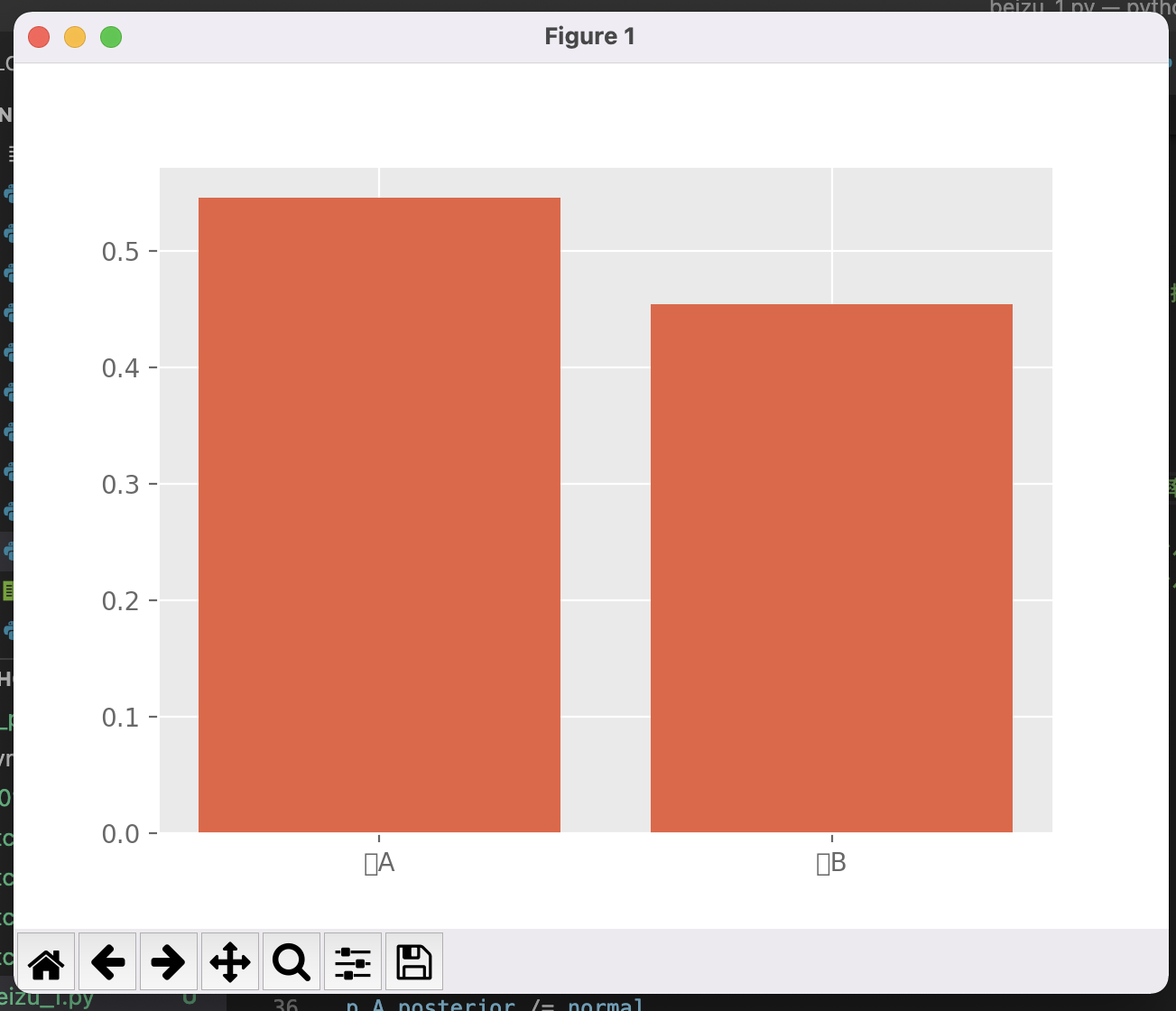
plt.bar(x,df["post"])
plt.xticks(x,["袋A","袋B"]) #メモリに名前をつけたい場合に用いる
plt.show() #描画
#取り出す回数が1回だけの場合(使用するデータが1回目だけ、つまり、num_data = 1)の出力結果
一回だけだと、どっちなのかよくわからない状況ですが....
回数を増やしていくごとに確率の精度が上がっていくのが実感できると思うのでぜひ試してみてください。