Elixirで並列レイトレーサーを作った話 その1

今回、初投稿になります。

【2020/03/20：注釈】 ここでは defstruct を多用していますが、なるべくリストやマップなどの組み込みデータ構造を使ったほうが良いです。

普段は自然言語処理の会社でC++中心にコードを書いているのですが、趣味ではElixirを書いてます。今回は会社のセミナーでも話したレイトレーシングをElixirで書いた話です。長いので2回に分けます。今回はElixirでのレイトレーサーの解説を、次回は並列化とベンチマークを中心に書こうと思います。

また、今回の記事は

RAY TRACEING IN ONE WEEKENDを元にしています。Amazonでも$３くらいで買えますし、公式サイトで無料でダウンロードできるので興味があればそちらもどうぞ。

この記事の対象

• Elixirに興味のある人
• プログラミングElixirを読み終えて、ちょっと違うことをやってみたい人
• Elixirの並列処理に興味がある人
• ElixirをWeb以外でも使ってみたい人

基本的にElixirの並列化のパフォーマンスあたりがメインになってますので、今回はそのベンチマークに使ったレイトレーサーの話で、並列化は出てきません。Elixirの基礎を勉強してる人にはちょっとわかりにくいかも知れませんがElixirがわからなくても、他言語の経験が豊富なら理解できる内容だと思います。

レイトレーサーとはなにか

レイトレーシングは3DCGレンダリングの手法の一つでカメラの位置から光線(レイ)を描画するビューポートの各ピクセルに向かって飛ばして、最初に当たった、つまり最も近い物体の色を描画する、という単純な手法です。ピクセルごとに疎なので、並列化してもプロセスごとの干渉は起こりません。

画像の出力

まずは結果を表示する必要があるので、画像を出力します。
画像の出力はerlportを使ってpythonのPillowのImageを使います。
連携に関しては
Elixir＋Keras＝手軽に高速な「データサイエンスプラットフォーム」 ～Flowでのマルチコア活用事例～なんかが参考になると思います。

簡単に書きます

ライブラリを利用する

mix.exs

  defp deps do
    [
      {:erlport, "~> 0.10.0" }, 
    ]

と依存性を記載して、

$ mix deps.get

でライブラリがインストールされます。

Pythonのコード

続いて呼び出されるpython側実装ですが

image.py

from PIL import Image
import numpy as np

def show(arr):
  img_arr = np.array(arr)
  img = Image.fromarray(np.uint8(img_arr))
  img.show()

引数の配列をnumpyのarray化して画像出力するだけです。

Elixirからerlportを通してpythonを呼ぶ

では、Elixirから呼んでみます。

raytracer_ex.ex

 def show(arr) do
    { :ok, py_exec } = :python.start( [ python_path: 'lib' ] )
    :python.call( py_exec, :image, :show, [arr] )
    :python.stop( py_exec )
  end

python_path: 'lib'でlib直下にpythonのファイルがあることをerlportに伝えて、:python.callに取得したパス指定のpy_execとimage.pyを示す :imageと関数名:show、そして引数をリストで渡します。arrは行数×列数×3(RGB)の3次元配列です。

では、これを使って、グラデーションを出力してみます。

raytracer_ex.ex

  def gradation() do
    nx = 200
    ny = 100
    for y <- ny-1..0 do
      for x <- 0..nx-1 do
        [x / nx, y / ny, 0.2]
        |> Enum.map(&(255 * &1))
      end
    end
  end
  |> show

左下を黒にするためにループは逆にしています。
結果は

となります。

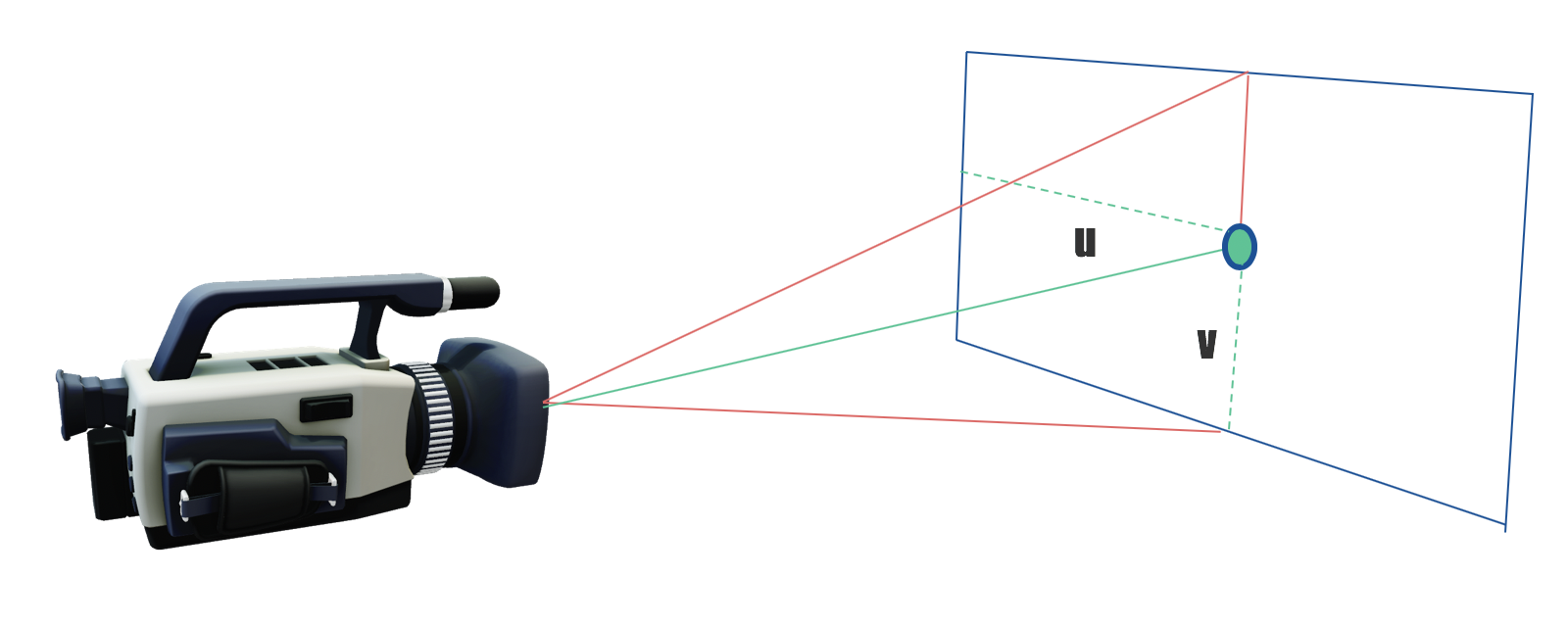
光線を定義する

光線

光線はカメラから各ピクセルに向かって発せられます。
ここで知りたい情報は、物体とどれくらいの距離で当たったか、です。
そのため、定義する必要があるのは、光線の始点の位置ベクトルと方向ベクトルです。ベクトルと言っていますが、位置ベクトルは(0, 0, 0)の点を基準にどれくらい離れているか、なので、通常の位置と考えて問題ありません。

一方、方向ベクトルは向きと大きさだけを持っているもので、それにtをかけた位置でぶつかる物体の近さをtの大きさ比較します。要は定規として使われるものです。tがマイナスだと始点より後ろの描画範囲外になるので、基本的にtは整数になります。

Vec3を定義

まず、光線の定義に必要な(x, y, z)を持つモジュールを定義します。

lib/raytracer_ex/vector.ex

defmodule RaytracerEx.Vector do
  defmodule Vec3 do
    defstruct x: 0.0, y: 0.0, z: 0.0
    alias RaytracerEx.Vector.Vec3, as: Vec3
    def vec3(list) when is_list(list) do
      [x | rest] = list
      [y | [z]] = rest
      %Vec3{x: x, y: y, z: z}
    end
    def ones() do
      %Vec3{x: 1.0, y: 1.0, z: 1.0}
    end
    def add(vec1, vec2) do
      %Vec3{x: vec1.x + vec2.x, y: vec1.y + vec2.y, z: vec1.z + vec2.z }
    end
    def dot(vec1, vec2) do
      vec1.x * vec2.x + vec1.y * vec2.y + vec1.z * vec2.z
    end
    def mult(vec1, vec2) do
      %Vec3{x: vec1.x * vec2.x, y: vec1.y * vec2.y, z: vec1.z * vec2.z }
    end
    def scale(vec, s) do
      %Vec3{x: vec.x * s, y: vec.y * s, z: vec.z * s }
    end
    def sub(vec1, vec2) when is_map vec2 do
      %Vec3{x: vec1.x - vec2.x, y: vec1.y - vec2.y, z: vec1.z - vec2.z }
    end
    def sub(vec, s) do
      %Vec3{x: vec.x - s, y: vec.y - s, z: vec.z - s}
    end
    def len(vec) do
      :math.sqrt(lengthSqr(vec))
    end
    def lengthSqr(vec) do
      vec.x * vec.x + vec.y * vec.y + vec.z * vec.z
    end
    def div(vec, scalar) do
      %Vec3{x: vec.x / scalar, y: vec.y / scalar, z: vec.z / scalar}
    end
    def unit_vector(vec) do
      s = len(vec)
      Vec3.div(vec, s)
    end
    def cross(vec1, vec2) do
      x = vec1.y * vec2.z - vec1.z * vec2.y
      y = vec1.z * vec2.x - vec1.x * vec2.z
      z = vec1.x * vec2.y - vec1.y * vec2.x
      %Vec3{x: x, y: y, z: z}
    end
    def to_list(vec3) do
      [vec3.x, vec3.y, vec3.z]
    end
  end
end

光線を実装

簡潔です。

lib/raytracer_ex/ray.ex

defmodule RaytracerEx.Ray do
  alias RaytracerEx.Vector.Vec3, as: Vec3
  defstruct pos: %Vec3{}, dir: %Vec3{}

  def at(vec, t), do: Vec3.add(vec.pos, (Vec3.scale(vec.dir, t)))
end

光線を使って空を描画する

光線を単位ベクトル化して、y成分を元に空(背景)を描画してみます。

raytracer_ex.ex

  def sky() do
    nx = 200
    ny = 100
    low_left = Vec3.vec3([-2.0, -1.0, -1.0])
    horizontal = Vec3.vec3([4.0, 0.0, 0.0])
    vertical = Vec3.vec3([0.0, 2.0, 0.0])
    origin = Vec3.vec3([0.0, 0.0, 0.0])
    for y <- ny-1..0 do
      for x <- 0..nx-1 do
        u = x / nx
        v = y / ny
        ray = %Ray{pos: origin, 
                   dir: Vec3.scale(horizontal, u) 
                        |> Vec3.add(Vec3.scale(vertical, v)) 
                        |> Vec3.add(low_left)
              }
        unit_vec = Vec3.unit_vector(ray.dir)
        t = 0.5 * (unit_vec.y + 1.0)
        color = Vec3.scale(Vec3.ones(), (1.0 - t))
                |> Vec3.add(Vec3.scale(Vec3.vec3([0.5, 0.7, 1.0]), t))
        [color.x, color.y, color.z] |> Enum.map(&(&1 * 255))
      end
    end
    |> show
  end

単位ベクトルというのはx, y, zを足して1になるベクトルです。長さで割って算出するので、

sqrt(x^2 + y^2 + z^2)

として中心を0とすると、最小で-1になります。1足して0.5で割ると0〜１の範囲になります。1-tで白を、tが青の割合として計算しています。足して1ということはx,z成分があるとy成分は小さくなるので、(x, 0, z)が最小で、横や上にいくにつれて青くなるもので、結果は

となります。

Elixirのfor文について

あまり言及がないのですが、レイトレーサーを書いてて気づいたのは、Elixirのfor文は配列を加工、もしくは生成するものみたいです。個人的にElixirを使ってて思うのはデータをリストの形にして、mapやreduceで加工するような処理に最適化されている、ということです。
for文の解釈も結構面白くて、2重ループだと2次元配列、変数の宣言をまとめて書くと2変数でも1次元配列になったりします。

単体の球の追加

では、次に球をシーンに追加してみましょう。
CGは一種の完璧な物体で簡単な計算だけで描画が可能です。CGを扱ってる人間は皆球が大好きです。多分。

球を描くのに、当たり判定をする必要があります。
まず、球の公式ですが、半径rで球上の座標(x, y, z)に対し

x^2 + y^2 + z^2 = r^2

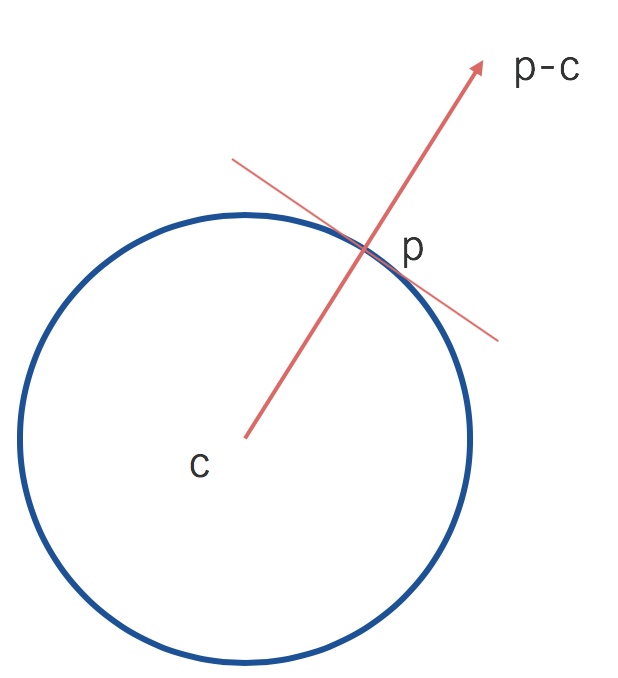
が成立します。これを位置ベクターで書いてみます。球の中心をc、球上の点をpとします。

\vec{c} = (cx, cy, cz), \vec{p} = (x, y, z) \\
(x - cx)^2 + (y - cy)^2 + (z - cz)^2 = r^2 \\
= (\vec{p} - \vec{c}) ・(\vec{p} - \vec{c}) = r^2

当たり判定を考える時、レイトレーシングではレイを使います。レイと球の交点は

p(t) = \vec{o} + t\vec{d}

になります。これは球の表面の1点ということになり、上記公式に当てはめると

(p(t) - \vec{c}) ・(p(t) - \vec{c}) = r^2

交点を右辺に変換して

(\vec{o}+t\vec{d} - \vec{c}) ・(\vec{o}+t\vec{d} - \vec{c}) = r^2

ここで、後のコードでも使っていますが、

oc = \vec{o} - \vec{c}

と置いて展開すると

（\vec{d}・\vec{d})t^2 + 2(\vec{d}・oc)t + (oc・oc)-r^2=0

これはtについての2次方程式とみなすことができ、2次方程式(通常xを使うところを光線用にtにしています)

at^2 + bt + c = 0

の解の公式

t = \frac{-b\pm\sqrt{b^2-4ac}}{2a}

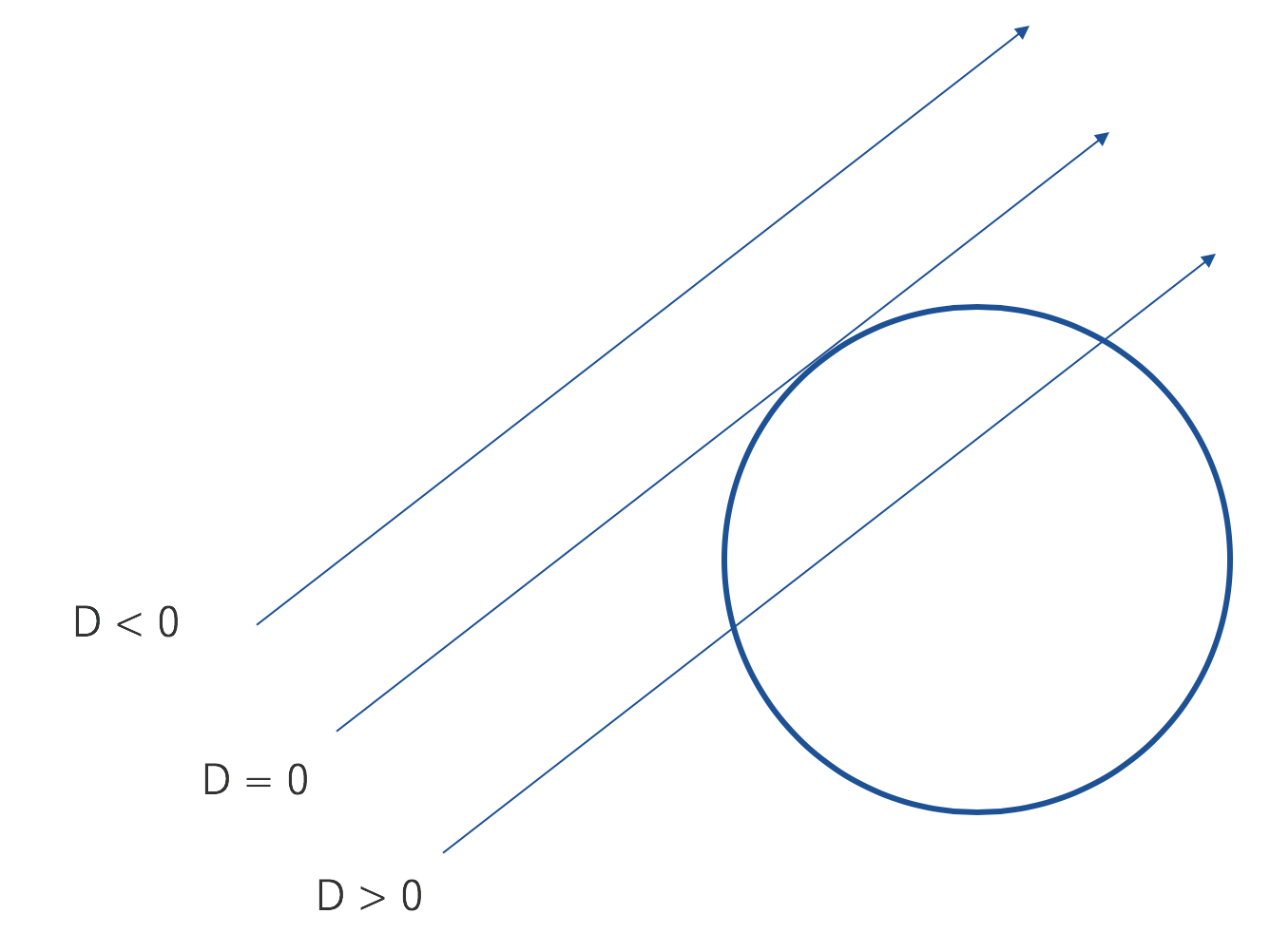
これに関しては複数の球の際に、最前面の球を判定する際に使いますが、単体の球であれば、当たったかどうか、だけで十分です。ここで判別式を使います。

D = b^2 - 4ac

このDが0より小さいと接点はなく、0の場合、表面の点で接する、つまり接線、0より大きければ、球を貫通する、2点の表面と触れるということになります。

これをコードに落とすと

raytracer_ex.ex

  def hit_sphere(center, radius, ray) do
    oc = Vec3.sub(ray.pos, center)
    a = Vec3.dot(ray.dir, ray.dir)
    b = Vec3.dot(oc, ray.dir) * 2.0
    c = Vec3.dot(oc, oc) - radius * radius
    discriminant = b * b - 4 * a * c
    discriminant > 0.0
  end

さらにこれを使って球を描きます。当たった部分を赤く描いてみます。

raytracer_ex.ex

  def sphere_color(ray) do
    if hit_sphere(Vec3.vec3([0.0, 0.0, -1.0]), 0.5, ray) do
      Vec3.vec3([1.0, 0.0, 0.0])
    else
      unit_vec = Vec3.unit_vector(ray.dir)
      t = 0.5 * (unit_vec.y + 1.0)
      Vec3.scale(Vec3.ones(), (1.0 - t))
          |> Vec3.add(Vec3.scale(Vec3.vec3([0.5, 0.7, 1.0]), t))
    end
  end
  def draw_sphere() do
    nx = 200
    ny = 100
    low_left = Vec3.vec3([-2.0, -1.0, -1.0])
    horizontal = Vec3.vec3([4.0, 0.0, 0.0])
    vertical = Vec3.vec3([0.0, 2.0, 0.0])
    origin = Vec3.vec3([0.0, 0.0, 0.0])
    for y <- ny-1..0 do
      for x <- 0..nx-1 do
        u = x / nx
        v = y / ny
        ray = %Ray{pos: origin, 
                   dir: Vec3.scale(horizontal, u) 
                        |> Vec3.add(Vec3.scale(vertical, v)) 
                        |> Vec3.add(low_left)
              }
        color = sphere_color(ray)
        [color.x, color.y, color.z] |> Enum.map(&(&1 * 255))
      end
    end
    |> show
  end

結果は

複数の球を描く

一つでは味気ないので増やしてみます。

衝突情報モジュールの作成

まずは、複数の球に光線が当たった場合の衝突情報を保持するモジュールを作ります。

lib/raytracer_ex/hitrec.ex

defmodule RaytracerEx.HitRec do
  defstruct t: 0.0, pos: %Vec3{}, normal: %Vec3{}
end

normalは法線のことです。それについては少し先で説明します。

衝突判定を物体モジュールに持つ

球以外物体にも対応できるように物体モジュールの中に移動します。本来、hitableモジュール内に球を定義して、hitableモジュールのhitでそれぞれのhitを呼ぶ作りが良い気がします。

lib/raytracer_ex/sphere.ex

defmodule RaytracerEx.Sphere do
  @name :sphere

  alias RaytracerEx.Vector.Vec3, as: Vec3
  alias RaytracerEx.HitRec, as: HitRec
  alias RaytracerEx.Ray, as: Ray

  defstruct type: @name, r: 0.0, center: %Vec3{}

  def hit(sphere, ray, t_min, t_max) do
    oc = Vec3.sub(ray.pos, sphere.center)
    a = Vec3.dot(ray.dir, ray.dir)
    b = Vec3.dot(oc, ray.dir)
    c = Vec3.dot(oc, oc) - sphere.r * sphere.r
    disc = b * b - a * c
    if disc > 0.0 do
      root = :math.sqrt(disc)
      t = (-b - root) / a
      if t_min < t and t < t_max do
        pos = Ray.at(ray, t)
        {true, %HitRec{t: t, pos: pos, 
                       normal: Vec3.sub(pos, sphere.center) |> Vec3.div(sphere.r)}}
      else
        t = (-b + root) / a
        if t_min < t and t < t_max do
          pos = Ray.at(ray, t)
          {true, %HitRec{t: t, pos: pos, 
                         normal: Vec3.sub(pos, sphere.center) |> Vec3.div(sphere.r)}}
        else
          {false, nil}
        end            
      end
    else
      {false, nil}
    end
  end
end

ifが多くてちょっとかっこ悪いですね。
ここで、ルートの近い方を先に判定するように、また、2を消しても平気なので取り除いてます。ここでの戻り値は当たったかのフラグと衝突情報のタプルです。

複数の物体での当たり判定

複数の物体に対して判定を行います。

raytracer_ex.ex

  defp _hit(objects, ray, t_min, t_max) do
    objects
    |> Enum.map(fn obj ->
      case obj.type do
        :sphere -> Sphere.hit(obj, ray, t_min, t_max)
      end
    end)
    |> Enum.filter(&(elem(&1, 0)))
    |> Enum.sort(&(elem(&1, 1).t < elem(&2, 1).t))
    |> Enum.take(1)
    |> Enum.map(&(elem(&1, 1)))
  end

発表ではEnum.map で判定を行いましたが、事後処理が多くなったのでEnum.reduceで書き換えています。結果が一番いいもので更新していく場合、Enum.reduceが一番向いています。メモリ効率もこの方が良いです。

描画します。

raytracer_ex.ex

  def draw_spheres() do
    nx = 200
    ny = 100
    low_left = Vec3.vec3([-2.0, -1.0, -1.0])
    horizontal = Vec3.vec3([4.0, 0.0, 0.0])
    vertical = Vec3.vec3([0.0, 2.0, 0.0])
    origin = Vec3.vec3([0.0, 0.0, 0.0])
    objects = [%Sphere{center: Vec3.vec3([0.0, 0.0, -1.0]), r: 0.5},
               %Sphere{center: Vec3.vec3([0.0, -100.5, -1.0]), r: 100.0}]
    for y <- ny-1..0 do
      for x <- 0..nx-1 do
        color = 
        u = x / nx
        v = y / ny
        ray = %Ray{pos: origin, 
                   dir: Vec3.scale(horizontal, u) 
                      |> Vec3.add(Vec3.scale(vertical, v)) 
                      |> Vec3.add(low_left)
              }
        obj_arr = _hit(objects, ray, 0.001, 999999)
        color =
        if obj_arr == [] do
          Vec3.add((hd obj_arr).normal, Vec3.ones()) |> Vec3.scale(0.5)
        else
          _sky(ray)
        end
        [color.x, color.y, color.z]|> Enum.map(&(&1 * 255)) 
      end
    end
    |> show
  end

2番目の大きい球の上に小さい球が乗っているシーンで、色は法線を元に描いています。

アンチエイリアス

ちょっと球の重なりがギザギザしているので、ここでアンチエイリアスをかけます。
ジャギる原因としては、

• ピクセルは小さな四角なので、そのままはっきり色を付けると凸凹になる
• 色の境目がはっきりしすぎ

ということなので、色を周辺と混ぜるとなめらかになります。サンプル数を100として、ランダムに0〜１をx,yに足したものでu, vを算出することで、そのピクセルを中心にいくつかのサンプルで周辺の色を取得して足し合わせて、最後にサンプル数で割ることで平滑化を行います。

raytracer_ex.ex

  def antialias() do
    nx = 200
    ny = 100
    ns = 100
    low_left = Vec3.vec3([-2.0, -1.0, -1.0])
    horizontal = Vec3.vec3([4.0, 0.0, 0.0])
    vertical = Vec3.vec3([0.0, 2.0, 0.0])
    origin = Vec3.vec3([0.0, 0.0, 0.0])
    objects = [%Sphere{center: Vec3.vec3([0.0, 0.0, -1.0]), r: 0.5},
               %Sphere{center: Vec3.vec3([0.0, -100.5, -1.0]), r: 100.0}]
    for y <- ny-1..0 do
      for x <- 0..nx-1 do
        color = 
        for s <- 1..ns do
          u = (x + :rand.uniform()) / nx
          v = (y + :rand.uniform()) / ny
          ray = %Ray{pos: origin, 
                  dir: Vec3.scale(horizontal, u) 
                        |> Vec3.add(Vec3.scale(vertical, v)) 
                        |> Vec3.add(low_left)
              }
          _color(ray, objects)
        end
        |> Enum.reduce(%Vec3{}, fn c, color -> Vec3.add(color, c) end)
        |> Vec3.div(ns)
        [color.x, color.y, color.z]
        |> Enum.map(&(:math.sqrt(&1) * 255)) 
      end
    end
    |> show
  end

:rand.uniform()は等確率で0〜1の間の少数を生成します。xで言うと、x座標+0〜1/200なので、極小なずれになり、ほとんどがピクセルの色になります。

法線と拡散反射

法線

何度か出てきている法線、英語ではnormalで変数名でも使っています。法線は、面を極小に縮めた際に限りなく直線に近づいたその直線から垂直方向の線で、反射はこの法線を元に計算されます。球の法線は非常に簡単で表面の点から中心を引いた、つまり、中心から表面の点に向けて突き抜けた方向が法線の方向になります。

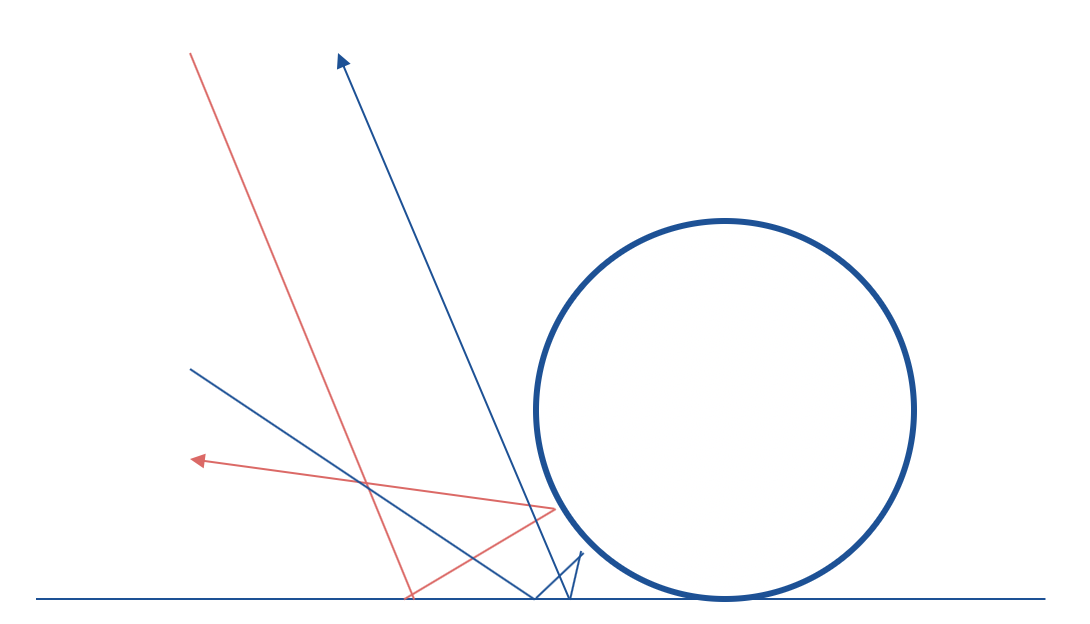
拡散反射

法線で光線が反射する、と言っても実際の物体の表面はミクロレベルで見ると小さな凸凹があります。それで法線がずれて乱反射することを拡散反射といいます。

raytracer_ex.ex

  defp _random_in_unit_shpere() do
    p = Vec3.vec3([:rand.uniform(), :rand.uniform(), :rand.uniform()])
        |> Vec3.scale(2.0)
        |> Vec3.sub(Vec3.ones())
    if Vec3.lengthSqr(p) < 1.0, do: p, else: _random_in_unit_shpere()
  end
  defp _color(ray, objects) do
    obj_arr = _hit(objects, ray, 0.001, 999999)
    if obj_arr != [] do 
      obj = hd obj_arr
      target = Vec3.add(obj.pos, obj.normal) |> Vec3.add(_random_in_unit_shpere())
      _color(%Ray{pos: obj.pos, dir: Vec3.sub(target, obj.pos)}, objects) |> Vec3.scale(0.5)
    else
      _sky(ray)
    end
  end

_random_in_unit_sphere()では0〜１の乱数を2倍して1引くことで-1〜１に変換し、それが、半径1の円に収まる範囲にして反射を調整しています。
アンチエイリアスの_colorを上記に変更すると

だいぶCGっぽくなりました。ここで、影の判定（ぶつかったところから光源の間に物体があるか）のようなことをしていないのに影ができているのは重なりのある部分は乱反射が多くなり、_colorでは跳ね返るたびに再帰した上で色を半減しているため、半分ずつ色が吸収されて暗くなるためです。ここでの再帰は最終的に空に抜けた部分で色が確定しますが、その際、跳ね返った回数だけ0.5をかけた係数でrgbが0に近づきます。

ガンマ補正

ここで色が暗いので、補正をかけます。
gamma 2を使う場合、sqrtでapproximationが可能です。
アンチエイリアスのサンプル数で割った後に255を掛ける前にsqrtを呼んであげると

いい感じになりました。

マテリアル（材質の追加）

拡散反射では空の色を反射率一律0.5で描画しましたが、実際の物体はもっと複雑です。表面の材質を定義することでより物体をリアルにします。

材質モジュールの追加

ここでは材質モジュールを定義して、その中にそれぞれの材質をサブモジュールとして追加します。それぞれに関数scatterを持たせて呼び元では大本のRaytracer.Material.scatter()で呼び出します。scatterの中身はそれぞれ説明していきます。
追加するモジュールは

• ランバート
• メタル
• 絶縁体（屈折）
  です。

lib/raytracer_ex/material.ex

defmodule RaytracerEx.Material do
  alias RaytracerEx.Vector.Vec3, as: Vec3
  defmodule Lambertian do
    @name :lambertian
    defstruct type: @name, albedo: %Vec3{}
    def scatter(lam, _ray, hitrec) do
    end
  end
  defmodule Metal do
    @name :metal
    defstruct type: @name, albedo: %Vec3{}, fuzz: 1.0
    def scatter(metal, ray, hitrec) do
    end
  end
  defmodule Dielectric do
    @name :dielectric
    defstruct type: @name, ri: 1.0
    def scatter(diel, ray, hitrec) do
    end
  end

  def scatter(material, ray, hitrec) do
    case material.type do
      :lambertian -> Lambertian.scatter(material, ray, hitrec)
      :metal      -> Metal.scatter(material, ray, hitrec)
      :dielectric -> Dielectric.scatter(material, ray, hitrec)
    end
  end
end

衝突情報に材質を追加

衝突時に材質も渡す必要があるので、構造体に追加します。

lib/raytracer_ex/hitrec.ex

defmodule RaytracerEx.HitRec do
  alias __MODULE__, as: HitRec
  alias RaytracerEx.Vector.Vec3, as: Vec3
  alias RaytracerEx.Material.Lambertian, as: Lambertian
  defstruct t: 0.0, pos: %Vec3{}, normal: %Vec3{}, material: %Lambertian{}

  def new(t, p, n, mat) do
    %HitRec{t: t, pos: p, normal: n, material: mat}
  end
end

構造体の要素が増えてきたので、ついでに簡略化したnew関数を作っています。
また、初期値はランバートにしています。

ランバート材質

ランバート、もしくはランベルトはそこらへんにある普通の材質です。反射率を表すalbedoを持ちます。反射率と言うと鏡面体を想像してしまいますが、実際のところ、物体は色を持っているわけではありません。光の色ごとに吸収するか反射するかがあって、反射する場合に色がついて見える、ということになります。なので、反射率で赤のみ1.0の場合に緑の光を当てると全て吸収して黒く見えたりします。

ランバートのscatter関数は

lib/raytracer_ex/material.ex

    def scatter(lam, _ray, hitrec) do
      target = Vec3.add(hitrec.pos, hitrec.normal) 
               |> Vec3.add(Ray.random_in_unit_sphere())

      {true, %Ray{pos: hitrec.pos, dir: Vec3.sub(target, hitrec.pos)}, lam.albedo}
    end

戻り値は散乱するかと跳ね返った光線と色（色の希薄化情報）です。
ランバートは固定の色を持つ材質なので必ずtrueを返します。

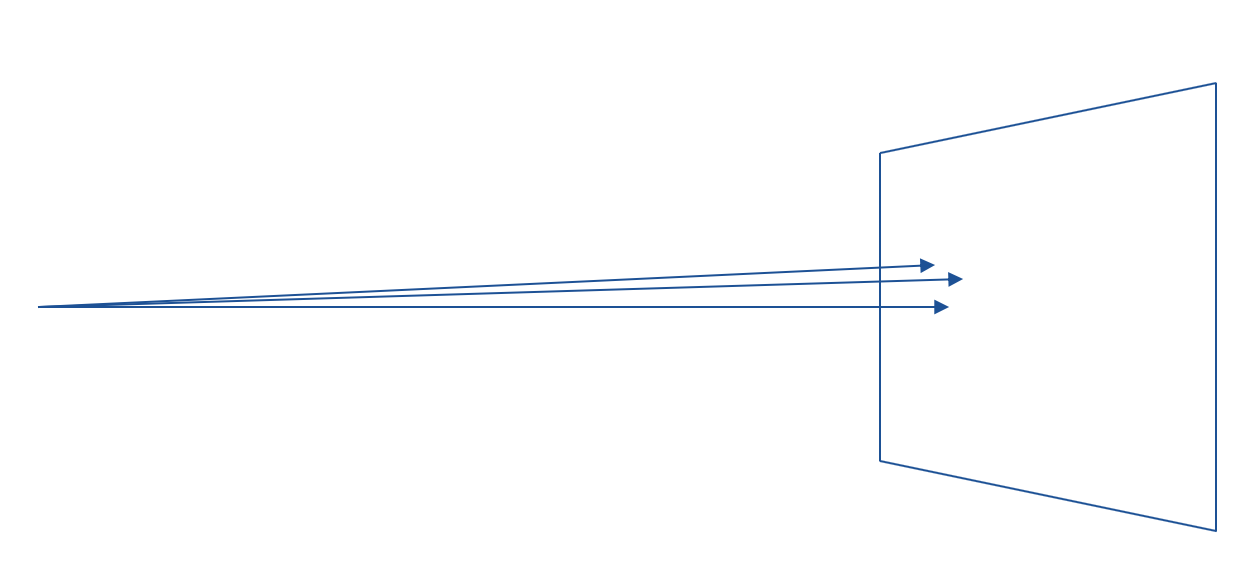
メタル（鏡面体）

メタルはalbedoとfuzｚを持ちます。また、反射を計算するのに、Utilsにreflect関数を作成しています。

lib/raytracer_ex/utils.ex

defmodule RaytracerEx.Utils do
  alias RaytracerEx.Vector.Vec3, as: Vec3
  def reflect(vec, normal) do
    Vec3.sub(vec, Vec3.scale(normal, Vec3.dot(vec, normal) * 2.0))
  end
end

反射は図のように衝突点からそのままベクトルを伸ばした点から、法線方向に衝突点までの2倍進めた方向へのベクトルで表されます。

\vec{r} = \vec{v} + 2 \vec{a}

で計算されます。これを使ってメタルのscatterは下記のようになります。

lib/raytracer_ex/material.ex

    def scatter(metal, ray, hitrec) do
      reflected = Utils.reflect(Vec3.unit_vector(ray.dir), hitrec.normal)
      scattered = %Ray{pos: hitrec.pos, 
                       dir: Vec3.add(reflected, Vec3.scale(Ray.random_in_unit_sphere(), metal.fuzz))}
      {(Vec3.dot(scattered.dir, hitrec.normal) > 0.0), scattered, metal.albedo}
    end

また、金属は100%反射するのでなく、鈍い反射がありうるので、fuzzをランダムな反射角にかけてブレを作っています。これが0だと全反射となります。また、反射方向と法線の内積がプラスになる場合のみ反射します。

まずはここまでで描画してみます。

raytracer_ex.ex

    sphere = %Sphere{center: %Vec3{x: 0.0, y: 0.0, z: -1.0}, r: 0.5, material: %Lambertian{albedo: Vec3.vec3([0.8, 0.3, 0.3])}}    
    sphere2 = %Sphere{center: %Vec3{x: 0.0, y: -100.5, z: -1.0}, r: 100, material: %Lambertian{albedo: Vec3.vec3([0.8, 0.8, 0.0])}}    
    sphere3 = %Sphere{center: %Vec3{x: 1.0, y: 0.0, z: -1.0}, r: 0.5, material: %Metal{albedo: Vec3.vec3([0.8, 0.6, 0.2]), fuzz: 1.0}}   
    sphere4 = %Sphere{center: %Vec3{x: -1.0, y: 0.0, z: -1.0}, r: 0.5, material: %Metal{albedo: Vec3.vec3([0.8, 0.8, 0.8]), fuzz: 0.3}}
    objects = [sphere, sphere2, sphere3, sphere4]

絶縁体（屈折）

英語でDielectricは絶縁体ですが、ここではガラスや水のような屈折する素材を指します。
ここでは屈折角を取得するrefract関数をUtilsに追加します。また、Dielectricは屈折の係数を構造体に持ちます。

lib/raytracer_ex/utils.ex

  def refract(vec, normal, ni_over_nt) do
    uv = Vec3.unit_vector(vec)
    dt = Vec3.dot(uv, normal)
    discriminant = 1.0 - ni_over_nt * ni_over_nt * (1.0 - dt * dt)
    if (discriminant > 0.0) do
      refracted = Vec3.sub(Vec3.scale(Vec3.sub(uv, Vec3.scale(normal, dt)), ni_over_nt), Vec3.scale(normal, :math.sqrt(discriminant)))
      {true, refracted}
    else
      {false, nil}
    end

lib/raytracer_ex/material.ex

    def scatter(diel, ray, hitrec) do
      reflected = Utils.reflect(ray.dir, hitrec.normal)
      attenuation = Vec3.ones()
      {outward_normal, ni_over_nt, cosine} = parse(diel, ray, hitrec)
      {is_refract, refracted} = Utils.refract(ray.dir, outward_normal, ni_over_nt)
      reflect_prob = if is_refract, do: schlick(cosine, diel.ri), else: 1.0
      scattered = if :rand.uniform() < reflect_prob, 
                     do: %Ray{pos: hitrec.pos, dir: reflected}, else: %Ray{pos: hitrec.pos, dir: refracted}
      {true, scattered, attenuation}
    end
    def parse(diel, ray, hitrec) do
      if Vec3.dot(ray.dir, hitrec.normal) > 0.0 do
       {Vec3.scale(hitrec.normal, -1.0), diel.ri, (Vec3.dot(ray.dir, hitrec.normal) * diel.ri) / (Vec3.len(ray.dir))}
      else
        {hitrec.normal, 1.0 / diel.ri, (Vec3.dot(ray.dir, hitrec.normal) * -1 * diel.ri) / (Vec3.len(ray.dir))}
      end
    end
    def schlick(cosine, ref_idx) do
      r0 = (1.0 - ref_idx) / (1.0 + ref_idx) |> :math.pow(2)
      r0 + (1.0 - r0) * :math.pow((1.0 - cosine), 5)
    end

ガラスはビー玉とかだと逆さまに風景が見えると思いますが、今回は2重に球を配置して、ガラスのように描画します。

raytracer_ex.ex

    sphere = %Sphere{center: %Vec3{x: 0.0, y: 0.0, z: -1.0}, r: 0.5, material: %Lambertian{albedo: Vec3.vec3([0.8, 0.3, 0.3])}}    
    sphere2 = %Sphere{center: %Vec3{x: 0.0, y: -100.5, z: -1.0}, r: 100, material: %Lambertian{albedo: Vec3.vec3([0.8, 0.8, 0.0])}}    
    sphere3 = %Sphere{center: %Vec3{x: 1.0, y: 0.0, z: -1.0}, r: 0.5, material: %Metal{albedo: Vec3.vec3([0.8, 0.6, 0.2])}}   
    sphere4 = %Sphere{center: %Vec3{x: -1.0, y: 0.0, z: -1.0}, r: 0.5, material: %Dielectric{ri: 1.5}}
    sphere5 = %Sphere{center: %Vec3{x: -1.0, y: 0.0, z: -1.0}, r: -0.45, material: %Dielectric{ri: 1.5}}

描画すると

カメラの設定

さて、球がいい感じになったところで、カメラを可変にしましょう。
ここでは工程2つ分まとめてすすめてしまいます。

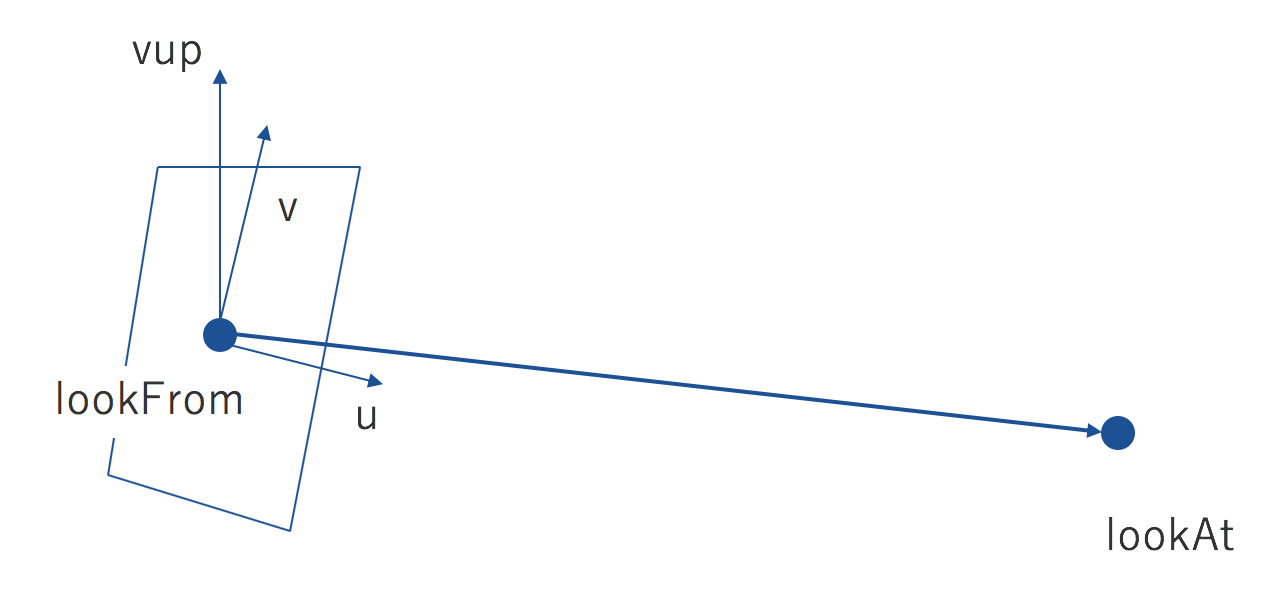
カメラは基本的にlookFromを始点として、lookAtに向けた角度、またvupを上方向を示すベクトルとして、カメラ起点のxyz座標、ここではuvwと置いた3次元座標を設定します。
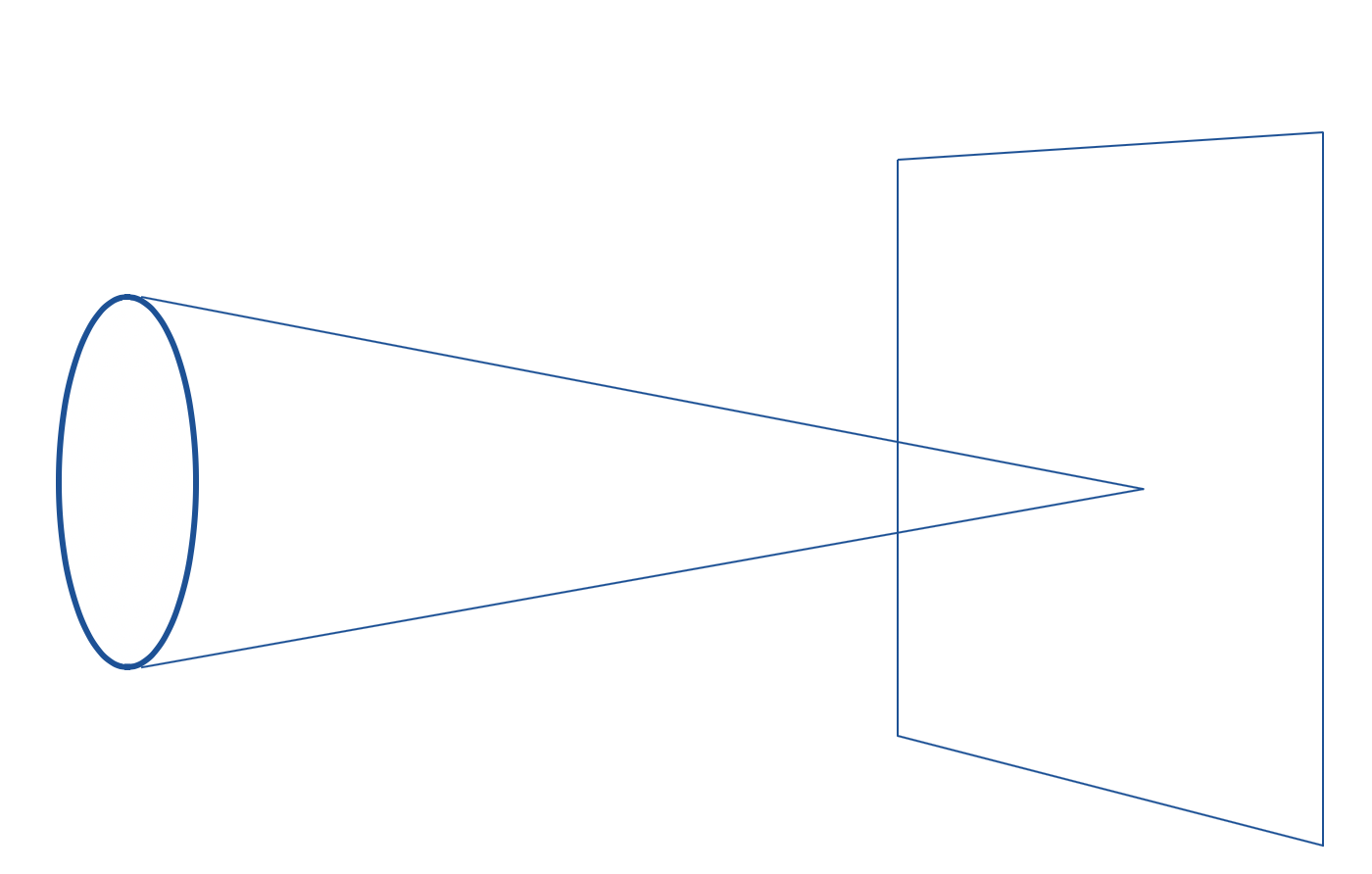
また、レンズを定義して、フォーカスのブレを作って奥行きを表現します。

lib/raytracer_ex/camera.ex

defmodule RaytracerEx.Camera do
  alias __MODULE__ , as: Camera
  alias RaytracerEx.Vector.Vec3, as: Vec3
  alias RaytracerEx.Utils, as: Utils
  alias RaytracerEx.Ray, as: Ray
  defstruct origin: %Vec3{}, low_left: %Vec3{}, horizontal: %Vec3{}, vertical: %Vec3{},
     u: %Vec3{}, v: %Vec3{}, w: %Vec3{}, lens_radius: 1.0

  def create(lookfrom, lookat, vup, vfov, aspect, aperture, focus_dist) do
    theta = vfov * :math.pi / 180
    half_height = :math.tan(theta * 0.5)
    half_width = aspect * half_height
    origin = lookfrom
    w = Vec3.sub(lookfrom, lookat) |> Vec3.unit_vector
    u = Vec3.cross(vup, w) |> Vec3.unit_vector
    v = Vec3.cross(w, u)
    lower_left = Vec3.sub(Vec3.sub(Vec3.sub(origin, Vec3.scale(u, focus_dist * half_width)), 
                                   Vec3.scale(v, focus_dist * half_height)),
                          Vec3.scale(w, focus_dist))
    horizontal = Vec3.scale(u, half_width * 2.0 * focus_dist)
    vertical = Vec3.scale(v, half_height * 2.0 * focus_dist)
    %Camera{origin: origin, horizontal: horizontal, 
            vertical: vertical, low_left: lower_left,
            u: u,  v: v, w: w, lens_radius: aperture * 0.5}
  end

  def get_ray(camera, s, t) do
    rd = Vec3.scale(random_in_unit_disk(), camera.lens_radius)
    offset = Vec3.add(Vec3.scale(camera.u, rd.x), Vec3.scale(camera.v, rd.y))
    dir = Vec3.add(camera.low_left, Vec3.scale(camera.horizontal, s))
          |> Vec3.add(Vec3.scale(camera.vertical, t))
          |> Vec3.sub(camera.origin)
          |> Vec3.sub(offset)

    %Ray{pos: Vec3.add(camera.origin, offset), dir: dir}
  end
  def random_in_unit_disk() do
    p = Vec3.sub(Vec3.vec3([:rand.uniform(), :rand.uniform(), 0.0]), 
                           Vec3.vec3([1.0, 1.0, 0.0]))
        |> Vec3.scale(2.0)
    if Vec3.dot(p, p) < 1.0, do: p, else: random_in_unit_disk()
  end
end

カメラの位置をずらして描画してみましょう。

raytracer_ex.ex

  def camera_test() do
    nx = 200
    ny = 100
    lookfrom = Vec3.vec3([-2.0, 2.0, 1.0])
    lookat = Vec3.vec3([0.0, 0.0, -1.0])
    dist_to_focus = Vec3.len(Vec3.sub(lookfrom, lookat))
    camera = Camera.create(lookfrom, lookat, Vec3.vec3([0.0, 1.0, 0.0]), 90.0, nx/ny, 0.0, dist_to_focus)

    sphere = %Sphere{center: %Vec3{x: 0.0, y: 0.0, z: -1.0}, r: 0.5, material: %Lambertian{albedo: Vec3.vec3([0.8, 0.3, 0.3])}}    
    sphere2 = %Sphere{center: %Vec3{x: 0.0, y: -100.5, z: -1.0}, r: 100, material: %Lambertian{albedo: Vec3.vec3([0.8, 0.8, 0.0])}}    
    sphere3 = %Sphere{center: %Vec3{x: 1.0, y: 0.0, z: -1.0}, r: 0.5, material: %Metal{albedo: Vec3.vec3([0.8, 0.6, 0.2])}}   
    sphere4 = %Sphere{center: %Vec3{x: -1.0, y: 0.0, z: -1.0}, r: 0.5, material: %Dielectric{ri: 1.5}}
    sphere5 = %Sphere{center: %Vec3{x: -1.0, y: 0.0, z: -1.0}, r: -0.45, material: %Dielectric{ri: 1.5}}
    scene = Scene.create_scene(nx, ny, camera, [sphere, sphere2, sphere3, sphere4, sphere5])

    Scene.render(scene)
  end

球を大量に描画する

準備は整ったので、球を大量に描画してみます。

raytracer_ex.ex

  def create_spheres() do
    nx = 200
    ny = 100
    lookfrom = Vec3.vec3([11.0, 2.0, 3.0])
    lookat = Vec3.vec3([0.0, 0.0, 0.0])
    dist_to_focus = Vec3.len(Vec3.sub(lookfrom, lookat))
    aperture = 0.1
    camera = Camera.create(lookfrom, lookat, Vec3.vec3([0.0, 1.0, 0.0]), 20.0, nx/ny, aperture, dist_to_focus)

    base = %Sphere{center: Vec3.vec3([0.0, -1000.0, 0.0]), r: 1000.0, material: %Lambertian{albedo: Vec3.vec3([0.5, 0.5, 0.5])}}
    ss= 
    for a <- -11..10, b <- -11..10 do
      choose_mat = :rand.uniform()
      center = Vec3.vec3([a + 0.9 * :rand.uniform(), 0.2, b + 0.9 * :rand.uniform()])
      if Vec3.len(Vec3.sub(center, Vec3.vec3([4.0, 0.2, 0.0]))) > 0.9 do
        if choose_mat < 0.8 do
          %Sphere{center: center, r: 0.2, 
                  material: %Lambertian{albedo: Vec3.vec3([:rand.uniform() * :rand.uniform(), :rand.uniform()*:rand.uniform(), :rand.uniform()*:rand.uniform()])}}
        else
          if choose_mat < 0.95 do
            %Sphere{center: center, r: 0.2,
                    material: %Metal{albedo: Vec3.vec3([0.5 * (1 + :rand.uniform()), 0.5 * (1 + :rand.uniform()), 0.5 * (1 + :rand.uniform())]), fuzz: 0.5 * :rand.uniform()}}
          else
            %Sphere{center: center, r: 0.2, material: %Dielectric{ri: 1.5}}
          end
        end
      end
    end
    |> Enum.filter(&(not is_nil(&1)))
    objects = [base]++ss
    objects = [%Sphere{center: Vec3.vec3([0.0, 1.0, 0.0]), r: 1.0, material: %Dielectric{ri: 1.5}}]++objects
    objects = [%Sphere{center: Vec3.vec3([-4.0, 1.0, 0.0]), r: 1.0, material: %Lambertian{albedo: Vec3.vec3([0.4, 0.2, 0.1])}}]++objects
    objects = [%Sphere{center: Vec3.vec3([4.0, 1.0, 0.0]), r: 1.0, material: %Metal{albedo: Vec3.vec3([0.7, 0.6, 0.5]), fuzz: 0.0}}]++objects
    objects
end

この球達を描画します。

次回

これでElixirのレイトレーサーができました。
次回は、これをFlowを使って並列化した上で、他言語やC++のCPU並列、GPU並列でベンチマークを取って性能比較を行います。