はじめに
以下の内容の個人的まとめ。
- リー代数を用いた微小回転の表現方法
- 回転行列の指数関数を用いた表現方法
参考資料
3次元回転に関して丁寧に解説されている本
金谷健一著 「3次元回転 ーパラメータKさんとリー代数による最適化」共立出版

こちらの本は非常に丁寧に書かれているので、ご購入されるとよいと思います。
以下ではこの本のことを回転本といいます。
その他資料
6.1 微分による回転の最適化
データの回転を推定するのに回転行列 ${\bf R}$ のある関数 $J({\bf R})$ を最小化する問題を考える。
四章、五章のように目的関数 $J({\bf R})$ が特殊な形 -> 特異値分解や四元数表示により求めることができる。
一方で、目的関数 $J({\bf R})$ が一般的な形は以下の2つが考えられる。
回転行列をパラメータ化する方法
関数 $J({\bf R})$ を回転行列のパラメータで表し、それを反復的に微分することで目的関数 $J({\bf R})$ を減少させる。
例)
- 勾配降下法
- 共役降下法
- ニュートン法
- ガウス・ニュートン法
- レーベンバーグ・マーカート法
微小回転をパラメータ化する方法(リー代数的な方法)
回転行列をパラメータ化せず、微小回転をパラメータ化する。
関数 $J({\bf R})$ が最も減少するような微小回転を計算し、現在の回転 ${\bf R}$ に微小回転を加えることで更新する。これを反復する。
図を入れる
- この方法だとジンバルロックなどの特異点を気にする必要が無いらしい。
6.2 微小回転と角速度
微小回転の表現
まず回転行列 ${\bf R}$ がある軸の周りの微小な角度 $\Delta \Omega$ の回転を表すとする。
このとき回転行列 ${\bf R}$ は以下のテイラー展開ができるらしい。 ← どこから出てきた??
{\bf R} = {\bf I} + {\bf A} \Delta \Omega + O(\Delta \Omega)^2 \tag{6.1}
${\bf R}$ が直行行列である必要十分条件は P9 (2.5)式
{\bf RR}^{\top} = \cdots = {\bf I}\tag{2.5}
なので、
\begin{eqnarray}
{\bf RR}^{\top} &=& \left( {\bf I} + {\bf A} \Delta \Omega + O{(\Delta \Omega)}^2 \right) \left( {\bf I} + {\bf A} \Delta \Omega + O{(\Delta \Omega)}^2 \right)^{\top} \tag{6.2.1} \\
&=& \left( {\bf I} + {\bf A} \Delta \Omega + O{(\Delta \Omega)}^2 \right) \left( {\bf I}^{\top} + {\bf A}^{\top} \Delta \Omega + O{(\Delta \Omega)}^2 \right) \tag{6.2.2} \\
&=& {\bf I} + \left( {\bf A} + {\bf A}^{\top} \right) \Delta \Omega + O{(\Delta \Omega)}^2 \tag{6.2} \\
&=& {\bf I} \tag{6.2.3} \\
\end{eqnarray}
ここで(6.2.1)式から(6.2.2)式はtransposeの線形性を利用している。
(6.2)式と(6.2.3)式の関係から
\begin{eqnarray}
\left( {\bf A} + {\bf A}^{\top} \right) &=& O \\
\Leftrightarrow {\bf A}^{\top} &=& - {\bf A} \tag{6.3}
\end{eqnarray}
となり、${\bf A}$ は反対称行列となる。以下の計算も考慮して
{\bf A} =
\begin{pmatrix}
0 & -l_3 & l_2 \\
l_3 & 0 & -l_1 \\
-l_2 & l_1 & 0
\tag{6.4}
\end{pmatrix}
とおく。つまり
\begin{eqnarray}
{\bf R} =
{\bf I}
+
\begin{pmatrix}
0 & -l_3 & l_2 \\
l_3 & 0 & -l_1 \\
-l_2 & l_1 & 0
\end{pmatrix}
\Delta \Omega + O{(\Delta \Omega)}^2 \\
\end{eqnarray}
ベクトル ${\bf a} = (a_i)$ をこの微小回転で ${\bf a}'$ に移してみる。
\begin{eqnarray}
{\bf a}' &=& \left( {\bf I} + {\bf A} \Delta \Omega + O{(\Delta \Omega)}^2 \right) {\bf a} \tag{6.5.1}\\
&=& {\bf I}\cdot {\bf a} + {\bf A}\cdot {\bf a} \Delta \Omega + O{(\Delta \Omega)}^2 {\bf a} \tag{6.5.2}\\
&=& {\bf a} +
\begin{pmatrix}
0 & -l_3 & l_2 \\
l_3 & 0 & -l_1 \\
-l_2 & l_1 & 0
\end{pmatrix}
\begin{pmatrix}
a_1 \\
a_2 \\
a_3
\end{pmatrix}
\Delta \Omega + O{(\Delta \Omega)}^2 \tag{6.5.3} \\
&=& {\bf a} +
\begin{pmatrix}
l_2 a_3 - l_3 a_2 \\
l_3 a_1 - l_1 a_3 \\
l_1 a_2 - l_2 a_1
\end{pmatrix}
\Delta \Omega + O{(\Delta \Omega)}^2 \tag{6.5.4} \\
&=& {\bf a} + {\bf l} \times {\bf a} \Delta \Omega + O{(\Delta \Omega)}^2 \tag{6.5}
\end{eqnarray}
(6.5.4)式から(6.5)式において
{\bf l} =
\begin{pmatrix}
l_1 \\
l_2 \\
l_3
\end{pmatrix}
とおいている。
幾何学的な関係と角速度
これを図示するとこんな感じか。
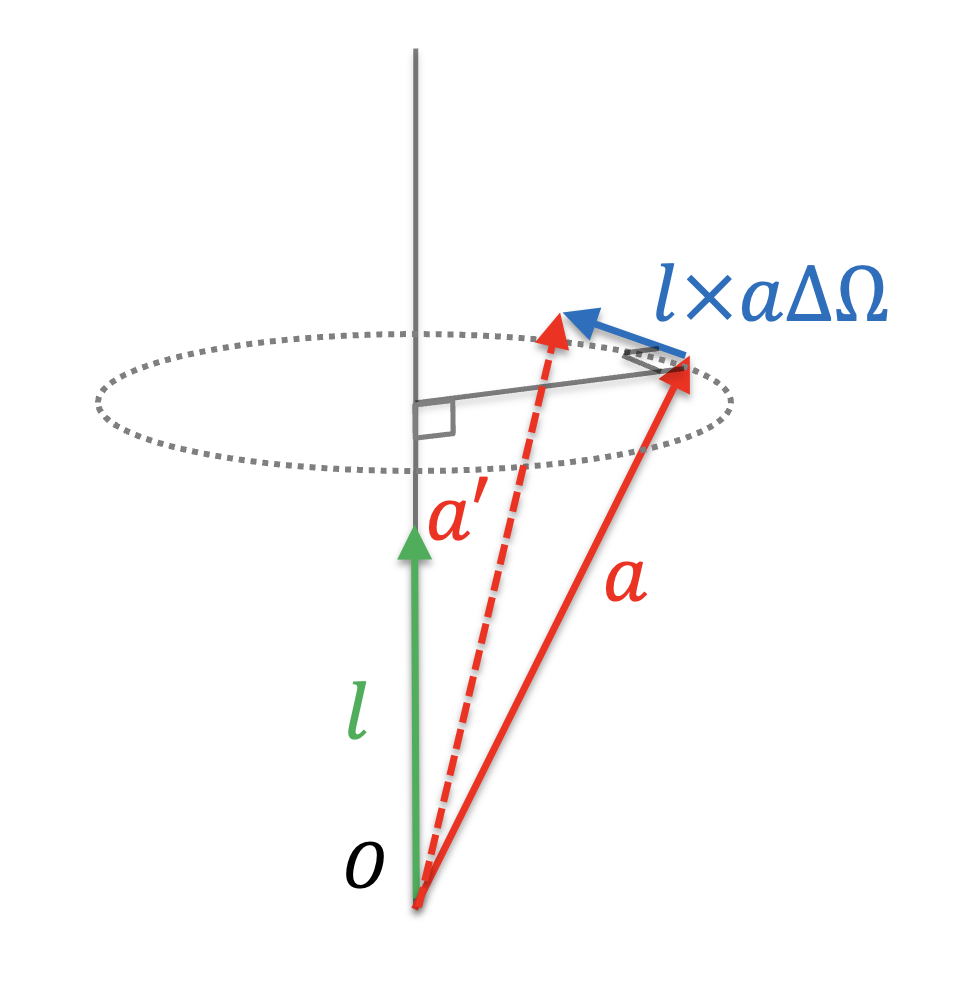
- まず ${\bf l}$ と ${\bf a}$ がある。
- これらの外積となる ${\bf l} \times {\bf a}$ 方向に微小な長さ $\Delta \Omega$ となる ${\bf l} \times {\bf a} \Delta \Omega$ がある。
- ${\bf a}$ に ${\bf l} \times {\bf a} \Delta \Omega$ を足したものが ${\bf a}'$ となる。
そうすると、${\bf a}$ は回転軸 ${\bf l}$ の接線方向にちょっとだけ移動して、${\bf a}'$ となるイメージ。この「ちょっと」をどんどん微小化すると接線は円弧に近似できるだろう。
-> なので微分を考える。
$\Omega$ を時間 $t$ の関数と考えて、${\bf a}$ の速度ベクトル ${\bf \dot{a}}$ を考える。
\begin{eqnarray}
{\bf \dot{a}} &=& \lim_{\Delta t \rightarrow 0} \frac{{\bf a}' - {\bf a}}{\Delta t} \tag{6.6.1}\\
&=& \lim_{\Delta t \rightarrow 0} \frac{{\bf a} + {\bf l} \times {\bf a} \Delta \Omega + O{(\Delta \Omega)}^2 - {\bf a}}{\Delta t} \tag{6.6.2}\\
&=& \lim_{\Delta t \rightarrow 0} \frac{{\bf l} \times {\bf a} \Delta \Omega + O{(\Delta \Omega)}^2}{\Delta t} \tag{6.6.3}\\
&=& \lim_{\Delta t \rightarrow 0} \frac{{\bf l} \times {\bf a} \Delta \Omega}{\Delta t} \tag{6.6.4}\\
&=& \lim_{\Delta t \rightarrow 0} \frac{ \Delta \Omega}{\Delta t} {\bf l} \times {\bf a} \tag{6.6.5}\\
&=& \omega {\bf l} \times {\bf a} \tag{6.6} \\
&=& {\bf \omega} \times {\bf a} \tag{6.8} \\
\end{eqnarray}
$\omega$ は単位時間の回転角なので角速度といえる。
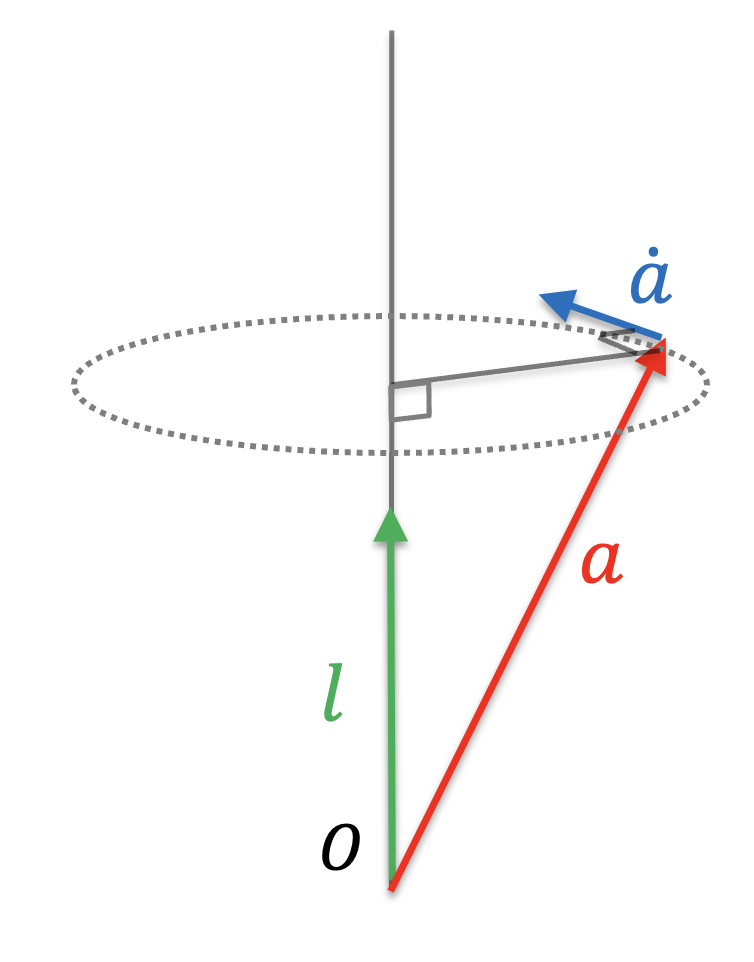
l が単位ベクトルであること
以下は用確認!
$\dot{a}$ は速度ベクトルなので
v = r \omega
から
\| {\bf \dot{a}} \| = \omega \| {\bf a} \| \sin \theta
一方で、(6.6)式から
\| {\bf \dot{a}} \| = \omega \| {\bf l} \| \| {\bf a} \| \sin \theta
よって
\| {\bf l} \| = 1
となり、${\bf l}$ は単位ベクトルとなる。
6.3 回転の指数関数表示
${\bf R_l}(\Omega)$: 回転軸 ${\bf l}$ 周りの角度 $\Omega$ の回転行列
回転行列 ${\bf R_l}(\Omega)$ を角度 $\Omega$ で微分する。
\begin{eqnarray}
\frac{d {\bf R_l}(\Omega)}{d \Omega} &=& \lim_{\Delta \Omega \rightarrow 0} \frac{{\bf R_l}(\Omega + \Delta \Omega) - {\bf R_l}(\Omega)}{\Delta \Omega} \\
&=& \lim_{\Delta \Omega \rightarrow 0} \frac{{\bf R_l}(\Delta \Omega){\bf R_l}(\Omega) - {\bf R_l}(\Omega)}{\Delta \Omega} \\
&=& \lim_{\Delta \Omega \rightarrow 0} \frac{{\bf R_l}(\Delta \Omega) - {\bf I}}{\Delta \Omega} {\bf R_l}(\Omega) \\
&=& \lim_{\Delta \Omega \rightarrow 0} \frac{{\bf I} + {\bf A} \Delta \Omega + O{(\Delta \Omega)}^2 - {\bf I}}{\Delta \Omega} {\bf R_l}(\Omega) \\
&=& \lim_{\Delta \Omega \rightarrow 0} \frac{{\bf A} \Delta \Omega }{\Delta \Omega} {\bf R_l}(\Omega) \\
&=& {\bf A} {\bf R_l}(\Omega) \tag{6.9}\\
\end{eqnarray}
回転行列の微分は反対称行列との積となる。
2回微分は
\frac{d^2 {\bf R_l}(\Omega)}{d \Omega^2} = {\bf A} \frac{d {\bf R_l}(\Omega)}{d \Omega} = {\bf A}^2 {\bf R_l}(\Omega)
n 回微分は
\frac{d^n {\bf R_l}(\Omega)}{d \Omega^n} = {\bf A}^{n-1} \frac{d {\bf R_l}(\Omega)}{d \Omega} = {\bf A}^{n} {\bf R_l}(\Omega)
これらから ${\bf R_l}(\Omega)$ の $\Omega = 0$ 周りのテイラー展開は
\begin{eqnarray}
{\bf R_l}(\Omega) &=& {\bf I} + \left. \frac{d {\bf R}}{d \Omega} \right|_{\Omega = 0} \Omega +
\frac{1}{2 !} \left. \frac{d^2 {\bf R}}{d \Omega^2} \right|_{\Omega = 0} \Omega^2
+ \frac{1}{3 !} \left. \frac{d^3 {\bf R}}{d \Omega^3} \right|_{\Omega = 0} \Omega^3 + \cdots \\
&=& {\bf I} + {\bf A} {\bf R_l}(0) \Omega + \frac{1}{2!} {\bf A}^2 {\bf R_l}(0) \Omega^2 + \frac{1}{3!} {\bf A}^3 {\bf R_l}(0) \Omega^3 + \cdots \\
&=& {\bf I} + \Omega {\bf A} + \frac{\Omega^2}{2!} {\bf A}^2 + \frac{\Omega^3}{3!} {\bf A}^3 + \cdots \tag{6.11.1}
\end{eqnarray}
回転本の(6.11)は誤植か?
ここで $e^x$ の $x = 0$ 周りのテイラー展開が
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\inf}
なので、これを拡張して(?)
\begin{eqnarray}
{\bf R_l}(\Omega) &=& \cdots \\
&=& {\bf I} + \Omega {\bf A} + \frac{\Omega^2}{2!} {\bf A}^2 + \frac{\Omega^3}{3!} {\bf A}^3 + \cdots
&=& e^{\Omega {\bf A}}
\tag{6.12}
\end{eqnarray}
と表記する。また
\begin{eqnarray}
\Omega {\bf l} &=&
\Omega
\begin{pmatrix}
l_1 \\
l_2 \\
l_3
\end{pmatrix} \tag{6.13.1}\\
&=&
\begin{pmatrix}
\Omega l_1 \\
\Omega l_2 \\
\Omega l_3
\end{pmatrix} \tag{6.13.2}\\
&=&
\begin{pmatrix}
\Omega_1 \\
\Omega_2 \\
\Omega_3
\end{pmatrix} \tag{6.13.3}\\
&=& {\bf \Omega} \tag{6.13}
\end{eqnarray}
とする。
\begin{eqnarray}
\Omega {\bf A} &=&
\Omega
\begin{pmatrix}
0 & -l_3 & l_2 \\
l_3 & 0 & -l_1 \\
-l_2 & l_1 & 0
\end{pmatrix} \tag{6.15.1}\\
&=&
\begin{pmatrix}
0 & -\Omega l_3 & \Omega l_2 \\
\Omega l_3 & 0 & -\Omega l_1 \\
-\Omega l_2 & \Omega l_1 & 0
\end{pmatrix} \tag{6.15.2}\\
&=&
\begin{pmatrix}
0 & -\Omega_3 & \Omega_2 \\
\Omega_3 & 0 & -\Omega_1 \\
-\Omega_2 & \Omega_1 & 0
\end{pmatrix} \tag{6.15.3}\\
&=&
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -\Omega_1 \\
0 & \Omega_1 & 0
\end{pmatrix}
+
\begin{pmatrix}
0 & 0 & \Omega_2 \\
0 & 0 & 0 \\
-\Omega_2 & 0 & 0
\end{pmatrix}
+
\begin{pmatrix}
0 & -\Omega_3 & 0 \\
\Omega_3 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix} \tag{6.15.4}\\
&=& \Omega_1
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{pmatrix}
+ \Omega_2
\begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0
\end{pmatrix}
+ \Omega_3
\begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix} \tag{6.15.5}\\
&=& \Omega_1 {\bf A}_1 + \Omega_2 {\bf A}_2 +\Omega_3 {\bf A}_3 \tag{6.15}
\end{eqnarray}
と表記する。これにより回転行列は
{\bf R}({\Omega}) = e^{\Omega {\bf A}} = e^{\Omega_1 {\bf A}_1 + \Omega_2 {\bf A}_2 + \Omega_3 {\bf A}_3} \tag{6.16}
と表記する。
6.4 無限小回転のリー代数
生成子(generator)
今までの議論から無限小回転は
{\bf I} + {\bf A} + \delta t
とかける。${\bf A}$ の部分を生成子と呼ぶ。
生成子の代数系
代数系(algebra)・・・ベクトル空間に積を定義したもの
生成子のベクトル空間に以下の積(交換子積)を定義して代数系(algebra)とする。
[{\bf A}, {\bf B}] = {\bf A}{\bf B} - {\bf B}{\bf A}
リー括弧積の定義
2つの元を他の元に写像する演算が以下の3つを満たすとき、リー括弧積という。
またリー括弧積を積とする代数をリー代数という。
1. 反可換(anticommutative)
\begin{eqnarray}
[{\bf A}, {\bf B}] &=& -[{\bf B}, {\bf A}]
\end{eqnarray}
2. 双線形(bilinear)
各変数に関して線形ということ。
\begin{eqnarray}
[{\bf A} + {\bf B}, {\bf C}] &=& [{\bf A}, {\bf C}] + [{\bf B}, {\bf C}] \\
[c{\bf A}, {\bf B}] &=& c [{\bf A}, {\bf B}] \\
\end{eqnarray}
3. ヤコビの恒等式
\begin{eqnarray}
[{\bf A} [ {\bf B}, {\bf C}]] + [{\bf B} [ {\bf C}, {\bf A}]] + [{\bf C} [ {\bf A}, {\bf B}]] = O \\
\end{eqnarray}
生成子による交換積がリー括弧積を満たすことの証明
1)反可換(anticommutative)を満たすことの証明
\begin{eqnarray}
[{\bf A}, {\bf B}] &=& {\bf A}{\bf B} - {\bf B}{\bf A} \\
&=& -({\bf B}{\bf A} - {\bf A}{\bf B}) \\
&=& -[{\bf B}, {\bf A}]
\end{eqnarray}
2)双線形(bilinear)を満たすことの証明
まず1つめ。
\begin{eqnarray}
(左辺)&=& [{\bf A} + {\bf B}, {\bf C}] \\
&=& ({\bf A} + {\bf B}){\bf C} - {\bf C}({\bf A} + {\bf B}) \\
&=& {\bf A}{\bf C} + {\bf B}{\bf C} - {\bf C}{\bf A} - {\bf C}{\bf B} \\
(右辺)&=& [{\bf A} {\bf C}] + [{\bf B}{\bf C}] \\
&=& {\bf A} {\bf C}-{\bf C} {\bf A} + {\bf B}{\bf C}-{\bf C}{\bf B} \\
\end{eqnarray}
よって成立。
次に2つ目
\begin{eqnarray}
[c{\bf A}, {\bf B}] &=& c {\bf A}{\bf B} - {\bf B} c {\bf A}\\
&=& c ({\bf A}{\bf B} - {\bf B} {\bf A})\\
&=& c [{\bf A}, {\bf B}] \\
\end{eqnarray}
よって成立。
行列の線形性から成り立つ。
3)ヤコビの恒等式を満たすことの証明
\begin{eqnarray}
[{\bf A} [ {\bf B}, {\bf C}]] + [{\bf B} [ {\bf C}, {\bf A}]] + [{\bf C} [ {\bf A}, {\bf B}]] &=&
{\bf A}({\bf B}{\bf C})-({\bf B}{\bf C}){\bf A} + {\bf B}({\bf C}{\bf A})-({\bf C}{\bf A}){\bf B}+{\bf C}({\bf A}{\bf B})-({\bf A}{\bf B}){\bf C} \\
&=&
{\bf A}{\bf B}{\bf C}-{\bf B}{\bf C}{\bf A} + {\bf B}{\bf C}{\bf A}-{\bf C}{\bf A}{\bf B}+{\bf C}{\bf A}{\bf B}-{\bf A}{\bf B}{\bf C} \\
&=& O
\end{eqnarray}
行列のassociativityから成り立つ。よって生成子(無限小回転)の交換積はリー括弧積であり、生成子(無限小回転)の集合はリー代数。
交換子積を基底に分解
生成子 ${\bf A}$ は
{\bf A} =
\begin{pmatrix}
0 & -l_3 & l_2 \\
l_3 & 0 & -l_1 \\
-l_2 & l_1 & 0
\end{pmatrix}
と3つの変数でかけるので自由度は3。
基底は
{\bf A}_1 =
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{pmatrix} ,
{\bf A}_1 =
\begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0
\end{pmatrix}
, {\bf A}_3 =
\begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix}
の3つ。(なぜ?)
よってこの基底を用いて
\begin{eqnarray}
{\bf A} &=& \omega_1 {\bf A}_1 + \omega_2 {\bf A}_2 \omega_3 {\bf A}_3 \\
&=&
\omega_1
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{pmatrix}
+ \omega_2
\begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0
\end{pmatrix}
+ \omega_3
\begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix} \\
&=&
\begin{pmatrix}
0 & -\omega_3 & \omega_2 \\
\omega_3 & 0 & -\omega_1 \\
-\omega_2 & \omega_1 & 0
\end{pmatrix} \tag{6.25} \\
\end{eqnarray}
とかける。
基底間の性質
[{\bf A}_2, {\bf A}_3] = {\bf A}_1 , [{\bf A}_3, {\bf A}_1] = {\bf A}_2 , [{\bf A}_1, {\bf A}_2] = {\bf A}_3 \tag{6.24}
以下1つ目のみ証明。
\begin{eqnarray}
[{\bf A}_2, {\bf A}_3] &=& {\bf A}_2 {\bf A}_3 - {\bf A}_3 {\bf A}_2 \\
&=&
\begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix}
-
\begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0
\end{pmatrix}
\\
&=&
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 1 & 0
\end{pmatrix}
-
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{pmatrix} \\
&=&
\begin{pmatrix}
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{pmatrix} \\
&=& {\bf A}_1
\end{eqnarray}
となり、成立。他の2つも同様。
交換子積とベクトル積との関係
交換子積を成分で書くと
\begin{eqnarray}
[{\bf A} , {\bf A}'] &=&
\begin{pmatrix}
0 & -\omega_3 & \omega_2 \\
\omega_3 & 0 & -\omega_1 \\
-\omega_2 & \omega_1 & 0
\end{pmatrix}
\begin{pmatrix}
0 & -\omega_3' & \omega_2' \\
\omega_3' & 0 & -\omega_1' \\
-\omega_2' & \omega_1' & 0
\end{pmatrix} \\
&& -
\begin{pmatrix}
0 & -\omega_3' & \omega_2' \\
\omega_3' & 0 & -\omega_1' \\
-\omega_2' & \omega_1' & 0
\end{pmatrix}
\begin{pmatrix}
0 & -\omega_3 & \omega_2 \\
\omega_3 & 0 & -\omega_1 \\
-\omega_2 & \omega_1 & 0
\end{pmatrix} \\
&=&
\begin{pmatrix}
0 & -(\omega_1 \omega_2'-\omega_2 \omega_1) & \omega_3 \omega_1'-\omega_1 \omega_3 \\
\omega_1 \omega_2'-\omega_2 \omega_1 & 0 & -(\omega_2 \omega_3'-\omega_3 \omega_2) \\
-(\omega_3 \omega_1'-\omega_1 \omega_3) & \omega_2 \omega_3'-\omega_3 \omega_2 & 0
\end{pmatrix}
\end{eqnarray}
これはもとの $\omega_i、\omega_i'$ の成分部分が $\omega_j \omega_k' - \omega_k \omega_j'$ と対応するベクトル積となっている。
以下の議論はよくわからないので、貼り付け。

