はじめに
今年５月にarXivにあがった以下の論文
[1] C. Jin, et. al. "Deep CT to MR Synthesis using Paired and Unpaired Data"
https://arxiv.org/abs/1805.10790
をまとめてみた。
概要
- GANを使ってCT画像からMRI画像を生成するモデル
- CTとMRIのペアがあるものと、無いものを混ぜて学習する
- ペアのないものに関してはcycle-consistencyをとる
- ペアのあるものに関しては、さらに生成したMRIとペアのMRIとの差をとる
以下の図で左からCTの元画像、生成したMRI合成画像、ペアとなるMRI画像、ペアMRIと合成MRIとの差。
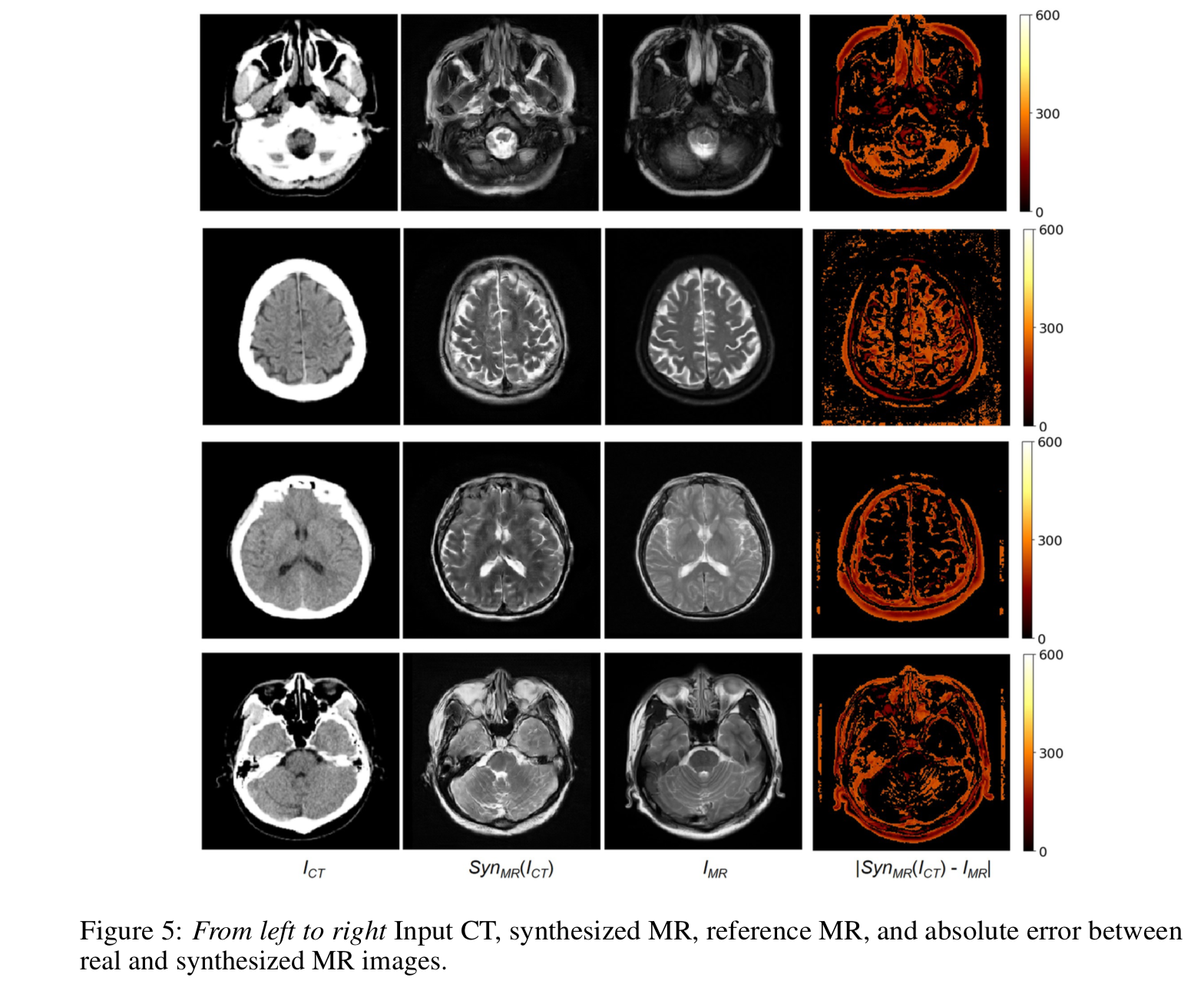[1] Figure 5 より
Architecture
CTとMRIのペアが無い場合
以下の図のように合成したMRIをdiscriminator に入れてadversarial なlossを取るのと同時に、cycle-GANごとく再合成したCT画像と元のCT画像とのcycle-consistencyをとる。
[1] Figure 3 より
CTとMRIのペアがある場合
以下の図のよう。上記のadversarial loss, cycle-consistency lossに加えてCT画像から生成したMRI画像と、CT画像のペアとなるMRI画像とのlossをとる。
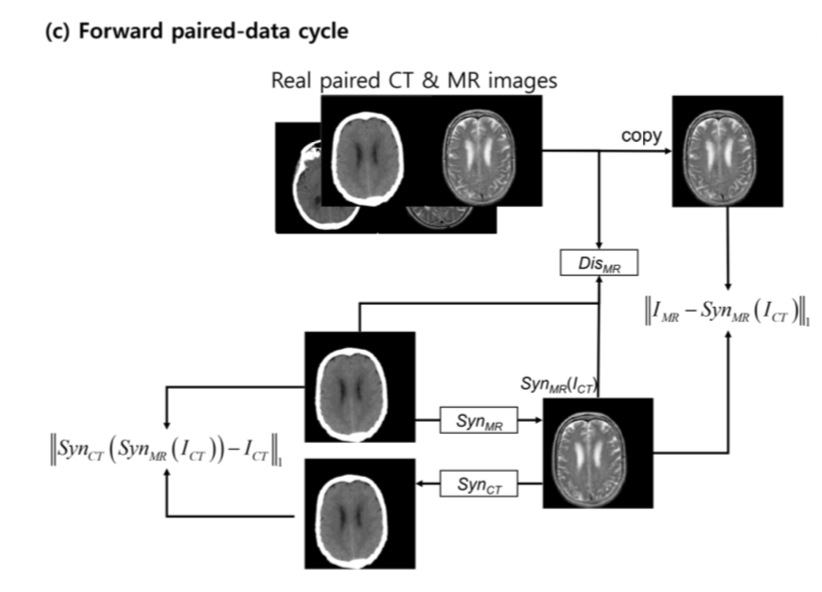
ここで discriminator はどうなってるの？という疑問が生じる。
ペアの画像もペアが無い単一の画像も同じ $Dis_{MR}$ に入れてるから。
実は以下のようになっている。
[1] Figure 4 より
つまり、中央のメイン部分は共有してるが、前段部分（Extra head）と出力部分（Extra tail）は別れている。
中央部のネトワークは共有するが、入口と出口でペアあり、ペアなしで異なる仕様となっている。
objective
adversarial な loss
\begin{eqnarray}
L_{GAN} (Syn_{MR}, Dis_{MR}, I_{CT}, I_{MR}) &=& \mathbb{E}_{I_{MR} \sim p_{data} (I_{MR})} [\log Dis_{MR} (I_{MR})] \\
&=& \mathbb{E}_{I_{CT} \sim p_{data} (I_{CT})} [\log (1 - Dis_{MR} (Syn_{MR}(I_{CT})))] \\
&=& \mathbb{E}_{I_{CT}, I_{MR} \sim p_{data} (I_{CT},I_{MR})} [\log Dis_{MR} (I_{CT},I_{MR})] \\
&=& \mathbb{E}_{I_{CT} \sim p_{data} (I_{CT})} [\log (1 - Dis_{MR} (I_{CT}, Syn_{MR}(I_{CT})))] \\
\end{eqnarray}
右辺１項目と２項目はペアが無い場合。
まず１項目はrealなMRをDiscriminatorに入れた場合。２項目はCTから合成したMRをDiscriminatorに入れた場合。
３項目はrealなMRとそのペアのCTをDiscriminatorに入れた場合。４項目はCTから合成したMRとそのペアのCTとをDiscriminatorに入れた場合。
また上記の式ではnegative log-liklihoodだが、実際はペアの無い方だけLSGANのleast squares lossを使う。（ペアのある方はnegative log-likelilhoodの方がよかったらしい）
つまり以下のように修正する。
\begin{eqnarray}
L_{GAN} (Syn_{MR}, Dis_{MR}, I_{CT}, I_{MR}) &=& \mathbb{E}_{I_{MR} \sim p_{data} (I_{MR})} [(Dis_{MR}(I_{MR}) - 1)^2] \\
&=& \mathbb{E}_{I_{CT} \sim p_{data} (I_{CT})} [(Dis_{MR}(Syn_{MR}(I_{CT})))^2] \\
&=& \mathbb{E}_{I_{CT}, I_{MR} \sim p_{data} (I_{CT},I_{MR})} [\log Dis_{MR} (I_{CT},I_{MR})] \\
&=& \mathbb{E}_{I_{CT} \sim p_{data} (I_{CT})} [\log (1 - Dis_{MR} (I_{CT}, Syn_{MR}(I_{CT})))] \\
\end{eqnarray}
cycle-consistency loss
cycle-consistency loss は以下。
\begin{eqnarray}
L_{dual-cyc} (Syn_{MR}, Syn_{CT}) &=& \mathbb{E}_{I_{CT} \sim p_{data} (I_{CT})} [\| Syn_{CT} (Syn_{MR} (I_{CT})) -I_{CT} \|_1] \\
&=& \mathbb{E}_{I_{MR} \sim p_{data} (I_{MR})} [\| Syn_{MR} (Syn_{CT} (I_{MR})) -I_{MR} \|_1] \\
&=& \mathbb{E}_{I_{CT}, I_{MR} \sim p_{data} (I_{CT}, I_{MR})} [\| Syn_{CT} (Syn_{MR} (I_{CT})) -I_{CT} \|_1] \\
&=& \mathbb{E}_{I_{MR},I_{CT} \sim p_{data} (I_{MR},I_{CT})} [\| Syn_{MR} (Syn_{CT} (I_{MR})) -I_{MR} \|_1] \\
\end{eqnarray}
右辺の１、２項目がペアが無いdataに関するもので、３、４項目がペアがあるdataに関するもの。
例えば１項目はCT画像からMR画像を合成し、それからCT画像を再合成した時の、それと元の画像とのL1 loss。
ペアとのL1 loss
ペアがあるものは合成したMRとペアのMRとでL1 lossをとる。
\begin{eqnarray}
L_{L1} (Syn_{MR}, Syn_{CT}) &=& \mathbb{E}_{I_{CT}, I_{MR} \sim p_{data} (I_{CT}, I_{MR})} [\| I_{MR} - Syn_{MR} (I_{CT}) \|_1] \\
&=& \mathbb{E}_{I_{MR},I_{CT} \sim p_{data} (I_{MR},I_{CT})} [\| I_{CT} - Syn_{CT} (I_{MR}) \|_1] \\
\end{eqnarray}
objective 全体
\begin{eqnarray}
L (Syn_{MR}, Syn_{CT}, Dis_{MR}, Dis_{CT}) &=& L_{GAN} (Syn_{MR}, Dis_{MR}, I_{CT}, I_{MR}) \\
&=& L_{GAN} (Syn_{CT}, Dis_{CT}, I_{MI}, I_{CT}) \\
&=& \lambda L_{dual-cyc} (Syn_{MR}, Syn_{CT}) \\
&=& \gamma L_{L1} (Syn_{MR}, Syn_{CT}) \\
\end{eqnarray}
この目的関数を以下のmin max ゲームで解く。
Syn^{*}_{MR} = \arg \min_{Syn_{MR}, Syn_{CT}} \max_{Dis_{MR}, Dis_{CT}} L(Syn_{MR}, Syn_{CT}, Dis_{MR}, Dis_{CT})
implementation
network
合成器（generator）のネットワーク構造は[2]のpoolingなしconvして、residual block、deconvする形。
その他、活性化関数はrelu、batch norm使う。
Discriminatorではpatch GAN（もしくはpix2pix）[3]ごとくNxN patchでlossをとる。
optimizerなど
- 最適化手法はAdam（learning rateは $2.0 \times 10^{-4}$ からはじめ減少させる）
- 目的関数のハイパーパラーメータは $\lambda = 10$ 、 $\gamma = 100$ 。
data augmentation
- horizontally flipping
- randomly cropped to 256x256 from 286x286
- rotated by $r \in [-5, 5]$ degrees
Metrics
以下の２種類でMRの合成を評価する。
mean absolute error
ペアのある画像に関して、L1 normで評価。
MAE = \frac{1}{N} \sum_{i=0}^{N-1} \| I_{MR} (i) - Syn_{MR} (I_{CT} (i)) \|
N はvoxel方向の数。つまりvoxel方向に平均をとる。
peak-signal-to-noise-ratio
また以下のpeak-signal-to-noise-ratio (PSNR) も用いる。
PSNR = 10 \dot \log_{10} \left( \frac{MAX^2}{MSE} \right) \\
MSE = \frac{1}{N} \sum_{i=0}^{N-1} ( I_{MR} (i) - Syn_{MR} (I_{CT} (i)) )^2
ただし $MAX = 255$ 。
まず２つ目の式でmean sqared errorを求める。これはvoxel内での平均的な合成MRとペアのMRとの差と考えられる。
これとmaximumな値との比率を１式で求める。
reference
[2] J. Johnson, et. al. "Perceptual losses for real-time style transfer and super-resolution"
[3] I. Zhu, et. al. "Image-To-Image Translation With Conditional Adversarial Networks" CVPR
書きかけ