はじめに
CCBR 2018より以下の論文
[1] S. Chen, et. al. "MobileFaceNets: Efficient CNNs for Accurate Real- Time Face Verification on Mobile Devices"
のまとめ
-
github:
pytorch実装
https://github.com/Xiaoccer/MobileFaceNet_Pytorch
tensorflow実装
https://github.com/sirius-ai/MobileFaceNet_TF
など
概要
- 顔認証を行うモデル
- 大型モデルと比較しても遜色ない精度を達成
- モバイル向けモデルと比較した際には精度を上回り、かつ2倍の推論速度を達成
- mobileNetを用いたモデルと比較した場合、最後のglobal average poolingをglobal depth-wise convolutionに替えていて、これが精度向上に寄与している
顔認証タスクにおける global average pooling の問題点
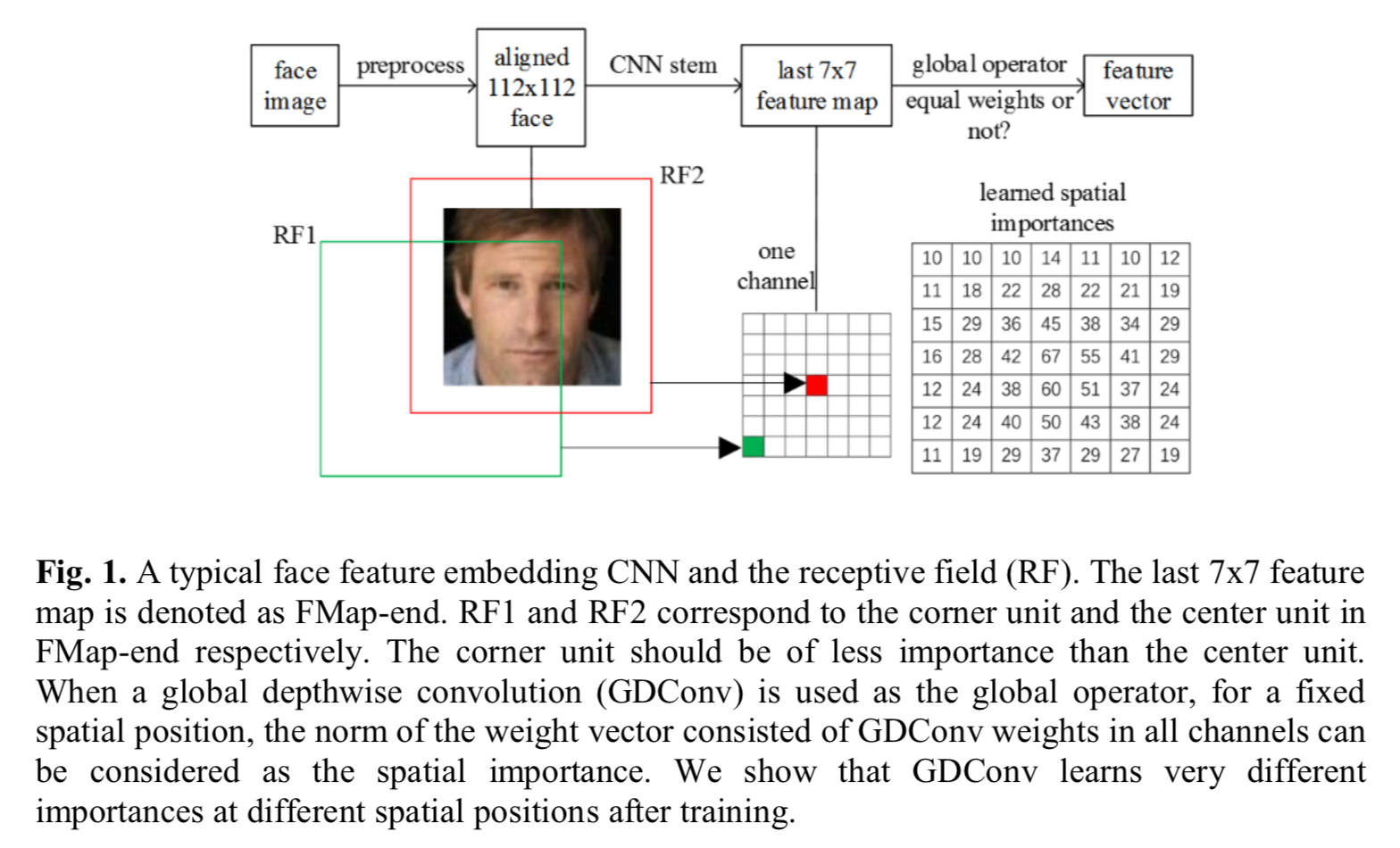
昨今のCNNでは出力前に global average pooling を使う場合が多い。しかし著者らに言わせると、こと顔認証においては問題がある。以下の図で
last 7x7のfeature mapにおいて、中央の赤いピクセルは、入力画像において赤い矩形領域が受容野となる。一方で、last 7x7 feature mapにおける緑のピクセルは、入力画像において緑の矩形領域が受容野となり、顔の一部を網羅していない。
そうすると、図中右下 learned spatial importance に示したように中央の値は重要(値が高く)なり、端付近は低くなる。そうすると、「チャンネルによっては顔の端付近の情報を得たい場合に、得られない」という問題が生じる??? -> ここ間違ってたら連絡ください
global depth-wise convolutionを使った解決法
上記問題に対して、本論文では global average poolingをfeature mapと同じサイズのkernel(つまり7x7)によってdepth-wise convすることで、対応している。
つまり出力 $G$ の $m$ 番目の値は入力のfeaturemap $F$ に対して
G_m = \sum_{i,j}K_{i,j,m} \cdot F_{i,j,m}
とする。
ネットワーク
ネットワークは以下。
基本は MobileNet なので、bottleneck 部分は depth-wise conv+point-wise convに対して residual なショートカットが加わった形。
loss
ArcFace[2]で提案されたArcFace lossを用いている。
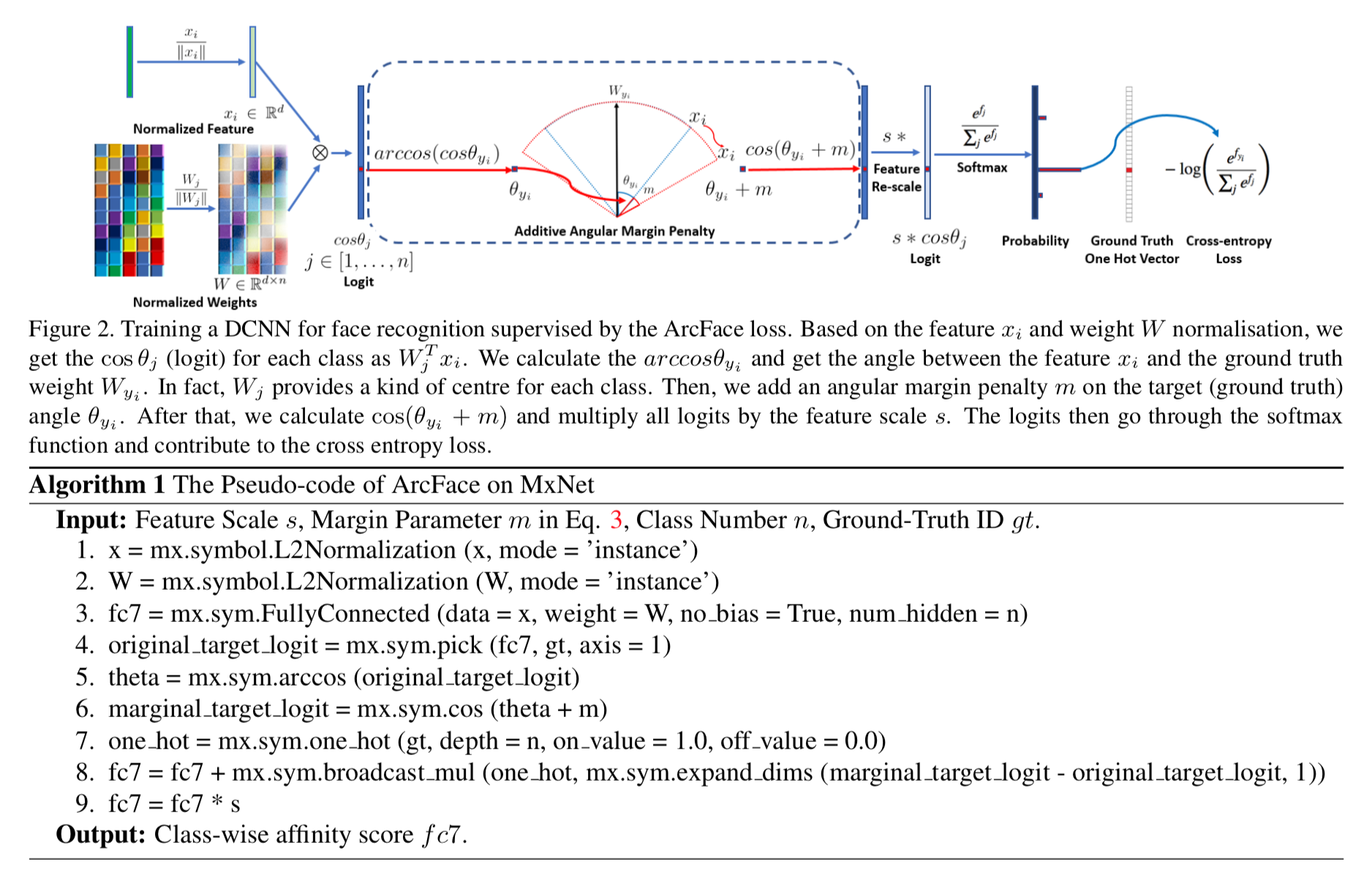
これはArcFace論文によると additive angular margin loss と言っていて、以下のようなもの。
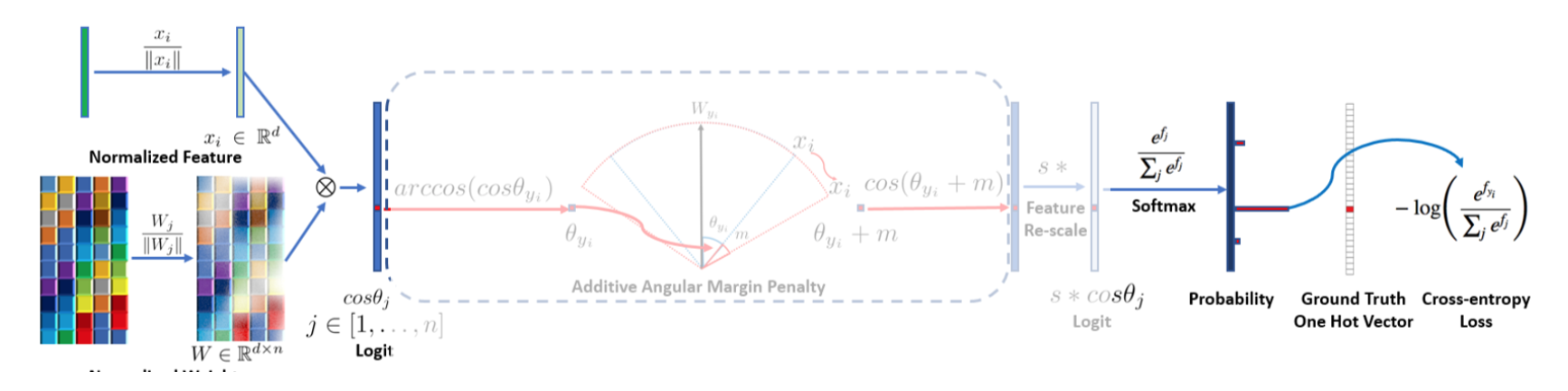
lossの全体像
まず、点線で囲われた Additive Angular Margin Penalty 抜きで考えてみる。
左上、モデルから出力された d 次元の特徴量が $x_i$。
これを正規化して $\frac{x_i}{| x_i |}$
一方で左下のように各クラス(行方向の n )の典型的な d 次元特徴量(列方向)を行列にした $W$を用意する。
これも各列 j に関して正規化しておく。つまり W の j 列目(クラス目)は $\frac{W_j}{| W_j |}$
この両者の内積を計算する。両者はもともと正規化されてるので、内積は j クラスのコサイン類似度のようなもの。
\cos \theta_j = \frac{x_i}{\| x_i \|} \cdot \frac{W_j}{\| W_j \|}
そうすると、コサイン類似度が高い j 列はモデルが最も確率が高いと予測した j クラスとなるので、softmaxを計算すると、確率が計算される。
これに対して通常のクラス分類ごとく target の one-hot ベクトルとで交差エントロピーを計算すればよい。
Additive Angular Margin Penalty な部分
これに対して、Additive Angular Margin Penalty は文字通り角度ベースでペナルティを加える。
具体的には、正解クラス $y_i$ に対して角度ベースでマージンを加え、結果的にコサインの値を小さくする。
\cos (\arccos (\cos \theta_{y_i}) + m)
そうすると、マージンを加えられてもsoftmaxで最大となるよう、$x_i$ をより代表ベクトルに近づけるよう学習するだろう。
実験と結果
他のmobile系のモデルとの精度、速度、パラメータ数の比較
datasetはLFW dataset, AgeDB-30 を用いて、以下の結果。
精度もスピードもよい
他の精度SOTAなモデルとのモデルサイズ・精度比較
LFW datasetを用いて他のSOTAな巨大モデルとの精度・パラメータ数を比較したものは以下。
ArcFace等、巨大モデルとも比肩する精度。
reference
[2] J. Deng, et. al. "ArcFace: Additive Angular Margin Loss for Deep Face Recognition"