はじめに
The Royal Society of Chemistry 2016から以下の論文
[1] T. Komatsu, et. al. "Image analysis for a microfluidic paper-based analytical Lab* color system".
本文:
https://pubs.rsc.org/en/content/articlehtml/2016/an/c6an01409g
supplemental materials:
https://www.rsc.org/suppdata/c6/an/c6an01409g/c6an01409g1.pdf
概要
- μPADの色をカメラで撮影して、そのpH値を読み取る類の論文
- phの推定方法としては、CIE Lab*空間上で基準点からの距離を用いる
- 従来のgrayscaleにおける判別法に比べて判断できるpHのレンジが広がった
手法
以下の手順で行う
1. μPADに各酸性度の水溶液とpH測定を行う試薬を注入する
以下のようなμPADを用いる。
説明にも書かれているが、detection zoneは 4 mm(φ) 、introduction zoneは 12 mm(φ)。
広い範囲でpHを測定するためpH指示薬は、チモールブルー(pKa1=1.7、pKa2=8.9、pH1.2~2.8、pH7.8~9.5)、メチルレッド(pKa=5.1、pH4.2~6.2)、ブロモチモールブルー(pKa=7.1、pH6.0~7.6)を混合して使用する。
まず、周辺のdetection zoneに各酸性度の水溶液を0.5μmL垂らす(計0.5 x 8 = 4.0μmL)。その後introduction zoneにpH指示薬を15μmL垂らす。各酸性度の水溶液が混じり合うことなくintroduction zoneに垂らしたpH指示薬は各detection zoneへいきわたるだろう。
2. カメラで撮影し、各色を取得する
蛍光灯下でデジタルカメラによりμPAD のデジタル画像を撮影する。その際、μPADとカメラとの距離は約20cmに固定する。色情報は、画像解析ソフト(ImageJ ver.1.48)を用いて取得する。
各pHの色は対応する各領域の平均値とする。
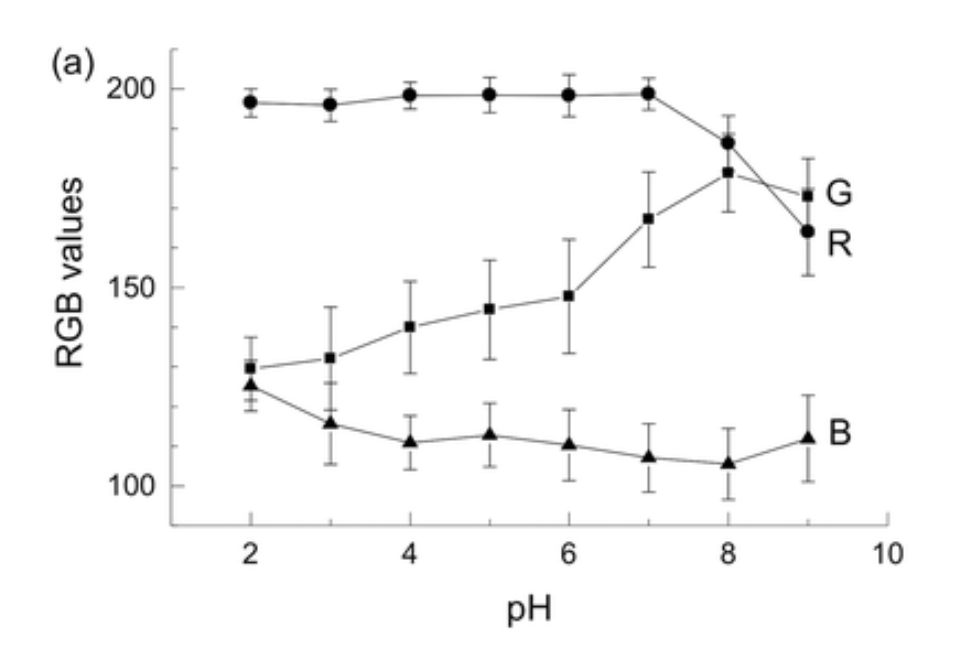
以下はpHの変化に対するRGB値の変化。
また以下は従来手法で提示されているgrayscale。
pHのレンジが広いため、pH変化に対して単調増加(もしくは単調減少)になっていない。
3. CIE Lab*空間上で距離の差分を計算し、pHを推定する
上掲のRGB値、grayscaleだと関数を何らかの形に落とし込むのは難しい。そこで CIE Lab*空間に落とし込む。
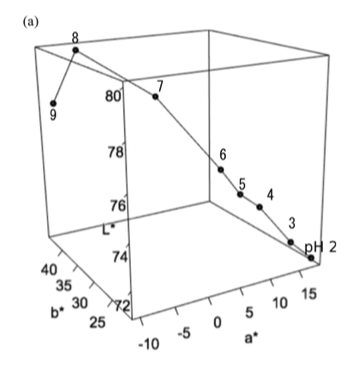
以下はLを鉛直方向、aを横、b*を奥にとったもの。
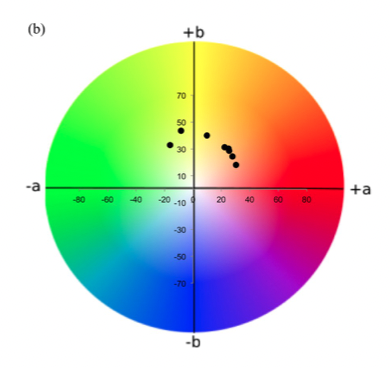
また以下はaとbを平面に図示したもの。回転角は単調に変化している、っぽい。
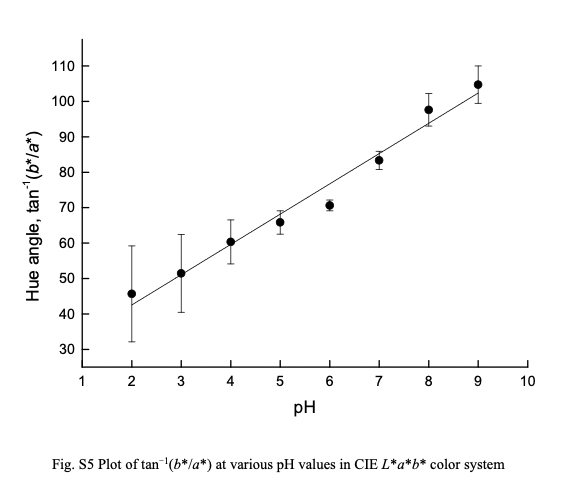
そこで以下のように横軸:ph、縦軸:回転角 $\arctan{(b/a)}$ にとる。
わりと直線的に変化する。よりフィッティングする関数を求めて、以下のようにCIE Lab*空間上における基準値からのユークリッド距離を計算する。
\Delta E = \sqrt{(a_x - a_0)^2 + (b_x - b_0)^2 + (L_x - L_0)^2} \tag{1}
右下添字は 0 が基準となる値を意味し、今回はpH=2。右下添字 x は対象のpHの値を意味する。
以下は横軸にpH、縦軸に $\delta E$ をとったもの。
sigmoid関数で近似させると $R^2 = 0.982$ となり、これは上掲の角度を直線で近似したものより当てはまりがいいらしい。(直線のR2は不明)
個人的感想
以下、門外漢が読んだ感想です。
- なぜpH-$\Delta E$ 関係の関数近似にsigmoid関数を用いたのか不明
- $\Delta E$ よりpH-角度関係を別の単調増加関数で表した方がよいのでは
まず1つ目に関して。例えば閉空間における生物の個体数 N の変化
\frac{dN}{dt} = rN \left( 1 - \frac{N}{K} \right)
のように、個体数の時間変化が個体数と環境の減少との積で表されるなら、ロジスティック関数(もしくはシグモイド関数)で表されるのは妥当だろう。
今回このような理論的背景があるかどうかは不明。たまたま単調増加かつ中央付近で下に凸から上に凸の変曲点があったのでsigmoidにしただけ?
次に2つ目に関して。そもそも色相が均等に変化するのが理想的なので、そうなるようにpH試薬の混合割合を調整するべき。そうするとpH - $\arctan{(b/a)}$ は直線的になるだろう。この方がスッキリする。