論文まとめ：Objects as Points

はじめに

• arXiv上の以下の論文（CenterNet）のまとめ
  [1] X. Zhou, et. al. "Objects as Points"

• arXiv:
  https://arxiv.org/pdf/1904.07850.pdf

• まとめ記事
  DeNAのざっくりしたまとめ：
  https://engineer.dena.jp/2019/07/cv-papers-19-keypoint-object-detection.html

• 著者らのコード
  Github:
  https://github.com/xingyizhou/CenterNet
  Pytorchっぽい。

journal等投稿先は不明。

概要

1. 2D、3Dのobject detectionやpose estimationで使えるしくみ
2. 物体の中央点をヒートマップで推定し、その関連情報も同時に推定する
3. そこそこの精度を保ちながらリアルタイムなスピードで処理できる

以下が手法をわかりやすくまとめた絵。

（[1] Figure2より）

物体の中心位置を赤い点のように推定する。出力のうち、矩形の縦チャンネル、横チャンネルからこの中心位置にあたるものを抜いてくればよい。

以下は推論速度と精度との関係図。

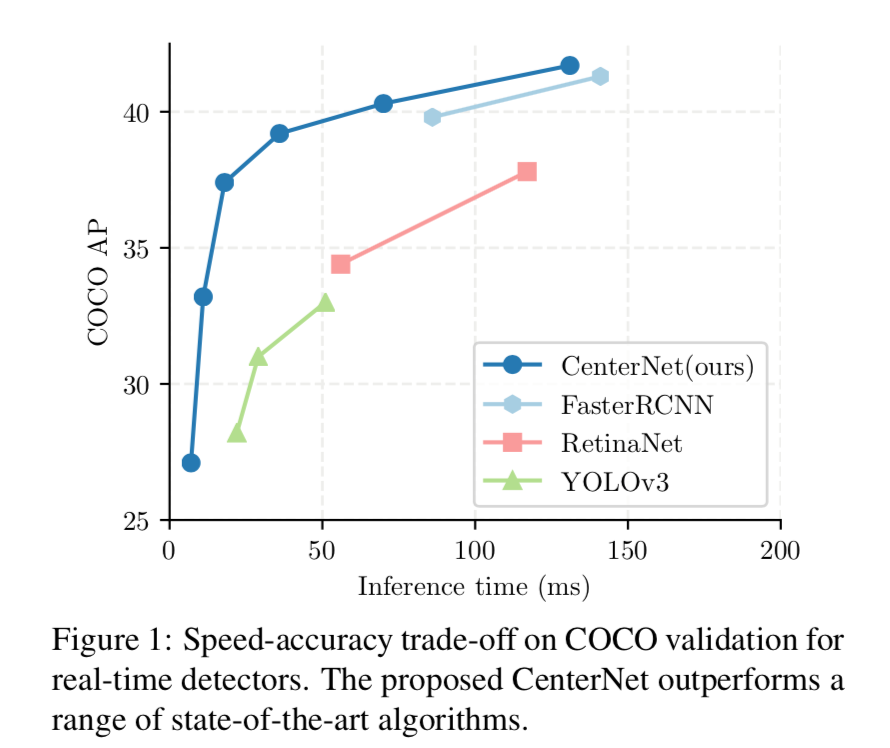
（[1]Figure1より）
YOLOやRetinaNetよりも更に左上に寄っている。

手法の解説

1. ヒートマップの作成

• $I \in R^{W \times H \times 3}$ ・・・入力画像
• $\hat{Y} \in [0,1]^{\frac{W}{R} \times \frac{H}{R} \times C}$ ・・・推定したheatmap。$R$ は縮小率。$C$ はheatmapの数。

骨格推定などと同様、ターゲットのheatmapはガウシアンカーネルで山形にする。

Y_{xyc} = \exp \left( - \frac{(x-\tilde{p}_x)^2 + (y-\tilde{p}_y)^2}{2 \sigma^2_p} \right)

$\tilde{p} = (\tilde{p}_x, \tilde{p}_y)$ は出力画像の大きさにおける物体中心点の座標。

$\sigma_p$ は物体ごとの標準偏差。これも骨格推定と同様だが、２つ以上のpeakによる重なりは最大値を採用する。

2. heatmapに関するLoss

heatmap に対するLoss は focal-loss。

L_k = \frac{-1}{N} \sum_{xyc} 
  \begin{cases}
    (1-\hat{Y}_{xyc})^{\alpha} \log (\hat{Y}_{xyc}) & if \ Y_{xyc} = 1 \\
    (1-\hat{Y}_{xyc})^{\beta} (\hat{Y}_{xyc})^{\alpha} \log (1-\hat{Y}_{xyc}) & otherwise  \\
  \end{cases}

$N$ は画像中のkeypointの数。

3. オフセットに関するloss

出力画像は大きさが $\frac{W}{R} \times \frac{H}{R}$ と粗くなってるので、heatmapのpeakを拾っても元の画像上の位置から微妙にずれてる可能性がある。そこでオフセット $\hat{O} \in \mathcal{R}^{\frac{W}{R} \times \frac{H}{R} \times 2}$ も推定させ、target のオフセットとの L1 で loss をとり、学習させる。

L_{off} = \frac{1}{N} \sum_p \left|\hat{O}_p - \left( \frac{p}{R} - \tilde{p} \right)  \right|   

4. bounding box の幅、高さに関する loss

各 $k$ チャンネルにおける bounding box は１つ推定する。その幅、高さを $w_k, h_k$ とすると、bounding box のサイズは $s_k = (w^{(k)}, h^{(k)})$ となる。

これの推論値 $\hat{S}_{p_k} \in \mathcal{R}^{\frac{W}{R} \times \frac{H}{R} \times 2}$ とで L1 をとり、lossとする。

L_{size} = \frac{1}{N} \sum^{N}_{k=1} \left| \hat{S}_{p_k} - s_k \right|

5. トータルの loss

トータルの loss： $L_{det}$ は以下。

L_{det} = L_k + \lambda_{size} L_{size} + \lambda_{off} L_{off}

ハイパーパラメータの $\lambda$ は $\lambda_{size} = 0.1$ と $\lambda_{size} = 1.$ を用いている。

6. 推論時のbounding box 推定手順

（１）各 $c$ チャンンルの heatmap におけて周辺８近傍のpeakを値が高いものから順に100個

\hat{P}_c = \left\{ (\hat{x}_{c,i}, \hat{y}_{c,i}) \right\}^{100}_{i=1}

拾う。

（２）中心はオフセットも考慮して $(\hat{x}_{c,i} + \delta \hat{x}_{c,i}, \hat{y}_{c,i} + \delta \hat{y}_{c,i})$ とする。

（３）矩形の座標は推定した $(\hat{w}_{c,i}, \hat{h}_{c,i})$ から

左上の座標は、

(\hat{x}_{c,i} + \delta \hat{x}_{c,i} - \frac{\hat{w}_{c,i}}{2}, \hat{y}_{c,i} + \delta \hat{y}_{c,i} - \frac{\hat{h}_{c,i}}{2})

、右下の座標は

(\hat{x}_{c,i} + \delta \hat{x}_{c,i} + \frac{\hat{w}_{c,i}}{2}, \hat{y}_{c,i} + \delta \hat{y}_{c,i} + \frac{\hat{h}_{c,i}}{2})

とする。

ニューラルネットのアーキテクチャ

４つのアーキテクチャを用いた。

1. ResNet-18
2. ResNet-101
3. DLA-34
4. Hourglass-104

３番目のDLAは知らなかったが、[2]で提案されたこのような

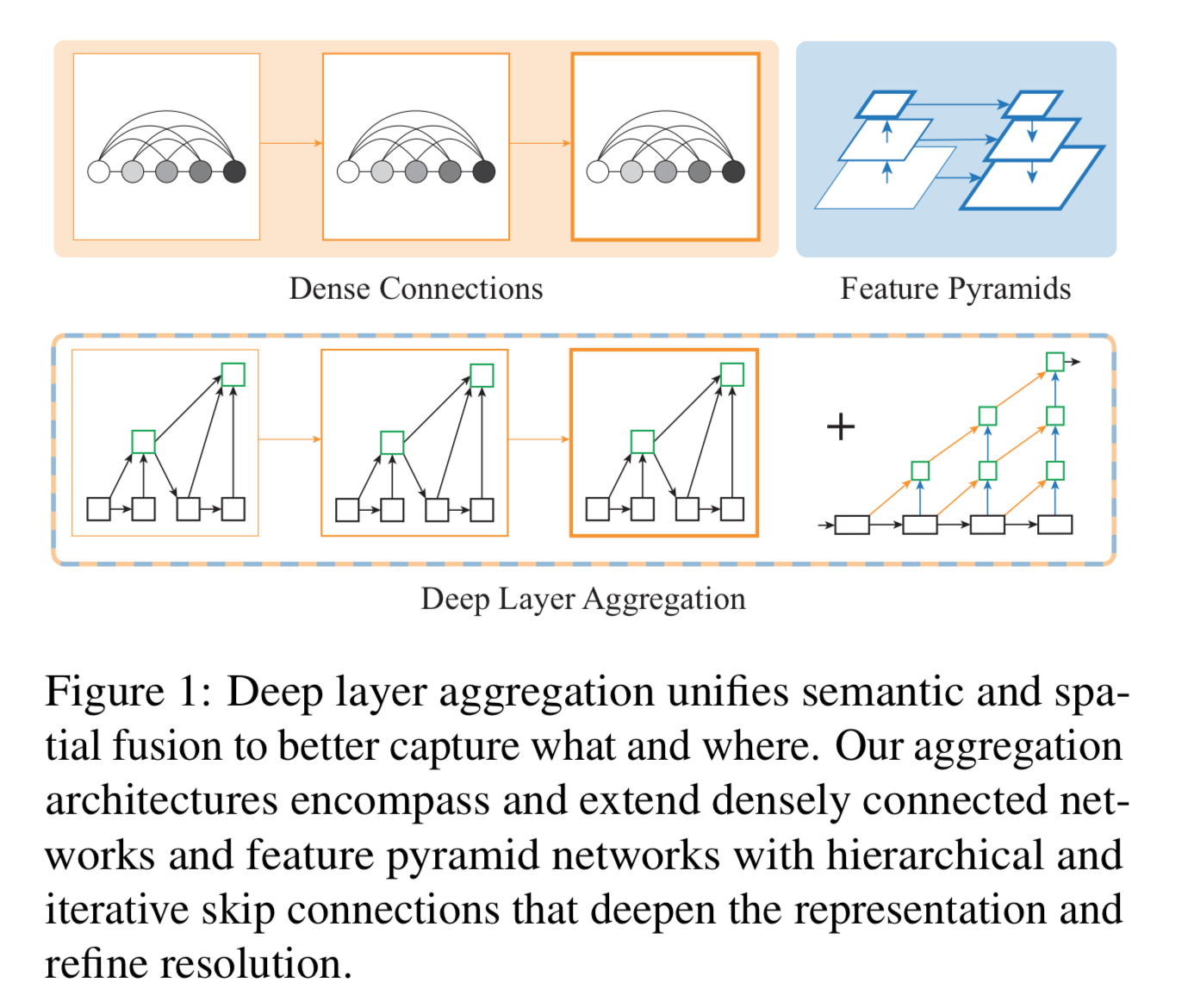（[2]Figure1より） ネットワーク。

実験と結果

1. ４つのネットワークで精度・速度を比較

MS COCO datasetで４つのアーキテクチャを比較したものが以下。

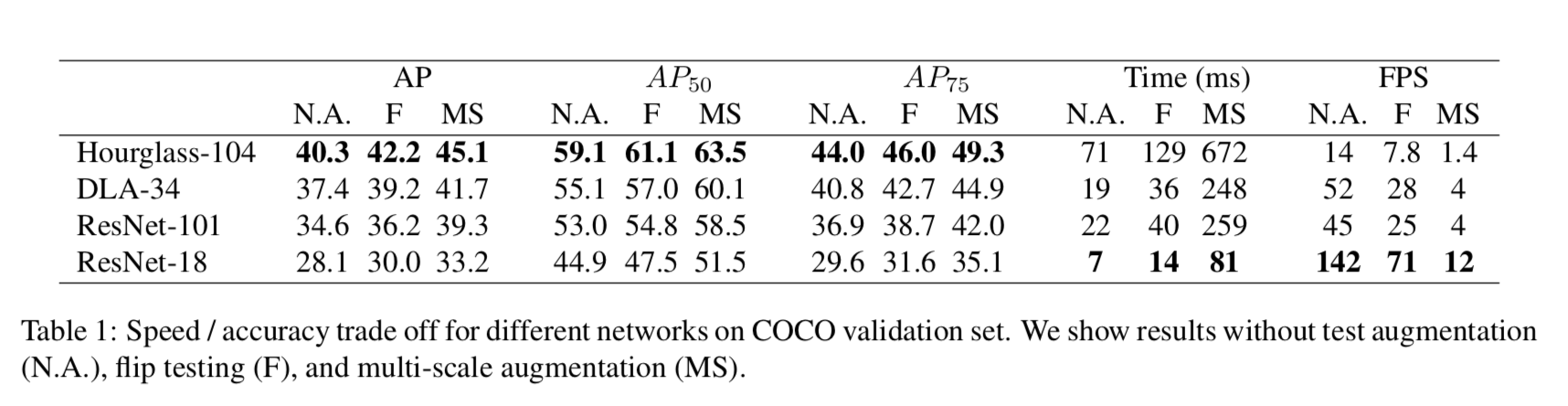
推論速度は軽いResNe-18が最速だが、精度は今流行りのHourglassがいい。

2. 他の有名モデルとの精度・速度の比較

MS COCO test dataset を用いて既存の有名モデルとの精度・速度の比較をした結果は以下。

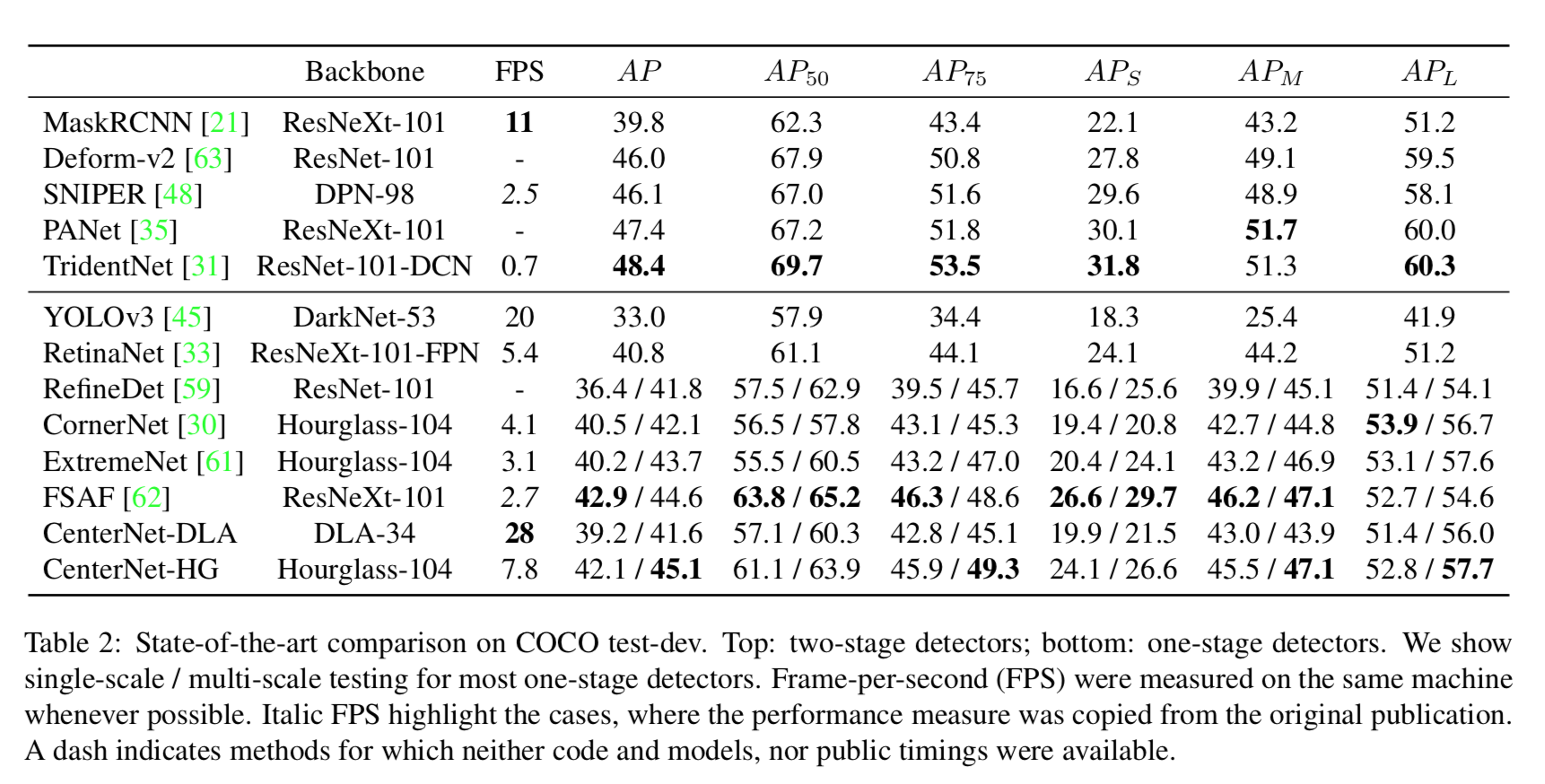
説明にも書いているが、CenterNet-DLAはDLAのアーキテクチャ、CenterNet-HGはhourglass。average precisionのスラッシュ左側がsingle scale、右がmulti scale。

FASF に比肩しうる精度でありながら3倍の推論速度となっている。

Reference

[2] F. Yu, et. al."Deep layer aggregation", CVPR 2018.