はじめに
ECCV 2020 から以下の論文
[1] Z. Wang, et. al. "Towards Real-Time Multi-Object Tracking". ECCV 2020.
のまとめ
-
略称
JDEモデル(Jointly learns the Detector and Embedding model)
例えばMOT16 dataset だと割とSOTAに近い結果。
https://paperswithcode.com/sota/multi-object-tracking-on-mot16
一部書きかけ
概要
- 同時に多数の人をトラッキングする(multi-object tracking)モデル
- detectionと特徴量抽出を同時に行う(1-shot)ことにより推論速度を上げた
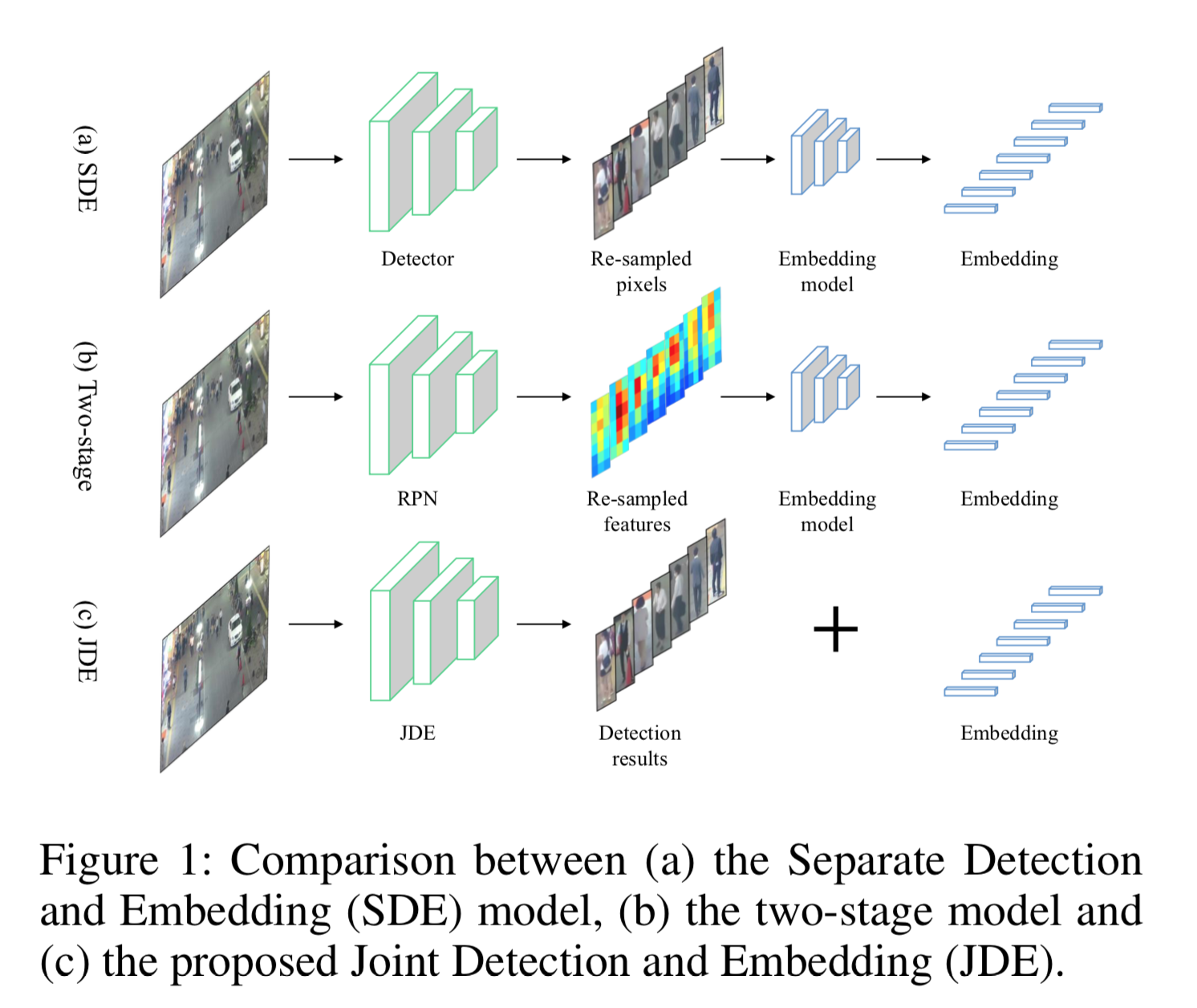
以下の図では上2つが既存の2-shot系モデル。下の本手法JDEはbounding boxと特徴量を同時に出す。
この論文の位置付けを考えるに、個人的には以下のような時代の流れ
1)2-shot系(detectionしてから、そこの特徴量を抽出する)
2)1-shot系のアンカーベース・・・本論文
3)1-shot系のアンカー無し・・・FairMOTモデル等
4)次のフレームもNNから予測・・・CenterTrack等
の中の2)あたりかなと。
ネットワークのアーキテクチャ
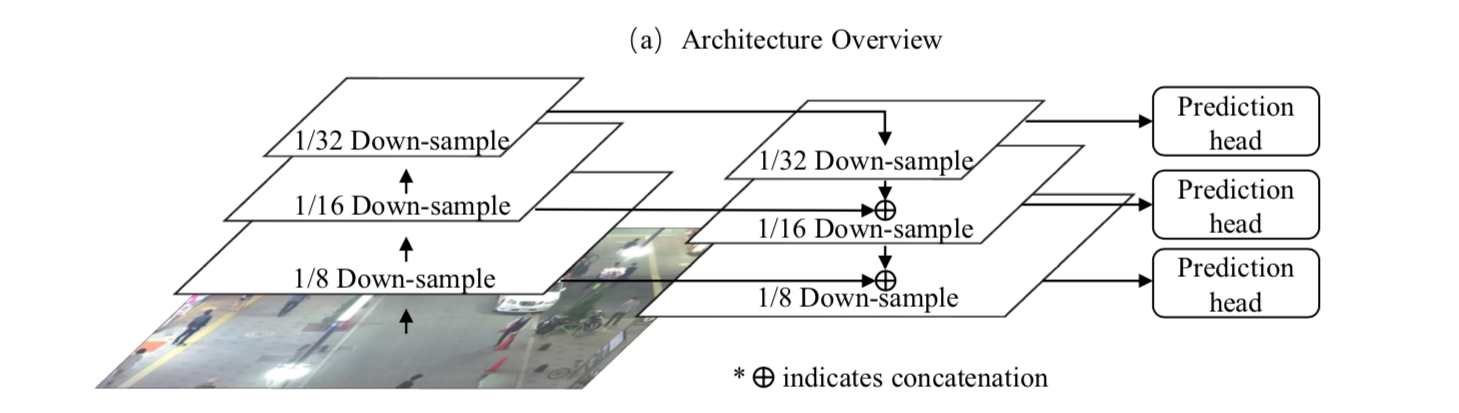
ネットワークのアーキテクチャは以下。
FPN系。
出力は以下の3種類
- 物体か物体でないかの識別
- bounding boxのサイズ
- 物体のembedding
Loss
1. 物体か物体でないかの識別に関する loss
識別問題なので交差エントロピー
2. bounding boxのサイズに関する loss
detection でよく用いられる smooth-L1 loss
3. 物体のembeddingに関する loss
まずアンカーとなる物体の特徴量を $f^{\top}$ 、それに対して異なるframeの同じ物体の特徴量を $f^{+}$ 、異なる人の特徴量を $f^{-}$ とする。
ベーシックなtriplet lossから考えると、
\mathcal{L}_{triplet} = \max (0, f^{\top}f^{-} - f^{\top}f^{+})
だが、tracking datasetには同じ人のシーンが少ないので、できるだけ利用するため
\mathcal{L}_{triplet} = \sum_i \max (0, f^{\top}f^{-}_i - f^{\top}f^{+})
とする。$f^{+}$ はミニバッチ内で最も難しい同一物体のサンプルで固定する。
だが、これだと収束が不安定かつ遅いので、以下の smooth upper bound of triplet lossにする。
L_{upper} = \log(1+ \sum_i \exp (f^{\top} f_i^{-} - f^{\top} f^{+} ))
ここで $f^{+}$ は固定なので変形して、
\begin{eqnarray}
L_{upper} &=& \log(1+ \exp(- f^{\top} f^{+} ) \sum_i \exp (f^{\top} f_i^{-}) ) \\
&=& \log \left( 1+ \frac{\sum_i \exp (f^{\top} f_i^{-})}{ \exp( f^{\top} f^{+} )} \right) \\
&=& \log \left( \frac{\exp(f^{\top} f^{+} ) + \sum_i \exp (f^{\top} f_i^{-})}{ \exp(f^{\top} f^{+} )} \right) \\
&=& - \log \left( \frac{ \exp(f^{\top} f^{+} )}{\exp(f^{\top} f^{+} ) + \sum_i \exp (f^{\top} f_i^{-})} \right) \\
\end{eqnarray}
と交差エントロピーっぽくなった。なので、最終的にはtriplet loss、smooth upper bound of triplet loss、交差エントロピーの3つを試している。
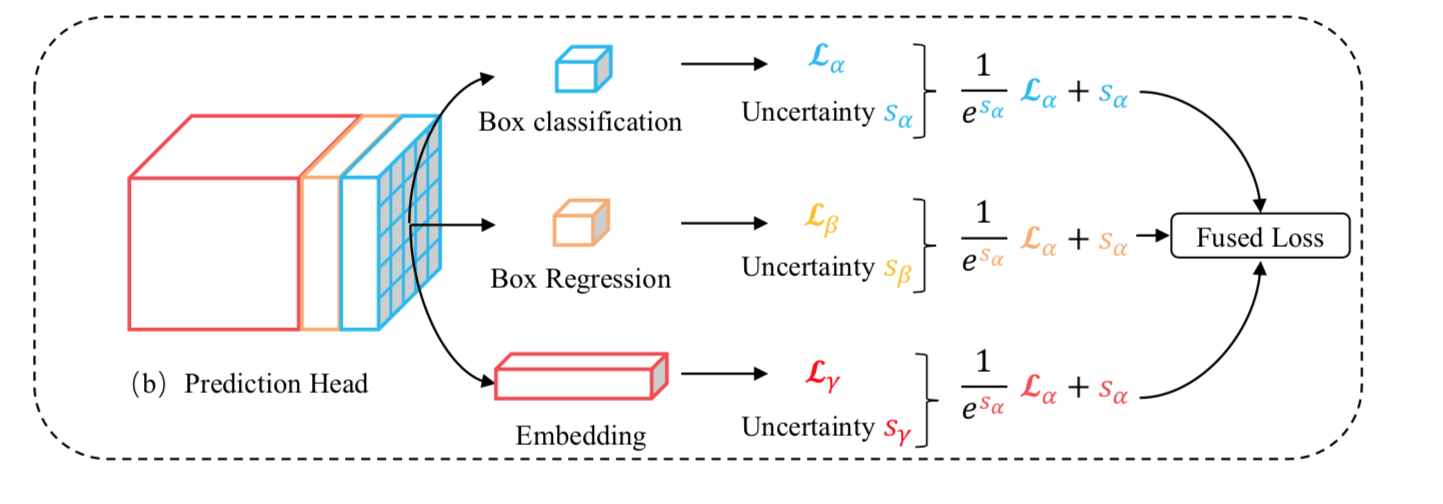
4. lossの掛け率を自動補正
書きかけ
マッチング
いわゆるトラッキングの第3行程、第4行程に関しては、Kalman Fileter、および Hangalian algorithmを用いる。
実験と結果
1. 他のモデルとの精度比較
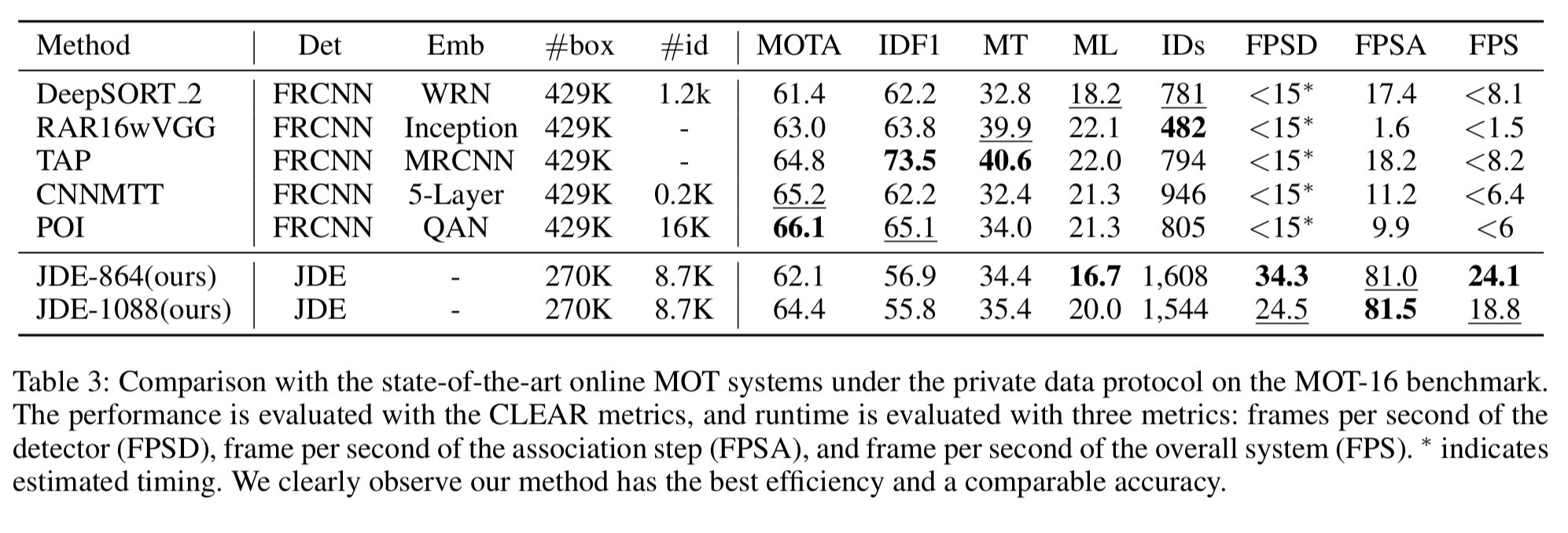
他のモデルとMOT-15 datasetでMOTAやFPS等を比較した図は以下。
2-shot系と比べて比肩しうる精度の上、速度はかなり優っている。
2. ablation study
書きかけ