はじめに
ICCV 2019 から以下の論文
[1] X. Nie, et. al. "Dynamic Kernel Distillation for Efficient Pose Estimation in Videos"
のまとめ
CVF open access:
http://openaccess.thecvf.com/content_ICCV_2019/papers/Nie_Dynamic_Kernel_Distillation_for_Efficient_Pose_Estimation_in_Videos_ICCV_2019_paper.pdf
arXiv:
https://arxiv.org/abs/1908.09216
コードの所在は不明
既に日本語のまとめ記事もある
https://engineer.dena.jp/2019/11/cv-papers-19-2d-human-pose-estimation.html#personlab
概要
- ビデオ中の各フレームに対して骨格推定を行うモデル
- Dynamic Kernel Distillation (DKD) module を使うことで高速に推論できる
- DKDでは前のフレームの情報を蒸留し、次のフレームにわたす
背景
ビデオから骨格推定する場合、従来手法では以下の図
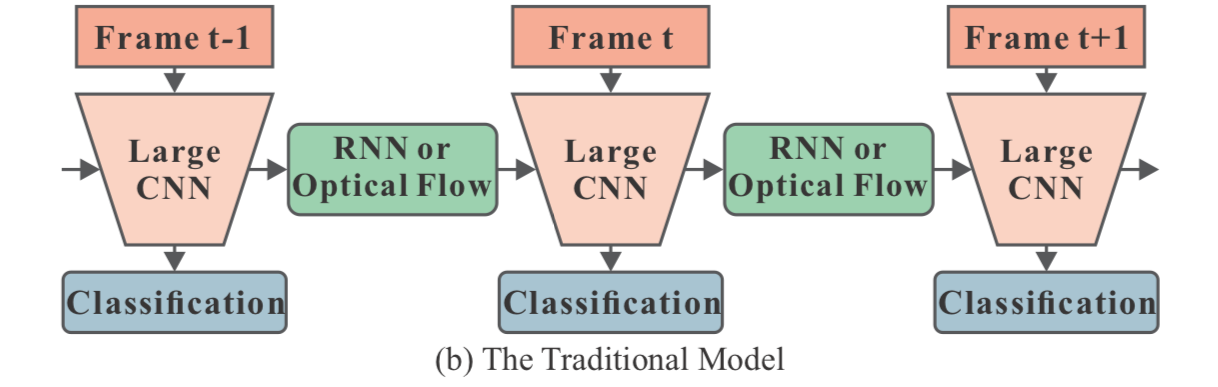（[1] Figure 1より）
のように大きなCNNから得た特徴量をRNNやoptical flow、あるいは3DCNNで次のフレームにわたしていた。
これらの手法は計算コストが大きいので、onlineで推論させるには厳しい。
提案手法
1. 各変数の定義
・ $\mathcal{V} = \left\{ I_t \right\} ^T_{t=1}$ ・・・$T$ フレームの画像 $I_t$ からなるビデオ $\mathcal{V}$
・ $I_t \in \mathbb{R}^{M \times N \times 3}$ ・・・高さ $M$ 、幅 $N$ の画像
・ $\mathcal{H} = \left\{ h_t \right\} ^T_{t=1}$ ・・・confidence map。
・ $h_t \in \mathbb{R}^{m \times n \times K}$ ・・・$K$ は関節の数
2. Pose Kernel distillation
Pose Kernel distillator は以下の図のように
（[1]Figure2より）
confidence map を蒸留させて、次のフレームにわたす役目。
具体的には以下のように
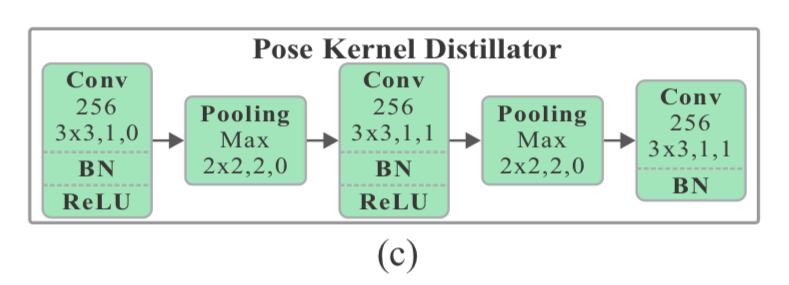（[1]Figure2より抜粋）
conv-bn-relu-poolingを２回やっている。
この Pose Kernel Distillator を $\Phi$ で表すと、Figure2のように feature map $f_t$ と confidence map $h_t$ を入力として、distill pose kearnels $k_t \in \mathbb{R}^{S \times S \times C \times K}$ を返す。（kearnelと呼ぶのは、後にこれを畳み込みのkernelとして使用するため）
k_t = \Phi (f_t, h_t)
$S$ はkernelのサイズ。
上図(c)を見てわかるように $\Phi$ は stride 2 のpoolingを２回やっているので、1/4（面積は1/16）に縮小されている。
よって $k_t$ はかなり小さくencodeされた骨格や特徴量的なもの。
これを次のフレームの feature map ： $f_{t+1}$ に対して畳み込む（ $\otimes$ ）ことにより、骨格の confidence map ： $h_{t+1}$ を生成する。
h^j_{t+1} = k^j_t \otimes f_{t+1}
ここで要注意なのは、畳み込みは骨格の種類 $j$ ごとに行われるということ。各関節では、$h^j_{t+1} \in \mathbb{R}^{m \times n}$ 、 $k^j_{t} \in \mathbb{R}^{S \times S \times C}$ 。
今一度、先ほどの図を見返すと、
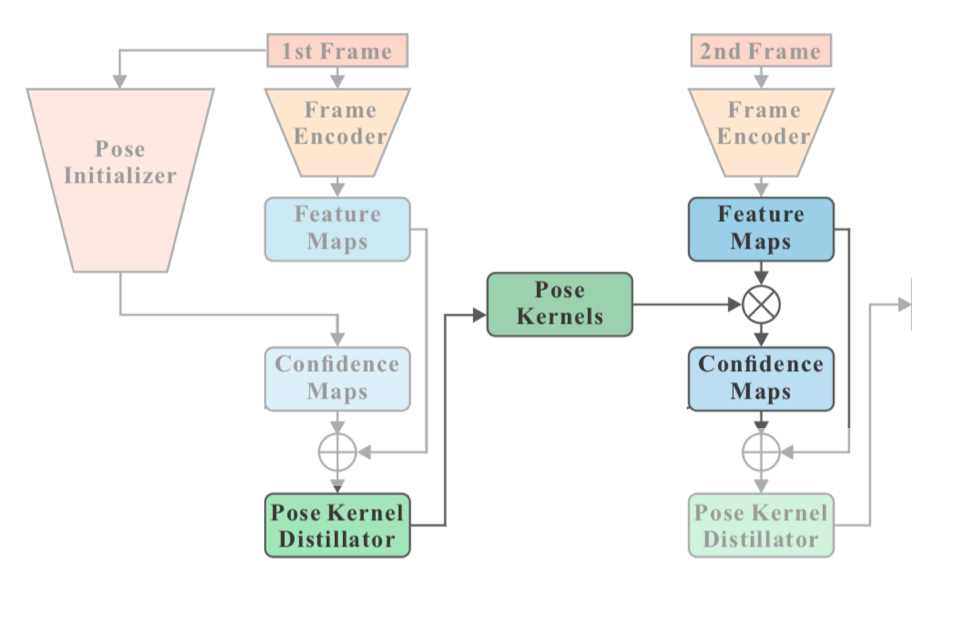
$t+1$ で feature map を畳み込むことで confidence map に変える kernel を $t$ の Pose Kernel Distillator で生成していることになる。
よくありがちな手法だと、前フレームの情報と現在の feature map をconcatenateして複数の畳み込み等を行なう、となるが、本手法は１回畳み込むだけなので高速。
Loss
loss は confidence map の target とMSEを計算することで求める。
\mathcal{L}_G = \sum^T_{t=1} \mathscr{l}_2 (h_t, \hat{h}_t)
なので図にするとこんな感じか。
Temporally adversarial training
さらに、adversarial な loss を取り入れることで、精度を上げている。具体的には、推論する confidence map の変化 $d_t = h_{t+1} - h_t$ が target の confidence map の変化 $\hat{d}_t = \hat{h}_{t+1} - \hat{h}_t$ に近くなるように discriminator で判別させる。
\mathcal{L}_D = \lambda \sum^{T-1}_{t=1} \mathscr{l}_2(d^f_t, d_t) - \sum^{T-1}_{t=1} \mathscr{l}_2(d^r_t, \hat{d}_t)
ここで
d^t_t = D(I_t, \hat{h}_t, I_{t+1}, \hat{h}_{t+1}) \\
d^f_t = D(I_t, h_t, I_{t+1}, h_{t+1})
これを
\min_{P, F, \Phi} \max_D \mathcal{L}_D
としてadversarialに学習すれば、discriminatorはrealなconfidence map ペアと実際の confidence mapの差が等しくなり、fakeなconfidence map ペアと実際のconfidence mapとの差が大きくなるように学習する。
一方で、P(Pose Initializer)とF(frame Encoder)、及び $\Phi$ （Pose Kernel Distillator) は推論した(fakeな）confidence map ペアに対してdiscriminatorがrealと判断するように（実際のconfidence mapとの差と同じくするように）学習する。
無理やり図にするとこんな感じか。
$\mathcal{L}_G$ も含めると以下。
\min_{P, F, \Phi} \max_D \mathcal{L}_G + \mu \mathcal{L}_D
今回ハイパーパラメータ $\mu$ は $0.1$ を用いた。
ネットワークのアーキテクチャ
まず、今回のネットワークは、以下の４つがある。
- Pose initializer
- Frame encoder
- Pose kernel distillator
- Temporally adversarial discriminator
1. Pose Initializer
これは[2]に出て来るU-shapeを模している。以下の図がそのアーキテクチャ。
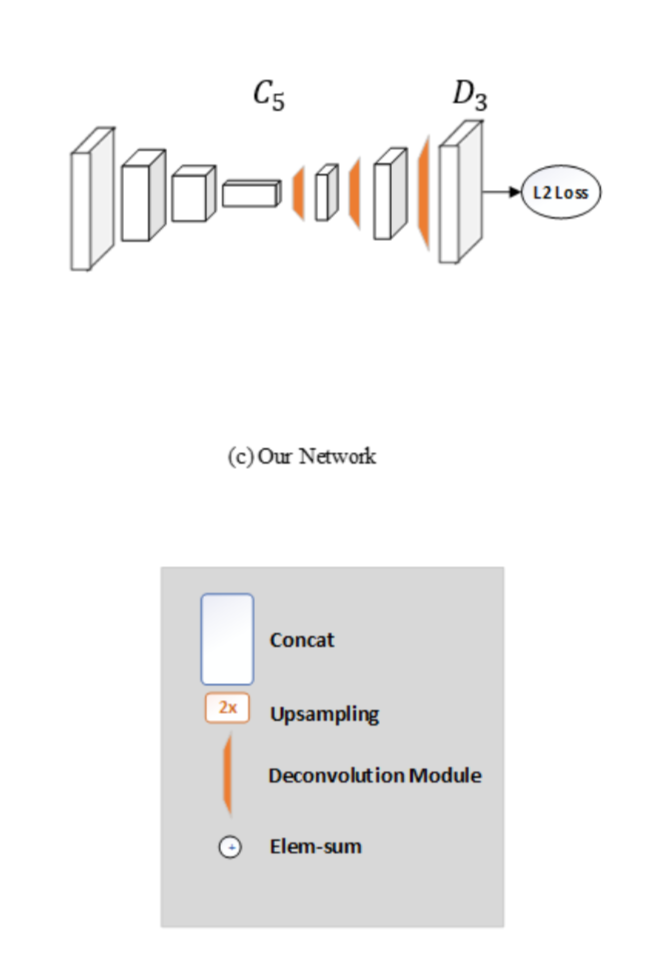（[2]Figure1より）
convしてdeconvする単純な構造。short-cutとかもない。
１つのブロックはresidual な blockにしてる。最終的には以下の図。
2. Frame encoder
これは Pose Initializer とほぼ同じ。推論速度重視なのでサイズは若干小さめ。
3. Pose kernel distillator
ここは再掲すると
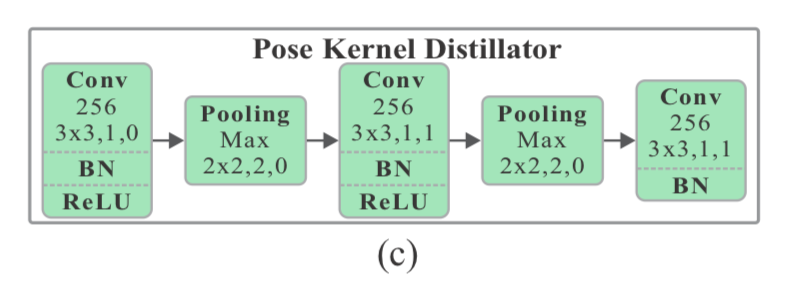（[1]Figure 2の(c)）
だが
書きかけ
reference
[2] B. Xiao, et. al. "Simple Baselines for Human Pose Estimation and Tracking"