はじめに
CVPR2017から以下の論文
[1] U. Iqbal, et. al. "PoseTrack: Joint Multi-Person Pose Estimation and Tracking"
のまとめ
同じ著者らの似た論文で CVPR2018に "PoseTrack: A Benchmark for Human Pose Estimation and Tracking"というものがあるが、こちらは名前の通りbenchmarkやsurveyに関する論文。
著者らの公式githubコード。
https://github.com/iqbalu/PoseTrack-CVPR2017
その他、同じCVPR2017でacceptされた有名論文で
[2] E. Insafutdinov, et. al. "ArtTrack: Articulated Multi-person Tracking in the Wild"
というものがある。
以下、主にロジック部分のみまとめ。
概要
- ビデオ映像の中の複数人に対して骨格の推定とtrackingを行うモデル
- 関節の候補位置を推定させ、それを時空間のグラフ問題として整数線形計画法で解く
以下の[1]Figure1のようにビデオ映像に対して骨格を推定する

モデル
モデルの全体像
以下の[1] Figure2で説明すると

まずはじめに、上段のようにビデオ映像の各フレームに対して関節(カラーの丸)を推定する。
次に中段のように、同じフレーム内でのある関節と別の関節との対応づけ(青線)、及びフレーム間に渡り同じ関節での対応づけ(赤線と黄色線)を行う。ここでは整数線形計画法を用いて最適化問題を解く。
最後に下段のようにそれらから各個人の骨格を推定する。
時空間グラフの構築
複数のフレームからなるビデオ $\mathcal{F}$ があり、各フレーム $f$ には任意の人が写っている。ビデオにおける関節候補 $D$ は、各フレーム $f$ における関節の候補 $D_f$ の全フレームにわたる集合。
D = \{D_f \}_{f\in\mathcal{F}}
また $\bf{x}\rm^f_d \in \mathbb{R}^2$ はフレーム $f$におけるある関節 $d \in D$ における座標。この $d$ はいずれかの関節タイプ $j \in \mathcal{J} = { 1, \cdots ,J }$ に属する。
本論文の課題である「多人数骨格トラッキング」は以下の時空間グラフ $G$
G = (D,E)
を推定する問題である。
ここで $E$ はedgesであり、任意の関節と関節とを結ぶ。これには2種類あって、同じフレームで空間的に結ぶ $E_s$ (例えばAさんの右肩とBさんの右肘)と、時間軸にわたって同じ関節を結ぶ $E_t$ (例えばフレーム3におけるAさんの右肩とフレーム4におけるAさんの右肩)がある。
つまり $E_s$ は
E_s = \cup_{f \in \mathcal{F}} E^f_s \ and \ E^f_s \{ (d,d'):d \neq d' \land d,d' \in D_f \}
で、$E_t$ は
E_t = \{ (d,d'):j = j' \land d \in D_f ,d' \in D_{f'} \land 1 \leq |f-f'| \leq \tau \land f, f' \in \mathcal{F} \}
である。
$1 \leq |f-f'| \leq \tau$ という制約があるので一定間隔以内のフレーム同士のみで考えている。隣同士のフレームのみでないのは、オクルージョンに対応するため。
グラフ分割
時空間グラフ $G$ には実際に関節ではない $D$ (以下nodesともいう)と、関係ないつながり(edges)・・・例えば同じフレーム内のAさんの右肩とBさんの左肩、あるいは異なるフレーム間でのAさんの右手とAさんの右足、など・・・が多数ある。このグラフを分割したい。
変数等の定義
そこで以下のバイナリー値を導入する。
\begin{eqnarray*}
v&\in& \{ 0,1 \}^{|D|}\\
s&\in& \{ 0,1 \}^{|E_s|}\\
t&\in& \{ 0,1 \}^{|E_t|}\\
\end{eqnarray*}
$v=0$ なら検出した関節候補は関節でないので削除する。
s_{(d_f, d'_f)}=0
また
t_{(d_f, d'_{f'})}=0
なら異なるフレーム間の時間的edgeである $(d_f, d'_{f'})$ は削除される。
目的関数
このグラフ分割は以下のコスト関数を最小化することにより達成する。
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\begin{eqnarray*}
&&\argmin_{v,s,t} (<v,\phi >+<s,\psi_s >+<t,\psi_t>) \\
&&<v,\phi> = \sum_{d \in D} v_d \phi(d) \\
&&<s,\psi_s > = \sum_{(d_f,d'_f) \in E_s} s_{(d_f,d'_f)} \psi_s (d_f, d'_f) \\
&&<s,\psi_t > = \sum_{(d_f,d'_{f'}) \in E_t} t_{(d_f,d'_{f'})} \psi_t (d_f, d'_{f'})
\end{eqnarray*}
ここで $\phi$ 、 $\psi_s$ 、 $\psi_t$ はそれぞれ
\begin{eqnarray*}
&&\phi(d) = \log \frac{1-p_d}{p_d} \\
&&\psi_s(d_f,d'_f) = \log \frac{1-p^s_{(d_f,d'_f)}}{p^s_{(d_f,d'_f)}} \\
&&\psi_t(d_f,d'_{f'}) = \log \frac{1-p^t_{(d_f,d'_{f'})}}{p^t_{(d_f,d'_{f'})}} \\
\end{eqnarray*}
$p_d \in (0,1)$ は予測した関節 $d$ の確率。$p^s$ はフレーム $f$ における $d$ と $d'$ の結合に関する確率。$p^t$ はフレーム $f$ における $d$ と フレーム $f'$ における $d'$ の結合に関する確率。
制約式
これらを整数線形計画法で解くが、そのときの制約は以下。
まず制約の1種類目。
s_{(d_f, d'_f)} \leq v_{d_f} \land s_{(d_f, d'_f)} \leq v_{{d'}_f} \ \ \ \forall (d_f,d'_f) \in E_s \\
t_{(d_f, d'_{f'})} \leq v_{d_f} \land t_{(d_f, d'_{f'})} \leq v_{{d'}_{f'}} \ \ \ \forall (d_f,d'_{f'}) \in E_t
上の式は同じフレーム $f$ において関節 $d_f$ と $d'_{f}$ がともに有効な時のみ両者の空間的 edge は有効とするもの。
下の式は異なるフレーム間の関節 $d_f$ と $d_{f'}$ 間において、それらが有効な時のみ両者の時間的 edge を有効とするもの。
次に制約の2種類目。
s_{(d_f, d'_f)} + s_{(d'_f, d''_f)} - 1 \leq s_{(d_f, d''_f)}\\
\forall (d_f, d'_f), (d'_f, d''_f) \in E_s
つまり以下の図のように
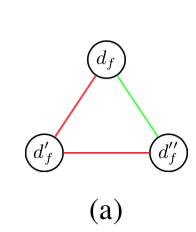
同じフレーム $f$ 内の3つの node に関して、2つの edge が有効なら、残りの1つの edge も有効とするもの。
同様に異なるフレーム間3つの node に関して、2つの edgeが有効なら、残りの1つの edge も有効とする。
t_{(d_f, d'_{f'})} + t_{(d'_{f'}, d''_{f''})} - 1 \leq t_{(d_f, d''_{f''})}\\
\forall (d_f, d'_{f'}), (d'_{f'}, d''_{f''}) \in E_t
図で書くとこう。
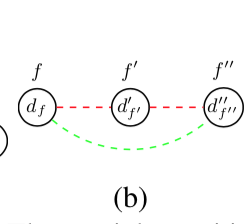
次の制約式は骨格が一定と想定するもの。
t_{(d_f, d'_{f'})} + t_{(d_{f}, d''_{f'})} - 1 \leq s_{(d'_{f'}, d''_{f'})}\\
t_{(d_f, d'_{f'})} + s_{(d'_{f'}, d''_{f'})} - 1 \leq t_{(d_{f}, d''_{f'})}\\
\forall (d_f, d'_{f'}), (d_{f}, d''_{f'}) \in E_t
最後の制約式は異なるフレーム間の4つの node に関するもの。
t_{(d_f, d'_{f'})} + t_{(d''_{f}, d'''_{f'})} + s_{(d_{f}, d''_{f})} - 2 \leq s_{(d'_{f'}, d'''_{f'})}\\
t_{(d_f, d'_{f'})} + t_{(d''_{f}, d'''_{f'})} + s_{(d'_{f'}, d'''_{f'})} - 2 \leq s_{(d_{f}, d''_{f})}\\
\forall (d_f, d'_{f'}), (d''_{f}, d'''_{f'}) \in E_t
んー、最後はややこしいな。