はじめに
BMVC 2018 から以下の論文のまとめ
A. Doering, et. al, "JointFlow: Temporal Flow Fields for Multi Person Pose Tracking"
arXiv:
https://arxiv.org/abs/1805.04596
コードの場所は不明
概要
- 単眼RGBビデオカメラからの映像から同時に複数人に対して姿勢推定・トラッキングを行うモデル
- real timeで行うことが可能
- 時間軸方向への関節の推移を表すベクトル場であるTFF(temporal flow fields) を用いる
以下がtrackingの例。

いずれもposetrack dataset に対する推論。上2つの行が車道のシーン、下2つの行がサッカーのシーン。
各列は左から右への時間推移だと思うが、同じ人に対して同じ色の骨格が塗られているので、同一の人物と推定されているだろう。
アーキテクチャ
アーキテクチャの全体像
以下の図が全体像。

1)左から t-1 時の画像 $I_{t-1}$ と t 時の画像 $I_t$ を入力する。
2)それぞれに対してCNNで特徴量を抽出する。
3)特徴量から各時間において関節の位置と四肢のベクトルを推定し、骨格を推定する。
4)一方で各時間における関節位置から関節の推移を推定する。
定義等
$p_j = (x_j, y_j)$ :関節 j の2次元座標
$P= \left\{ p_j \right\}_{i:J} $ :ある人の J 個ある関節群
$I_t$ : ビデオの t フレーム目の画像
$N_t$ :ビデオの t フレーム目の画像内における人の数
$\mathcal{P}_t = \{ P^{1}_t, \cdots , P^{N}t \}$ :t フレーム目の姿勢群
temporal flow fields
TFF(temporal flow fields) はこの論文の中核である。
中身は、OpenPoseのPAF(part affinity fields)とほぼ同じ。
PAFはあるフレーム内における関節 j から関節 j' への単位ベクトルを表す場だったが、TFFは t-1 フレームにおける関節 j から t フレームにおける関節 j への単位ベクトルを表す場に変わっただけ。
まず t フレームにおける k 番目の人の関節 j を
p^t_{j,k} \in P^k_t
で表す。単位ベクトル $\nu$ を k さんの j 関節におけるフレーム間の移動を正規化したものと考えると
\begin{eqnarray*}
\nu &=& \frac{p^t_{j,k} - p^{t-1}_{j,k}}{\| p^t_{j,k} - p^{t-1}_{j,k} \|_2}\\
&=& \frac{p^t_{j,k} - p^{t-1}_{j,k}}{\lambda_{j,k}}\\
\end{eqnarray*}
次に以下の図のように $\nu$ と垂直な $\nu_{\perp}$ を定義する。

以下のような領域 $\Omega_{j,k}$ を用いて、画像上の点 p がTFFに属する($p \in \Omega_{j,k}$)か否かを判別する。
\Omega_{j,k} = \left\{ p | 0 \leq \nu \cdot (p-p^{t-1}_{j,k}) \leq \lambda_{j,k} \land | \nu_{\perp} \cdot (p-p^{t-1}_{j,k}) | \leq \sigma \right\}
$\sigma$ はパラメータ。
つまり、$\Omega_{j,k}$ は

こんな感じの領域。この領域内に p が入る時に値を $\nu$ とし、他を0とする。
T^{*}_{j,k}(p) = \begin{cases}
\nu & if \ p \in \Omega_{j,k} \\
0 & otherwise.
\end{cases}
1チャンネルの feature map に全ての人の関節 j に関するTFF をのせるので、関節 j のTFF は
T^{*}_{j}(p) = \frac{1}{n_t (p)} \sum^K_{k=1} T^{*}_{j,k}(p)
となる。 $n_t (p)$ は non-zero となる $\nu$ の個数。
アーキテクチャの詳細
以下が詳細図。
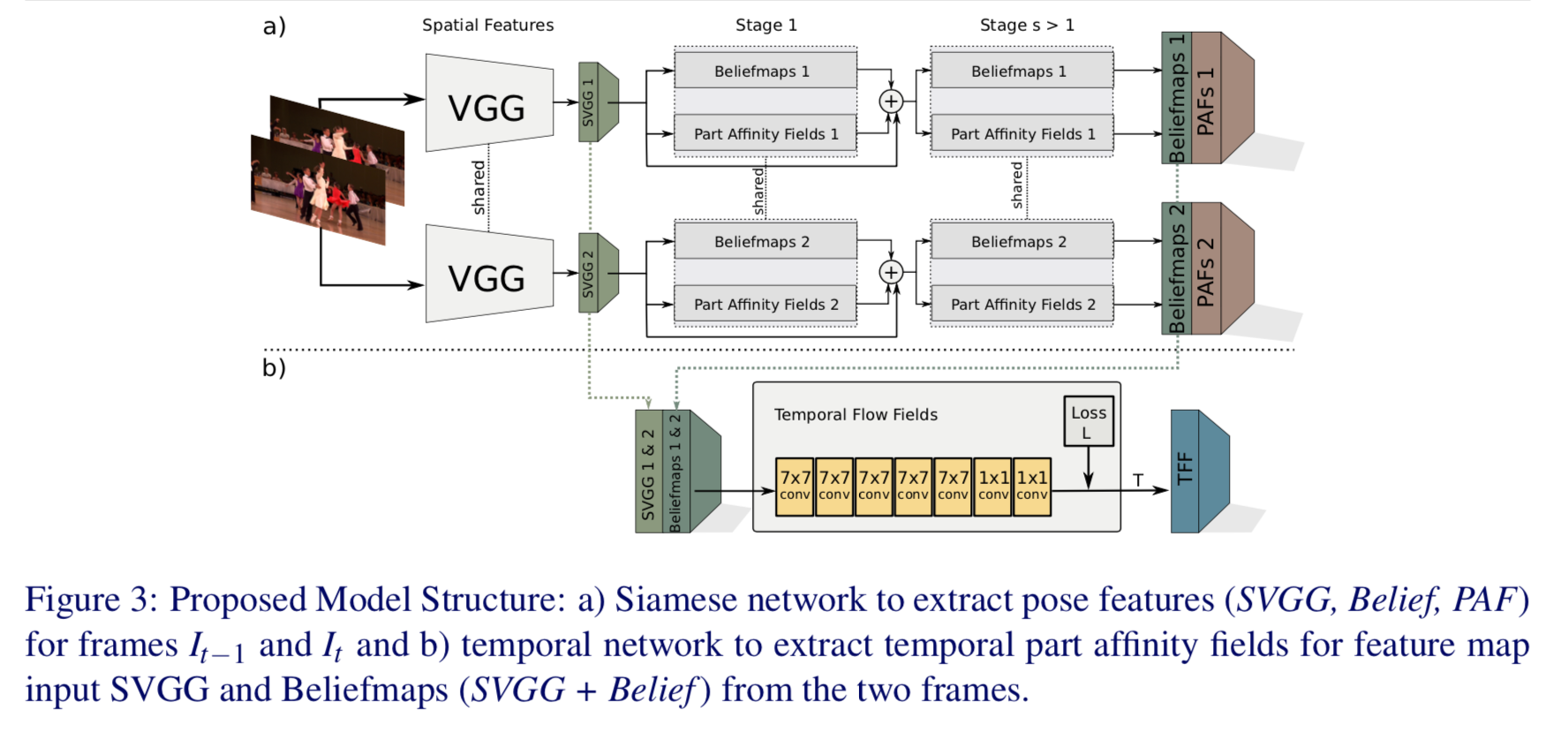
上側(a)部分に関してはほぼOpenPose。
本論文の中核(b)部分では、VGGからの特徴量(SVGG)とheatmapを入力とし、7x7 convで5回、1x1 convで2回畳み込んだ後にTFFを推定する。
loss
(b)部分の loss は以下のようにL2で求める。
\mathcal{L} = \sum^J_{j=1} \sum_{p\in \Omega} M(p) \cdot \| T^{*}_j (p) - T_j(p) \|^2_2
$T^{*}_j (p)$ は ground truthの TFF、$M(p)$ はバイナリーマスクで、アノテーションされてない領域に対して0とする。
推論時の骨格トラッキング
問題設定
求まったTFFなどから骨格形成、およびトラッキングを行うロジックは、以下のように $P_t \in \mathcal{P}_t \ $ と $ \ P'_{t-1} \in \mathcal{P}_{t-1}$ からなる bipartite graph $\mathcal{G}$ に関するエネルギー最大化問題を解くことで達成する。
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\begin{eqnarray}
\hat{z} &=& \argmax_z \sum_{P_t \in \mathcal{P}_t} \sum_{P'_{t-1} \in \mathcal{P}_{t-1}} \Psi_{P_t, P'_{t-1}} \cdot z_{P_t, P'_{t-1}} \\
&s.t.& \forall P_t \in \mathcal{P}_t, \sum_{P'_{t-1} \in \mathcal{P}_{t-1}} z_{P_t,P'_{t-1}} \leq 1 \ and \ \forall P'_{t-1} \in \mathcal{P}_{t-1}, \sum_{P_{t} \in \mathcal{P}_{t}} z_{P_t,P'_{t-1}} \leq 1\\
\end{eqnarray}
ここで $z_{P_t, P'_{t-1}} \in \{ 0,1 \}$ はindicator関数で、$P_t \in \mathcal{P}_t \ $ と $ \ P'_{t-1} \in \mathcal{P}_{t-1}$ とが対応している時に1、他は0となる。
また binary potential $\Psi_{P_t, P'_{t-1}}$ は $P_t$ と $P'_{t-1}$ との類似度を表す。
よって、このエネルギー関数を最大化させることは $P_t$ と $P'_{t-1}$ とが対応している組に関して、その類似度を最大化させること。
ただし、条件から対応する $P_t$ と $P'_{t-1}$ とはそれぞれの点において1つ以下である。
最適化の手法
上記のエネルギー最大化問題を解くため、
Z^t_j = \left\{ z^{p_{t-1},p_t}_j \mid P_t \in \mathcal{P}_t, P_{t-1} \in \mathcal{P}_{t-1} \right\}
なる edge から構成される subgraph $\mathcal{G}_j$ を考える。つまり以下の図のようにフレーム t および t-1 において関節 j と推定された全ての点に関するグラフである。

この組み合わせに関して以下を求める。
E_{aggr}(p^{t-1}_{j,m}, p^t_{j,n}) = \int_{o=0}^{o=1} T_j(i(o))^T \frac{p^t_{j,n} - p^{t-1}_{j,m}}{\| p^t_{j,n} - p^{t-1}_{j,m} \|_2} do,
ここで $i(o) = (1-o)\cdot p^{t-1}_{j,m} + o\cdot p^t_{j,n}$ とする。つまり $p^{t-1}_{j,m} $ から $p^t_{j,n}$ への直線経路。これに沿ってTFFとedgeの単位ベクトルとの内積を線積分するので、TFFが両nodeを対応すると考えているなら1に近い大きな値になるハズ。
ただこれだとTFFに基づいて対応するnodeを求めるため、対象の人の関節位置が動いてないと計算できない。そこで両node間のユークリッド距離 $\Delta p^t_{j,m,n} = \left| p^t_{j,n} - p^{t-1}_{j,m} \right|_2$ を用いて
E_j ( p^{t-1}_{j,m}, p^t]{j,n}) = \begin{cases}
E^T_{aggr} (p^{t-1}_{j,m}, p^t_{j,n}) & if \ \Delta p^t_{j,m,n} \geq \tau_{\Delta} \\
1 & if \ \Delta p^t_{j,m,n} < \tau_{\Delta}
\end{cases}
とする。 $\tau_{\Delta}$ は閾値。
つまり、両nodeの距離が閾値を下回る時は1(対応)とし、上回る時は $E_{aggr}$ を計算する。
こうして骨格 $j$ ごとに求まった $E_j$ の大小で t-1 フレームと t フレームの骨格を対応づけると、t-1 フレームの k さんの右肩と t フレームの m さんの右肩が対応づけられる一方で、t-1 フレームの k さんの左肩と t フレーム目の n さんの左肩が対応づけられるという状況も生じうる。
そこで、PAFにより定まった m さんの骨格、 n さんの骨格を基準として、人ベースでの対応づけとする。
$\Psi_{P^m_{t-1},P^t_{t}}$ を $P^m_{t-1}$ さんと $P^t_{t}$ さんとの全ての骨格の対応づけと考えて、
\Psi_{P^m_{t-1},P^t_{t}} = \sum^J_{j=1} \mathbb{1} (P^{t-1}_{j,m}, P^t_{j,n}) \cdot E_j(P^{t-1}_{j,m}, P^t_{j,n})
とする。ここで indicator関数 $\mathbb{1} (P^{t-1}_{j,m}, P^t_{j,n})$ は両方の関節が検出された場合に1、他を0とする。
そうすると以下の図のように人と人との対応関係ごとに $\Psi_{P^m_{t-1},P^t_{t}}$ が求まるので、この値の大小で正しい対応関係を決めればいい。

実装時のポイント
実装時のポイントは以下
- ベースはOpenPoseのアーキテクチャだが、特徴量抽出部分でVGG19の10層を12層に変更する
- 出力する関節の heat map は閾値 $\tau_{NMS}$ により切り捨てる
- まずOpenPose部分をMicrosoft COCO datasetと PoseTrack datasetの個々の画像で学習させる
- 次にPoseTrack dataset をシーケンシャルに用いてTFF部分を学習させる
- 推論時には4つのスケール(0.5, 1, 1.5, 2)の画像を入力し、その出力を平均して用いる
他の手法との比較
PoseTrack dataset での他の手法との比較結果は以下。

下段 test data で見ると、FlowTrackに次いで2番目のMOTAとなっている。ちなみに現在(19/6/9)ではtopdown方式のPOINetがMOTA=58.41で最もよい。