はじめに
CVPR2019 にacceptされた論文の中から以下の論文
[1] I. Habibie, et. al, "In the Wild Human Pose Estimation Using Explicit 2D Features and Intermediate 3D Representations"
のまとめ
arXivのリンク:
https://arxiv.org/abs/1904.03289
コードは現段階(2019/5/10)では見当たらず
以下ではロジック部分のみまとめ。
概要
- 単眼RGB画像から3次元の骨格を推定するモデル
- スタジオで取得した3次元骨格データとin-the-wildな人の画像にアノテーションしたデータを用いて学習し、in-the-wildな人の画像に対して3次元の骨格を推定する
以下の図は1例。

[1]figure1より
左側のin-the-wildな人の画像に対して、その右の3次元骨格推定値、が2セット。
背景
3次元の骨格データはおおよそ、スタジオでセンサーなどを設置したり、複数のカメラから撮影などをして取得する。
そうやって作成されたデータで学習すると、in-the-wildな人に対する汎化性能が悪い。しかしin-the-wildな人に対して3次元の骨格座標を付与することは困難。
一方でin-the-wildな人に対して2次元の骨格座標を付与することは簡単。
ならばこの2次元のin-the-wildな人の2次元骨格座標とスタジオで撮った3次元骨格座標とを用いてin-the-wildな人の3次元骨格を推定できないだろうか。。。
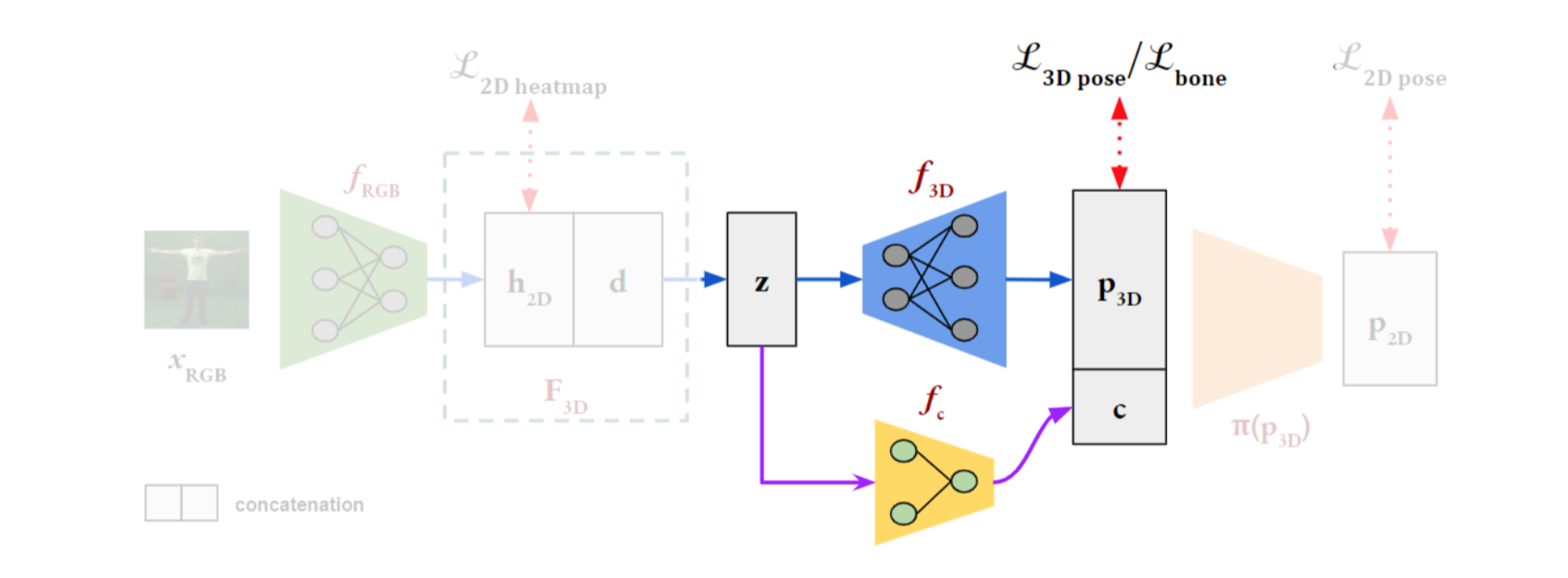
アーキテクチャの概要
全体像は以下。

[1] figure2より
1)左からカラー画像を入力する。
2)$f_{RGB}$ (ResNet-50を使用)で特徴量を抽出し、2次元の関節ヒートマップとその距離を推定する。第1段階の学習では推定した2次元ヒートマップとtargetの2次元ヒートマップとでlossをとる
3)2次元ヒートマップと距離を全結合でlatent $z$ にし、それを2つのneural net $f_{3D}$ と $f_c$ とにわけて入力する。$f_{3D}$ ではルート関節からの各関節の相対座標を求め、$f_c$ ではカメラの内部パラメータを推定する。
4)第2段階の学習では3次元骨格のロス、および各四肢のベクトル同士のロスを計算する。
5)3次元の骨格を2次元にprojectした $P_{2D}$ とtargetの2次元骨格とでロスを計算する。in-the-wildな人の骨格は2次元画像なので、この過程が必要。
アーキテクチャの詳細
カラー画像を入力してheatmapとdepthの推定

カラー画像 ${\rm I} \in \mathbb{R}^{w \times h \times 3} $ を ResNet-50の $f_{RGB}$ に入力する。
出力はヒートマップ ${\rm h}_{2D}$ と depth $\rm d$ 。
{\rm h}_{2D} = \rm (m_1, m_2, \cdots , m_K)
$K$ は関節の個数。一方、ヒートマップのground truthを
{\rm h}^{GT} = ({\rm m}_1^{GT}, {\rm m}_2^{GT}, \cdots , {\rm m}_K^{GT})
とすると、ロスは
\mathcal{L}_{2D} = \sum^K_{k=1} b_k \| {\rm m}_k - {\rm m}_k^{GT} \|^2_2
とL2 normの2乗とする。$b_k \in {0,1}$ は $k$ 番目の骨格が利用可能な場合のみ1。
3次元骨格の推定
まずヒートマップと depth を全結合で1024次元のlatent $z$ にする。
これを2つにわけて、$f_{3D}$ ではルート骨格を起点とした相対3次元骨格 $P_{3D}$ を推定する。
一方 $f_c$ ではカメラの内部パラメータ $c$ を推定する。
まずこの相対3次元骨格同士のロス $\mathcal{L}_{3D\ pose}$ は以下。
\mathcal{L}_{3D\ pose} = \| {\rm P}_{3D} - {\rm P}^{GT} \|^2_2
また各四肢同士のロス $\mathcal{L}_{bone}$ は以下で求める。
\mathcal{L}_{bone} = \sum^K_{k=1} \| \left(Parent ({\rm J}_k ) - {\rm J}_k \right) -\left( Parent ({\rm J}_k^{GT} ) - {\rm J}_k^{GT} \right) \|^2_2
四肢を親関節から股関節へのベクトルで表現している。
なお、in-the-wildな人画像で学習する場合は3次元のground truthがない。この場合は3次元骨格データからランダムにサンプリングされた人の骨格 ${\rm J}_k^{S}$ とのロスのみを計算する。(人の骨格は大体同じという想定か?)
\mathcal{L}_{bone} = \sum^K_{k=1} \| \left(Parent ({\rm J}_k ) - {\rm J}_k \right) -\left( Parent ({\rm J}_k^{S} ) - {\rm J}_k^{S} \right) \|^2_2
3次元骨格を2次元へprojectする

カメラの画像中心を $(c_x , c_y)$ 、焦点距離を $(\alpha_x, \alpha_y)$ として、3次元ワールド座標から2次元画像の座標へ以下で変換する。
\begin{eqnarray}
{\rm \bf p}_{2D} &=& \left[
\begin{array}{ccc}
\pi_x ({\rm \bf p}_{3D}) \\
\pi_y ({\rm \bf p}_{3D})
\end{array}
\right] \\
&=& \left[
\begin{array}{ccc}
\alpha_x {\rm \bf p}_{3D}(x) + c_x \\
\alpha_y {\rm \bf p}_{3D}(y) + c_y
\end{array}
\right]
\end{eqnarray}
この ${\rm \bf p}_{2D}$ とground truthとでロスを計算する。
\mathcal{L}_{2Dpose} = \| {\rm \bf p}_{2D} - {\rm \bf p}_{2D}^{GT} \|^2_2