1. はじめに

バンドル調整の理論を整理した上でnumpyで実装してみる
バンドル調整はレーベンバーグ・マーカンタイル法を用いる
実装で用いるdatasetはOxfordのDinosaur
今回はrotation, translate, カメラ内部行列は既知のものを使い、対象物の３次元座標のみを最適化する

2. 参考文献・図書

レーベンバーグの原論文
1944に発表されたこの手法の最初の論文。Wikipediaによると、その後何人かによって再発見されてるみたい
[1]Levenberg, Kenneth (1944). “A method for the solution of certain non-linear problems in least squares”. Quarterly of Applied Mathematics 2 (2): 164–168
https://www.ams.org/journals/qam/1944-02-02/S0033-569X-1944-10666-0/
- よく使うコンピュータ・ビジョン本の解説（１）
  [2] Simon J. D. Prince. "Computer Vision models, learning, and inference". cambridge.
  16.6.1やAppendix B2.3にGauss-Newton法を使うバンドル調整が記載されてるが、今回の実装とは少し異なる。
よく使うコンピュータ・ビジョン本の解説（２）
[3] Richard Hartley, Andrew Zisserman. "Multiple View Geometry in computer vision". cambridge.
P600のAppendixのA6.2にレーベンバーグ・マーカンタイル法を用いたバンドル調整が記載されているが、Gauss-Newton法の応用例としている。
金谷先生の本（１）
[4]金谷健一著 "３次元回転" 共立出版
勉強会でも使わせてもらった金谷先生の回転本。6.8にレーベンバーグ・マーカンタイル法を用いたバンドル調整が記載されているが、上記の文献と若干異なる。
金谷先生の本（２）
[5] 金谷健一ら "３次元コンピュータビジョン計算ハンドブック" 森北出版
11章にレーベンバーグ・マーカンタイル法を用いたバンドル調整とOxfordのDinosaur datasetを用いた実装例に関して記載されている。
金谷先生系の資料
[6] 岩本祐輝ら "３次元復元のためのバンドル調整の実装と評価" 情報処理学会報告 IPSJ SIG Technical Report
上記[4]と内容はほぼ同じ

今回は[4]、[5]、[6]に沿った内容とする。

3. 用いるdataset

OxfordのMulti-view data
https://www.robots.ox.ac.uk/~vgg/data/mview/
これの一番上のDinosaur。
下図のようにゴジラのおもちゃを1周回転させる間に画像を複数枚撮影している。画像は36枚。（10度ずつある？）

この特徴点に対応する画像上の座標一覧と、36枚の画像に対応するカメラ行列が与えられている。特徴点は全部で4,983点。

4. バンドル調整を超ざっくり整理

4.1 問題設定

M枚の画像、それにわたる特徴点 x が N個与えられた状況を考える
未知数はカメラの内部パラメータ ${\bf K}$、回転 ${\bf R}$、遷移 ${\bf t}$、各特徴点 $\alpha$ の3D world座標 ${\bf w}_\alpha$ とする。
これをレーベンバーグ・マーカンタイル法を用いたバンドル調整で求める

4.2 最適化問題の定式化

特徴点を ${\bf w}$ を画像にprojectして ${\bf x}$ となるとして、この対数尤度を最大化させることを考える。

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\hat{\bf \xi} = \argmax_{\bf \xi} \left[ \sum_{\alpha=1}^N \sum_{\kappa=1}^M \log \left[ Pr({\bf x}_{\alpha, \kappa} | {\bf w}_\alpha, {\bf K}, {\bf R}_{\kappa}, {\bf t}_{\kappa}) \right] \right] \tag{4.2.1}

${\bf \xi}$ は未知のパラメータ全て。

projectした特徴点と実際の画像状の特徴点との誤差が理想的なpinholeモデルに対して正規分布に従うと考えて最小二乗法で解く。

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}

\begin{eqnarray}
\hat{\bf \xi} &=& \argmax_{\bf \xi} \left[ \sum_{\alpha=1}^N \sum_{\kappa=1}^M \log \left[ {\rm Norm}_{{\bf x}_{\alpha, \kappa} } \left[  \left[ {\bf K}{\bf R}_{\kappa}^{\top} ( {\bf I} \ | - {\bf t}_{\kappa}){\bf w}_\alpha \right] ,  \sigma^2 {\bf I} \right]  \right] \right]  \tag{4.2.2} \\


&=& \argmin_{\bf \xi} \left[ \sum_{\alpha=1}^N \sum_{\kappa=1}^M \left[ \left( {\bf x}_{\alpha, \kappa} - {\bf K}{\bf R}_{\kappa}^{\top} ( {\bf I}\  | - {\bf t}_{\kappa}){\bf w}_\alpha \right)^{\top} \left( {\bf x}_{\alpha, \kappa} - {\bf K}{\bf R}_{\kappa}^{\top} ( {\bf I} \ | - {\bf t}_{\kappa}){\bf w}_\alpha \right) \right] \right]  \tag{4.2.3} \\

&=& \argmin_{\bf \xi} E \tag{4.2.4}

\end{eqnarray}

5. レーベンバーグ・マーカント法による解法とその実装例

5.1

ここでカメラ行列な部分をまとめて

\begin{eqnarray}
{\bf K}{\bf R}_{\kappa}^{\top} \left[ {\bf I} \ | - {\bf t}_{\kappa} \right]
 &=& {\bf P}_{\kappa} \\
&=&
\begin{bmatrix}
P^{11} & P^{12} & P^{13} & P^{14}\\
P^{21} & P^{22} & P^{23} & P^{24}\\
P^{31} & P^{32} & P^{33} & P^{34}\\
\end{bmatrix} \tag{5.1.1}
\end{eqnarray}

とするとpinholeモデルの関係は

\begin{eqnarray}
{\bf x} &\simeq& {\bf P}_{\kappa} {\bf w} \\

\begin{bmatrix}
x \\
y \\
1 \\
\end{bmatrix}
 &\simeq&
\begin{bmatrix}
P^{11} & P^{12} & P^{13} & P^{14}\\
P^{21} & P^{22} & P^{23} & P^{24}\\
P^{31} & P^{32} & P^{33} & P^{34}\\
\end{bmatrix}
\begin{bmatrix}
X \\
Y \\
Z \\
1 \\

\end{bmatrix} \tag{5.1.2}
\end{eqnarray}

なのでこれを x と y に関してまとめると

\begin{eqnarray}
x_{\alpha} &=& \frac{P_{\kappa}^{11} X_{\alpha} + P_{\kappa}^{12} Y_{\alpha} + P_{\kappa}^{13} Z_{\alpha} + P_{\kappa}^{14}}{P_{\kappa}^{31} X_{\alpha} + P_{\kappa}^{32} Y_{\alpha} + P_{\kappa}^{33} Z_{\alpha} + P_{\kappa}^{34}}, \tag{5.1.3} \\
&=& \frac{p_{\alpha \kappa}}{r_{\alpha \kappa}}, \tag{5.1.4} \\
\\


y_{\alpha} &=& \frac{P_{\kappa}^{21} X_{\alpha} + P_{\kappa}^{22} Y_{\alpha} + P_{\kappa}^{23} Z_{\alpha} + P_{\kappa}^{24}}{P_{\kappa}^{31} X_{\alpha} + P_{\kappa}^{32} Y_{\alpha} + P_{\kappa}^{33} Z_{\alpha} + P_{\kappa}^{34}}, \tag{5.1.5} \\
&=& \frac{q_{\alpha \kappa}}{r_{\alpha \kappa}}, \tag{5.1.6} \\

\end{eqnarray}

最後の $p_{\alpha \kappa}, q_{\alpha \kappa}, r_{\alpha \kappa}$ は[4]などに従って後の計算のためにまとめた。

この表記で (4.2.3)、(4.2.4) の目的関数 E を書き直すと、

\begin{eqnarray}
E &=&  \sum_{\alpha=1}^N \sum_{\kappa=1}^M I_{\alpha, \kappa} \left[ \left( \frac{p_{\alpha \kappa}}  {r_{\alpha \kappa}} - x_{\alpha, \kappa} \right)^2 + \left( \frac{q_{\alpha \kappa}}  {r_{\alpha \kappa}} - y_{\alpha, \kappa} \right)^2 \right]   \tag{5.1.7} \\

\end{eqnarray}

となる。$I_{\alpha, \kappa}$ は Indicator関数で第 $\alpha$ 点が第 $\kappa$ 画像に写っているときに 1 、そうでないときは 0 とする。

5.2

ニュートン法的な最適化だと、

{\bf \xi}^{t+1} = {\bf \xi}^{t} - \lambda \cdot \left( \nabla_{\bf \xi}^2 E({\bf \xi})  \right)^{-1} \cdot \nabla_{\bf \xi} E({\bf \xi})   \tag{5.2.1} \\

としたいので、目的関数 E を各パラメータ ${\bf \xi}$ で１回微分した値、２回微分した値

\nabla_{\bf \xi}^2 E({\bf \xi}), \nabla_{\bf \xi} E({\bf \xi}) \tag{5.2.2} \\

がほしい。だが、いきなりこれを求めると大変なので、[4], [5], [6]などに従って $p_{\alpha \kappa}, q_{\alpha \kappa}, r_{\alpha \kappa}$ を間にかませる。

(5.1.7)式をパラメータの k 番目で微分すると

\begin{eqnarray}
\frac{\partial E}{\partial {\bf \xi}_k} &=&  \sum_{\alpha=1}^N \sum_{\kappa=1}^M \frac{2}{r_{\alpha \kappa}^2} \left[ 

\left( \frac{p_{\alpha \kappa}}  {r_{\alpha \kappa}} - x_{\alpha, \kappa} \right)

 \left( r_{\alpha \kappa} \frac{\partial p_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} - p_{\alpha \kappa} \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} \right) \right. \\

 &+& \left. \left( \frac{q_{\alpha \kappa}}  {r_{\alpha \kappa}} - y_{\alpha, \kappa} \right)

\left( r_{\alpha \kappa} \frac{\partial q_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} - q_{\alpha \kappa} \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} \right)

  \right]   \tag{5.2.3} \\

\end{eqnarray}

次に２回目を微分するが、ここで反復が進行すると

\begin{eqnarray}
\left( \frac{p_{\alpha \kappa}}  {r_{\alpha \kappa}} - x_{\alpha, \kappa} \right) &\simeq& 0, \\
\left( \frac{q_{\alpha \kappa}}  {r_{\alpha \kappa}} - y_{\alpha, \kappa} \right) &\simeq& 0,\tag{5.2.4} \\

\end{eqnarray}

となるので、その項は削除する。これをガウス・ニュートン近似というらしい。

\begin{eqnarray}
\frac{\partial E}{\partial^2 {\bf \xi}_k {\bf \xi}_l} &=&  \sum_{\alpha=1}^N \sum_{\kappa=1}^M \frac{2}{r_{\alpha \kappa}^4} \left[ 

\left( r_{\alpha \kappa} \frac{\partial p_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} - p_{\alpha \kappa} \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} \right)

 \left( r_{\alpha \kappa} \frac{\partial p_{\alpha \kappa}}  {\partial {\bf \xi}_{l}} - p_{\alpha \kappa} \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}_{l}} \right) \right. \\

 &+& \left. \left( r_{\alpha \kappa} \frac{\partial q_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} - q_{\alpha \kappa} \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}_{k}} \right)

\left( r_{\alpha \kappa} \frac{\partial q_{\alpha \kappa}}  {\partial {\bf \xi}_{l}} - q_{\alpha \kappa} \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}_{l}} \right)

  \right]   \tag{5.2.5} \\

\end{eqnarray}

そうすると、１回微分、２回微分ともに

\frac{\partial p_{\alpha \kappa}}  {\partial {\bf \xi}}, \frac{\partial q_{\alpha \kappa}}  {\partial {\bf \xi}}, \frac{\partial r_{\alpha \kappa}}  {\partial {\bf \xi}} \tag{5.2.6}

のみの関数となる。よって次章では、これらの値を求めることで、目的関数の各パラーメータによる微分値を求める。

6. 各パラメータによる目的関数の微分

式(5.1.1)を各パラメータに分解すると

\begin{eqnarray}
{\bf P}_{\kappa}
&=&
\begin{bmatrix}
P^{11} & P^{12} & P^{13} & P^{14}\\
P^{21} & P^{22} & P^{23} & P^{24}\\
P^{31} & P^{32} & P^{33} & P^{34}\\
\end{bmatrix} \tag{5.1.1} \\


 &=& {\bf K}{\bf R}_{\kappa}^{\top} \left[ {\bf I} \ | - {\bf t}_{\kappa} \right] \\


&=& \begin{bmatrix}
f & 0 & u_0\\
0 & f & v_0\\
0 & 0 & 1\\
\end{bmatrix} 


\begin{bmatrix}
R^{11} & R^{12} & R^{31} & -t_x \\
R^{12} & R^{22} & R^{32} & -t_y \\
R^{13} & R^{23} & R^{33} & -t_z \\
\end{bmatrix} \tag{6.1.1}


\end{eqnarray}

となる。よってパラメータは焦点距離 $f$、光軸点 $u_0, v_0$、回転のパラメータ、並進のパラメータ $t$ となる。これらに各特徴量の 3dワールド座標関を加えたものに関する微分値を求める。

6.1 ３次元ワールド座標に関する微分

$p_{\alpha \kappa}, q_{\alpha \kappa},r_{\alpha \kappa}$ のそれぞれは、各特徴量の３次元点 $(X, Y, Z)$ と $P$ との線形和となっているので、クロネッカーのデルタ $\delta_{\alpha \beta}$ を用いて

\begin{matrix}
\frac{\partial p_{\alpha \kappa}}{\partial X_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{11}, & 
\frac{\partial p_{\alpha \kappa}}{\partial Y_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{12}, & 
\frac{\partial p_{\alpha \kappa}}{\partial Z_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{13}, \\

\frac{\partial q_{\alpha \kappa}}{\partial X_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{21}, & 
\frac{\partial q_{\alpha \kappa}}{\partial Y_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{22}, & 
\frac{\partial q_{\alpha \kappa}}{\partial Z_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{23}, \\

\frac{\partial r_{\alpha \kappa}}{\partial X_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{31}, & 
\frac{\partial r_{\alpha \kappa}}{\partial Y_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{32}, & 
\frac{\partial r_{\alpha \kappa}}{\partial Z_{\beta}}  = \delta_{\alpha \beta} P_\kappa^{33}, \\

\end{matrix} \tag{6.1.2}

となる。

7 レーベンバーグ・マーカート法

7.1 初期値 X を最小二乗法で求める。

def get_initial_3d_points(df_x, df_y, mat):
    XYZs = np.zeros((3, 0), dtype=np.float32)
    for p_idx in range(len(df_x)):
        XYZ = get_initial_3d_point1(df_x, df_y, mat, p_idx)
        XYZs = np.concatenate((XYZs, XYZ), axis=1)
    return XYZs

def get_initial_3d_point1(df_x, df_y, mat, p_idx=0):
    x_se_valid = df_x.loc[p_idx, (df_x.loc[p_idx] != -1)]
    y_se_valid = df_y.loc[p_idx, (df_y.loc[p_idx] != -1)]

    A = []
    b = []
    for t_idx, v_x in x_se_valid.items():
        time = int(t_idx.split('_', 1)[0])
        v_y = y_se_valid['{}_y'.format(time)]
        Pt = mat['P'][0][time]

        A.append([v_x * Pt[2, 0] - Pt[0, 0], v_x * Pt[2, 1] - Pt[0, 1], v_x * Pt[2, 2] - Pt[0, 2]])
        A.append([v_y * Pt[2, 0] - Pt[1, 0], v_y * Pt[2, 1] - Pt[1, 1], v_y * Pt[2, 2] - Pt[1, 2]])

        b.append([- v_x * Pt[2, 3] + Pt[0, 3]])
        b.append([- v_y * Pt[2, 3] + Pt[1, 3]])

    A = np.array(A, dtype=np.float32)
    b = np.array(b, dtype=np.float32)

    XYZ0 = np.linalg.inv(A.T.dot(A)).dot(A.T).dot(b)
    return XYZ0

さらに初期の再投影誤差 E を求める。またc = 0.0001 とする。

def get_loss(XYZs, df_x, df_y, mat, sample_num=10, time_sample=2):
    E = 0.
    for time1, Pt in enumerate(mat['P'][0]):
        x_act = df_x.loc[:, '{}_x'.format(time1)].values
        y_act = df_y.loc[:, '{}_y'.format(time1)].values

        valid_idx = np.where(x_act!=-1)
        x_act = x_act[valid_idx[0]]
        y_act = y_act[valid_idx[0]]

        xyk = Pt.dot(XYZs[:, valid_idx[0]])
        x_projected = xyk[0] / xyk[2]
        y_projected = xyk[1] / xyk[2]
        E += np.sum((x_act - x_projected) ** 2 + (y_act - y_projected) ** 2)
    return E

E = get_loss(XYZs, df_x, df_y, mat, sample_num=sample_num)
print("E: ", E) # E: 51006.08...

7.2 Xに関するEのgradientとヘッセ行列を求める。

def make_gradient_hessian(param_set, p_mat, q_mat, r_mat, x_mat, y_mat, mask):
    """

    :param param_set: list including several dicts
                     ex) [{'type':'X', 'value':(dp_dX, dq_dX, dr_dX)}, {..}, ..]
    :param p_mat: shape:(4983, 36)
    :param q_mat: shape:(4983, 36)
    :param r_mat: shape:(4983, 36)
    :param x_mat: shape:(4983, 36)
    :param y_mat: shape:(4983, 36)
    :return:
    """
    gradient_list = []
    param_order = []

    r_mat = r_mat + 1e-8
    if 'X' in param_set: # calculate dE / dX
        dp_d, dq_d, dr_d = param_set['X']
        dE_dparam = (2 * 1. / (r_mat ** 2) * mask * ((p_mat / r_mat * mask - x_mat) * (r_mat * dp_d - p_mat * dr_d) + (q_mat / r_mat * mask - y_mat)
                                                  * (r_mat * dq_d - q_mat * dr_d))) * mask
        dE_dparam = np.sum(dE_dparam, axis=1) # -> (4983,)
        gradient_list.append(dE_dparam)
        param_order.append('X')
        
    if 'Y' in param_set: # calculate dE / dY
        dp_d, dq_d, dr_d = param_set['Y']
        dE_dparam = (2 * 1. / (r_mat ** 2) * mask * ((p_mat / r_mat * mask - x_mat) * (r_mat * dp_d - p_mat * dr_d) + (q_mat / r_mat * mask - y_mat)
                                                   * (r_mat * dq_d - q_mat * dr_d))) * mask
        dE_dparam = np.sum(dE_dparam, axis=1)  # -> (4983,)
        gradient_list.append(dE_dparam)
        param_order.append('Y')
        
    if 'Z' in param_set: # calculate dE / dZ
        dp_d, dq_d, dr_d = param_set['Z']
        dE_dparam = (2 * 1. / (r_mat ** 2) * mask * ((p_mat / r_mat * mask - x_mat) * (r_mat * dp_d - p_mat * dr_d) + (q_mat / r_mat * mask - y_mat)
                                                     * (r_mat * dq_d - q_mat * dr_d))) * mask
        dE_dparam = np.sum(dE_dparam, axis=1)  # -> (4983,)
        gradient_list.append(dE_dparam)
        param_order.append('Z')
        
        
    gradient_np = np.array(gradient_list, dtype=np.float32).reshape(-1)[:, np.newaxis] # ((4983 x 3, 1)... (dE / dX(4983), dE / dY(4983), dE / dZ(4983)), 1)

    term0 = []  # -> [[4983, 36], [4983, 36], [4983, 36]]
    term1 = []
    term2 = []
    term3 = []
    term4 = []
    for num_c, param_col1 in enumerate(param_order):

        if param_col1 == 'X' or param_col1 == 'Y' or param_col1 == 'Z':
            dp_dk, dq_dk, dr_dk = param_set[param_col1] # (4983, 36), (4983, 36), (4983, 36)
            term0.append(2 * 1. / (r_mat ** 4) * mask) # (4983, 36)
            term1.append((r_mat * dp_dk - p_mat * dr_dk) * mask) # (4983, 36)
            term2.append((r_mat * dp_dk - p_mat * dr_dk) * mask) # (4983, 36)
            term3.append((r_mat * dq_dk - q_mat * dr_dk) * mask) # (4983, 36)
            term4.append((r_mat * dq_dk - q_mat * dr_dk) * mask) # (4983, 36)

        else:
            pass

    term0 = np.array(term0, dtype=np.float32).reshape(r_mat.shape[0]*3, r_mat.shape[1]) # (4983 x 3, 36)
    term1 = np.array(term1, dtype=np.float32).reshape(r_mat.shape[0]*3, r_mat.shape[1]) # (4983 x 3, 36)
    term2 = np.array(term2, dtype=np.float32).reshape(r_mat.shape[0]*3, r_mat.shape[1]) # (4983 x 3, 36)
    term3 = np.array(term3, dtype=np.float32).reshape(r_mat.shape[0]*3, r_mat.shape[1]) # (4983 x 3, 36)
    term4 = np.array(term4, dtype=np.float32).reshape(r_mat.shape[0]*3, r_mat.shape[1]) # (4983 x 3, 36)
    print("term0.shape:{}, term1.shape:{}, term2.shape:{}, term3.shape:{}, term4.shape:{}".format(term0.shape, term1.shape, term2.shape, term3.shape, term4.shape))

    hessian_np = np.zeros((term0.shape[0], term0.shape[0]), dtype=np.float32) # -> (4983 x 3, 4983 x 3)
    term0 = np.transpose(term0) # (4983 x 3, 36) -> (36, 4983 x 3)
    term1 = np.transpose(term1) # (4983 x 3, 36) -> (36, 4983 x 3)
    term2 = np.transpose(term2) # (4983 x 3, 36) -> (36, 4983 x 3)
    term3 = np.transpose(term3) # (4983 x 3, 36) -> (36, 4983 x 3)
    term4 = np.transpose(term4) # (4983 x 3, 36) -> (36, 4983 x 3)

    for num, (term0_1, term1_1, term2_1, term3_1, term4_1) in enumerate(zip(term0, term1, term2, term3, term4)): # (4983 x 3)
        print("now num:{}".format(num))
        term0_1 = np.tile(term0_1[:, np.newaxis], (1, term1_1.shape[0]))  # (4983 x 3, 4983 x 3)
        term1_1 = np.tile(term1_1[:, np.newaxis], (1, term1_1.shape[0]))  # (4983 x 3, 4983 x 3)
        term3_1 = np.tile(term3_1[:, np.newaxis], (1, term3_1.shape[0]))  # (4983 x 3, 4983 x 3)
        term2_1 = np.tile(term2_1[np.newaxis, :], (term2_1.shape[0], 1))  # (4983 x 3, 4983 x 3)
        term4_1 = np.tile(term4_1[np.newaxis, :], (term4_1.shape[0], 1))  # (4983 x 3, 4983 x 3)
        term12 = term1_1 * term2_1
        term34 = term3_1 * term4_1

        hessian_np += term0_1 * (term12 + term34)  # (4983 x 3, 4983 x 3)
    
    print("gradient_np.shape:{}, hessian_np.shape:{}".format(gradient_np.shape, hessian_np.shape))
    return gradient_np, hessian_np


gradient_np, hessian_np = make_gradient_hessian(param_set, p_mat, q_mat, r_mat, x_mat, y_mat, mask)

7.3 連立方程式を解いて X の更新量を求める

以下の連立方程式を解いて X の更新量を求める。

# step 3) solve a system of equations
def solve_a_system_of_equations_from_hessian_gradient(gradient_np, hessian_np_ori, c):
    delta_param = {}
    hessian_np = copy.deepcopy(hessian_np_ori)
    mul = np.ones(hessian_np.shape, dtype=hessian_np.dtype)
    mul += np.eye(hessian_np.shape[0], dtype=hessian_np.dtype) * c
    hessian_np *= mul
    delta_XYZ = - np.linalg.inv(hessian_np).dot(gradient_np)
    delta_param['X'] = delta_XYZ[:len(delta_XYZ)//3, 0]
    delta_param['Y'] = delta_XYZ[len(delta_XYZ)//3:len(delta_XYZ)//3*2, 0]
    delta_param['Z'] = delta_XYZ[-len(delta_XYZ)//3:, 0]

    return delta_param


delta_param = solve_a_system_of_equations_from_hessian_gradient(gradient_np, hessian_np, c=c)

7.4 パラメータを更新する

パラメータ X を更新する。

# step 4) update parameters
def update_params(XYZs, delta_param):
    # TODO ... only applied for XYZs
    XYZs_mod = copy.deepcopy(XYZs)
    if 'X' in delta_param:
        XYZs_mod[0, :] += delta_param['X']
    if 'Y' in delta_param:
        XYZs_mod[1, :] += delta_param['Y']
    if 'Z' in delta_param:
        XYZs_mod[2, :] += delta_param['Z']
    return XYZs_mod

XYZs_tmp = update_params(XYZs, delta_param)

7.5 誤差が小さくなるまで繰り返す

更新したパラメータで再投影誤差 E' を求め、これが元の誤差 E より小さくなっていなければ $c = c \times 10$ として 7.3 からやり直す。

E_mod = copy.deepcopy(E) + 1.
c = 0.0001
    while E_mod > E:

        # step 3) solve a system of equations
        delta_param = solve_a_system_of_equations_from_hessian_gradient(gradient_np, hessian_np, c=c)

        # step 4) update parameters
        XYZs_tmp = update_params(XYZs, delta_param)

        # step 5) calculate Error with modified parameters
        E_mod = get_loss(XYZs_tmp, df_x, df_y, mat, sample_num=sample_num)
        print("E_mod, ", E_mod)

        c *= 10.

7.6 誤差の変化がなくなるまで続ける

7.5による誤差の変化量が $|E' - E| < \delta$ （δは小さい値）と小さくなれば終了する。

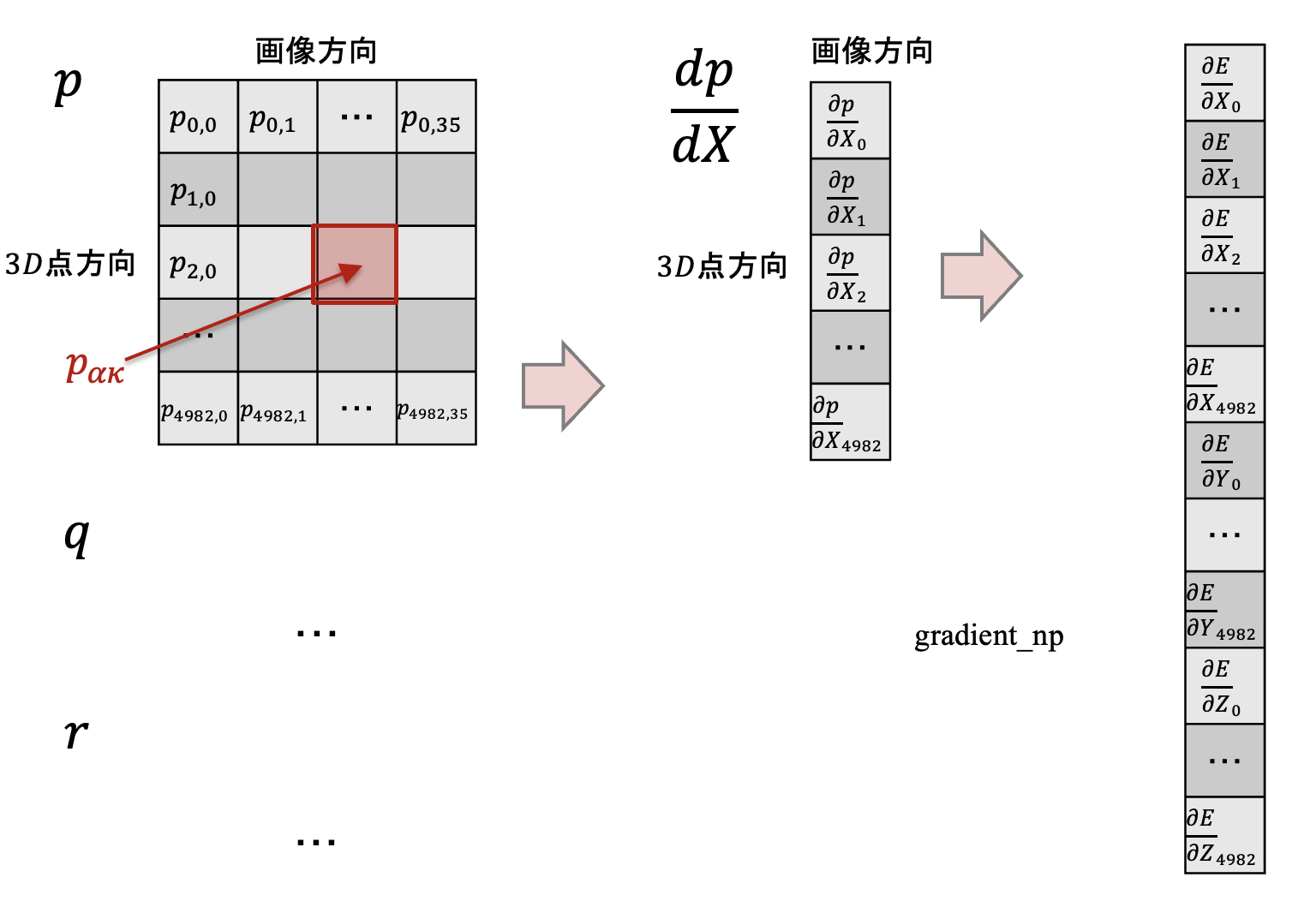
numpy でgradientとヘッセ行列を算出するさいの工夫。

(5.2.3)式、(5.2.5)式を for ループを使わず、numpyの行列計算で一気に演算したい。

そこでgradientは以下のように3D点 X 方向と画像方向に展開した行列を作り、(5.2.3)式のシグマ内を計算した上で画像方向に集計する。

ヘッセ行列を求める(5.2.5)式に関しては以下のように(5.2.5)式の小括弧ごとに3D点X方向、画像方向の２次元配列を作り、それを np.tile() で１軸展開する。その上で(5.2.5)式の大括弧内を計算し、それを画像方向に渡って集計する。

１回のiterationで誤差が 51006.08.. から 51000.82.. になった。

numpyを使ったバンドル調整の実装例