はじめに
ICCV2019 から以下の論文
[1] X. Nie, et. al. "Single-Stage Multi-Person Pose Machines"
http://openaccess.thecvf.com/content_ICCV_2019/papers/Nie_Single-Stage_Multi-Person_Pose_Machines_ICCV_2019_paper.pdf
のまとめ
既にざっくりとした日本語のまとめ記事も存在する。
https://engineer.dena.jp/2019/11/cv-papers-19-2d-human-pose-estimation.html#spm
著者らのコードは見当たらないが、有志のコードはこちらなど
https://github.com/murdockhou/Single-Stage-Multi-person-Pose-Machines
tensorflowで書かれてる。
概要
- 2Dや3Dの姿勢推定をするモデル
- 既存のトップダウン方式やボトムアップ方式は２段階の姿勢推定になるが、本手法（SPR）は骨格の構造まで一気に推定するので１段階で完結する
- 具体的には、人のルートとなる座標、及びそこから各関節への座標の差分を推定する
[1] Figure 1 より一部抜粋
まず上側はトップダウン方式だが、この手法は１）画像から人の矩形を切り取り、２）それに対して骨格を推定する、という２段階。
次に下側のボトムアップ方式だが、この手法は１）画像から各関節の位置等を推定し、２）それを各人に割り当てる、という２段階。
一方で本手法 SPM (Single-Stage Multi-Person Pose Machines) は以下のように
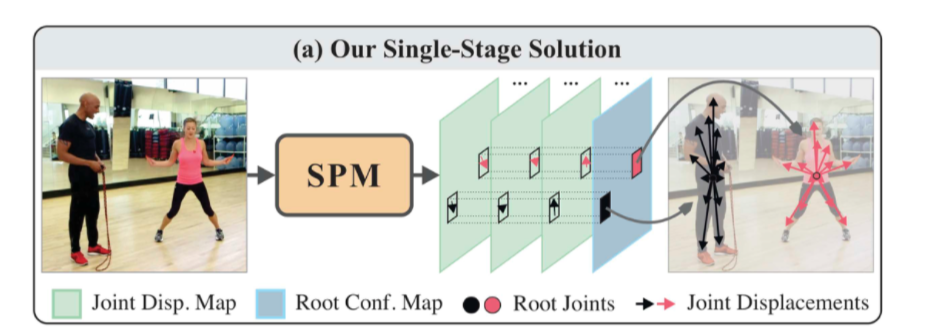[1] Figure 1 より一部抜粋
いきなり骨格構造を出力するので、１段階。
解くべき問題の定式化
まず推定する人の姿勢を $\bar{ \mathcal{P}}$ とすると、
\bar{ \mathcal{P}} = \{ {\bf{P}}^1_i , {\bf{P}}^2_i , \ldots , {\bf{P}}^K_i\}^N_{i=1}
ここで $i$ は画像中の人の ID で、${\bf{P}}^j_i$ は $i$ さんの $k$ 番目の関節の座標。つまり、画像に写ってる全ての人の全ての関節の位置を特定する、ということ。
今回のモデルは 2D 、3D いずれにも対応していて、2D なら ${\bf{P}}^j_i = (x_i^i, y_i^j)$ だし、3D なら ${\bf{P}}^j_i = (x_i^i, y_i^j, z_i^j)$ となる。
既存２手法と本手法の違い
まずトップダウン方式をざっくり定式化すると
\begin{eqnarray}
f &:& I \to \mathcal{B} \\
g &:& \mathcal{B}, I \to \bar{ \mathcal{P}}.
\end{eqnarray}
となる。１段階目 $f$ で画像 $I$ から矩形 $\mathcal{B}$ を推定する。２段階目で 画像 $I$ と矩形 $\mathcal{B}$ から姿勢 $\bar{\mathcal{P}}$ を推定する。
次にボトムアップ方式をざっくり定式化すると
\begin{eqnarray}
g' &:& I \to \mathcal{J, C} \\
f' &:& \mathcal{J, C} \to \bar{ \mathcal{P}}.
\end{eqnarray}
となる。１段階目 $g'$ で画像 $I$ から関節 $\mathcal{J}$ と関節と関節の関連性 $\mathcal{C}$ を推定する。２段階目で関節 $\mathcal{J}$ とその関連性 $\mathcal{C}$ から姿勢 $\bar{\mathcal{P}}$ を推定する。
一方で本手法(Single-stage multi-person pose machine)はいきなり画像 $I$ から 姿勢 $\mathcal{P}$ を推定するので
\begin{eqnarray}
{\rm SPM} &:& I \to \mathcal{P} \\
\end{eqnarray}
である。
SPR (Structured pose representation)
本手法で使う仕組みは後述の Hierarchecal SPRだが、まずはベーシックなSPRから説明。
1) ベーシックな SPR の考え方
ベーシックな SPR (Structured pose representation)は Root Joint とそこからの各関節への変位を求める。
$i$ さんの $j$ 番目の関節は、この人の Root Joint $(x_i^{\rm r}, y_i^{\rm r})$ を用いて
(x_i^j, y_i^j) = (x_i^{\rm r}, y_i^{\rm r}) + (\delta x_i^j, \delta y_i^j)
となる。 $(\delta x_i^j, \delta y_i^j)$ がRoot Jointから各関節への変位。
図にすると、以下のような感じ。
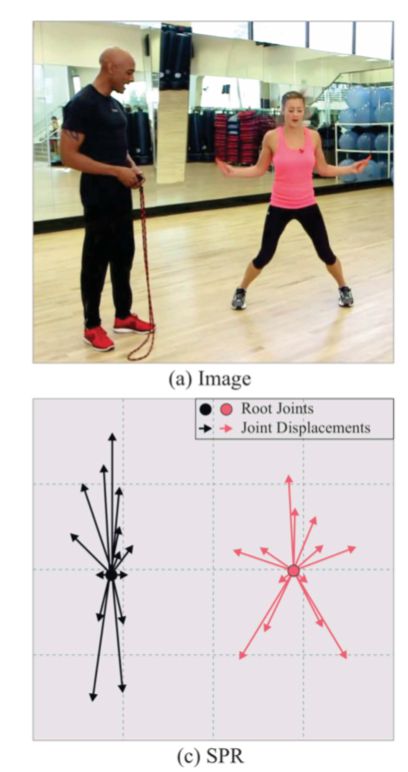[1] Figre 2 より一部抜粋
これを画像中の全ての人、全ての関節に関して求めるので、求める姿勢 $\mathcal{P}$ は
\mathcal{P} = \{ (x_i^{\rm r}, y_i^{\rm r}), (\delta x_i^1, \delta y_i^1) , , (\delta x_i^2, \delta y_i^2), \ldots, (\delta x_i^K, \delta y_i^K) \}^N_{i=1}
となる。
2) Hierarchical SPR
本手法のしくみは SPR を階層構造にした Hierarchical SPR である。
具体的には以下の４層にわける。
（１）１層目で Root Jointを推定する。
（２）２層目で Root Jointから胴体（首・肩・腰）への変位を推定することでこれらの位置を推定する。
（３）３層目で 胴体から頭・肘・膝への変位を推定することでこれらの位置を推定する。
（４）４層目で肘・膝から手首・足首の変位を推定することでこれらの位置を推定する。
図にすると以下の右下。
$l$ 層目の $j$ 関節の位置は $(l-1)$ 層目の $j'$ 関節からの変位とするので、
(x^j_i, y^j_i) = (x^{j'}_i, y^{j'}_i) + (\delta \tilde{x}^{j}_i, \delta \tilde {y}^{j}_i)
となる。例えば、右手首の位置 $(x^j_i, y^j_i)$ は 右肘の位置 $(x^{j'}_i, y^{j'}_i)$ に変位 $ (\delta \tilde{x}^{j}_i, \delta \tilde {y}^{j}_i)$ を足したものとなる。
Root Jointから右肩 -> 右肘 -> 右手首 と足していくと、右手首の位置となる。
(x^j_i, y^j_i) = (x^{\rm r}_i, y^{\rm r}_i) + \sum_{h \in \mathcal{H}^j \backslash \{{\rm r} \}} (\delta \tilde{x}^{h}_i, \delta \tilde {y}^{h}_i)
ここで $\mathcal{H}^j$ は
\mathcal{H}^j = \{ {\rm r }, a^{(1)}, \ldots , a^{(m)} ,j \}
と Root Joint と当該関節、及びその間の関節の集合とするので、$\mathcal{H}^j \backslash { {\rm r } }$ はそこから $\rm r$ を除外した
\mathcal{H}^j = \{a^{(1)}, \ldots , a^{(m)} ,j \}
となる。求める画像中全ての人の全ての関節位置 $\mathcal{P}$ は
\mathcal{P} = \{ (x^{\rm r}_i, y^{\rm r}_i), (\delta \tilde{x}^{1}_i, \delta \tilde {y}^{1}_i), (\delta \tilde{x}^{2}_i, \delta \tilde {y}^{2}_i), \ldots , (\delta \tilde{x}^{K}_i, \delta \tilde {y}^{K}_i) \}^N_{i=1}, given \mathcal{H}
となる。
以下ではベーシックなSPRの方で説明する。
ターゲットの作成方法
1) Root Joint の作成
Root Joint のターゲットは以下のような confidence map で作成する。
画像 $I$ 中の $i$ さんの Root Joint の位置が $(x_i^{\rm r},y_i^{\rm r})$ として、画像中の任意の点 $(x,y)$ のconfidence map ${\rm C}^{\rm r}_i$ は gaussian のexpの部分
{\rm C}^{\rm r}_i (x,y) = \exp \left[ \frac{ - \| (x,y) - (x_i^{\rm r},y_i^{\rm r}) \|^2_2 }{\sigma^2} \right]
で作成する。$\sigma$ は $7$ を用いる。
これを全ての人によって計算し、そのmax値を用いる。
{\rm C}^{\rm r} (x,y) = \max_i {\rm C}^{\rm r}_i (x,y)
2) 各関節に変位におけるターゲット
任意の点 $(x,y)$ における $i$ さんの Root Joint $(x_i^{\rm r},y_i^{\rm r})$ から $i$ さんの $j$ 関節までの変位 ${\rm D}^j_i (x,y)$ は以下。
\begin{eqnarray}
{\rm D}^j_i (x,y) &=&
\begin{cases}
\frac{(\delta x, \delta y)}{Z} & if \ (x,y)\in \mathcal{N}^{\rm r}_i , \\
0 & otherwise
\end{cases} \\
&=&
\begin{cases}
\frac{ \left((x^j_i, y^j_i)-(x,y) \right)}{\sqrt{H^2 + W^2}}
& if \ (x,y)\in \mathcal{N}^{\rm r}_i , \\
0 & otherwise
\end{cases}
\end{eqnarray}
ここで $\mathcal{N}^{\rm r}_i$ は
\mathcal{N}^{\rm r}_i = \left\{ (x,y) \mid \| (x,y) - (x^{\rm r}_i, y^{\rm r}_i) \|^2_2 \leq \tau \right\}
とすることで Root Joint から一定の距離 $\tau$ （今回は７を使用）にある点だけを対象とする。
よって、Root Joint から一定の距離にある点に関して、その点から $j$ 関節へ向けた変位ベクトル $(x^j_i, y^j_i)-(x,y)$ を画像の大きさ $z = \sqrt{H^2 + W^2}$ で正規化したベクトル空間で表現する。
図にするとこんな感じ。
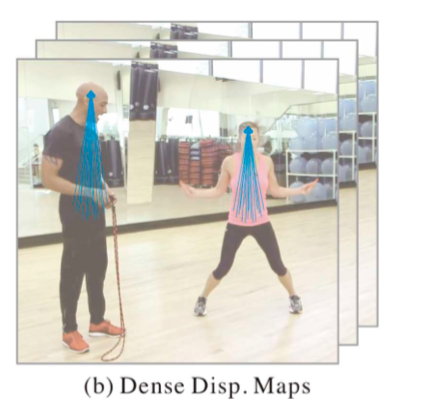
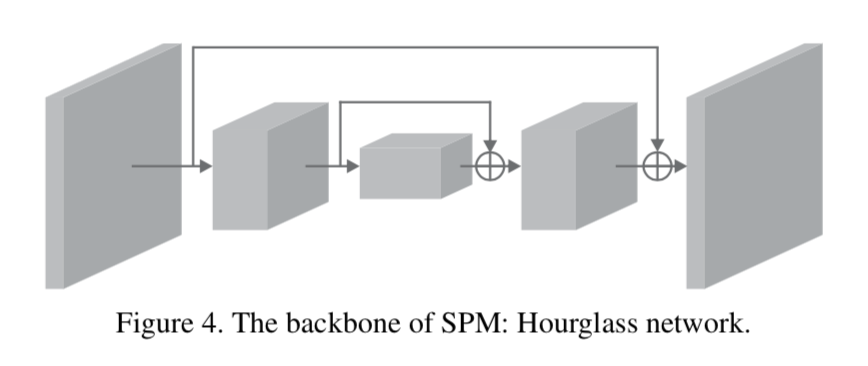
ネットワークのアーキテクチャ
以下の Hourglass module。
loss
Root Joint の confidence map に関するloss $\mathcal{L}^C$ は $\mathcal{l}_2$ 、 各関節の変位は smooth $\mathcal{l}_1$ でも求める。lossの合計 $\mathcal{L}$ は以下。
\mathcal{L} = \sum^T_{t=1} \left(\mathcal{L}^C (\hat{C}^{\rm r}_{(t)}, C^{\rm r}) + \beta \mathcal{L}^D (\hat{D}_{(t)}, D) \right)
$T=8$ は Hourglass モジュールの数。つまり各モジュールからの出力に対して loss を計算して合計する。
ハットの記号はターゲット。$\mathcal{L}^D$ への掛け率 $\beta$ は $0.01$ とする。
推論時の手順
以下の図（[1]Figre1 より一部抜粋）で説明すると
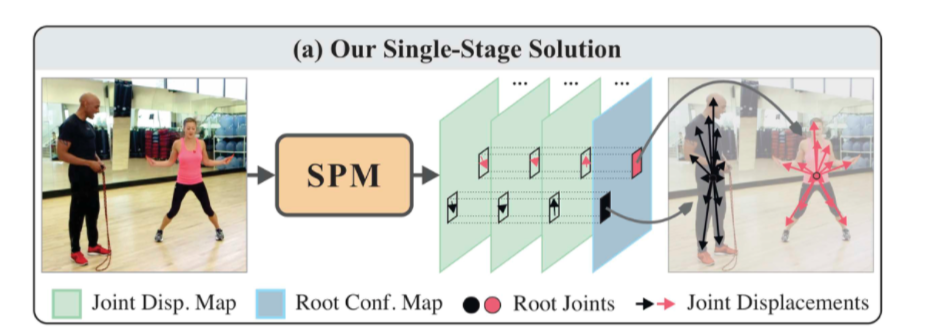
（１）左から画像を入れ、SPMでRoot Joint の confidence map $\hat{{\rm C}}^{\rm r}$ と そこから各関節への変位（Joint Displacement Map) $\hat{{\rm D}}$ を出力する。
（２）non-maximum suppressionで $i$ 人の Root Joints 位置
\left\{ (\hat{x}^{\rm r}_i, \hat{y}^{\rm r}_i ) \right\}^{\hat{N}}_{i=1}
を求める。
（３）$i$ さんの各関節への変位 ${\rm D}^j (x,y)$ は画像のスケールをかけて
Z \cdot D^j (\hat{x}^{\rm r}\_i, \hat{y}^{\rm r}\_i )
で求める。
実験の概要
dataset とメトリクス
2D ヴァージョン
- MPⅡ -> mAP で評価
- MSCOCO -> mAP で評価
- PASCAL-Person-Part -> official AP（これ何？）
3D ヴァージョント
- CMU Panotic -> 3D-PCK@150mm
data augmentation
- 384x384のcrop
- 40度のrotation
- 左右flip
- 拡大縮小
各種設定
- 入力画像は平均0.5, 標準偏差1.0に正規化
- フレームワークはpytorch
- 最適化 RMSprop, learning rate 0.003
MPⅡ dataset の学習結果
他の手法とのmAPの比較
以下が比較結果。
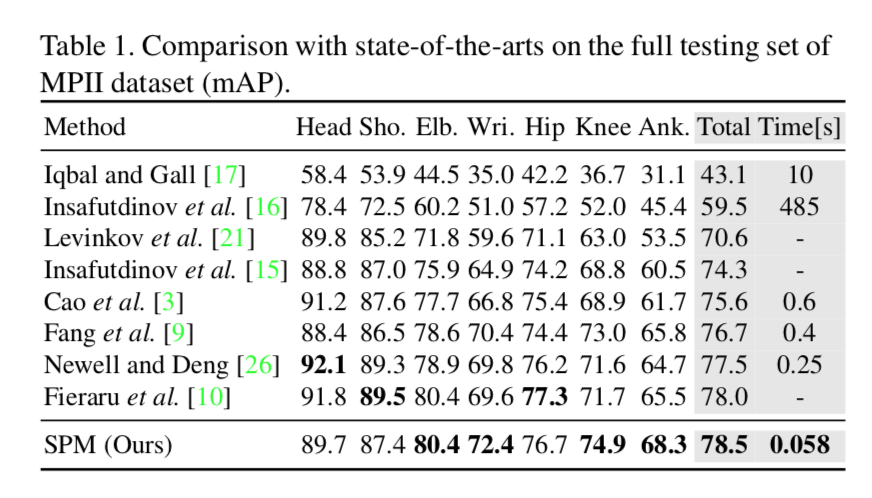
全体的に精度が高い。total の mAPで78.5を達成していて、現段階でのSOTAと主張している。
また推論速度も大きい。OpenPose（表中のCao et al）と比べて１オーダー速い。
OpenPoseは後処理（本著者らのいうところの２段階目）における骨格形成で for loopがあって、そこに時間がかかるが、本手法はニューラルネットで一気に推定するので、早くなるのだろう。
ablation study
ここではベーシックなSPMと hierarchy-SPMを比較している。
hierarcky-SPMの方が若干いい。
定性的評価
[1]Figure 6 より一部抜粋
これら推論結果を見ると、左から３つ目のようなocculusionがあっても、うまく推論している。ただ、Root Joint位置が隠れた場合にどうなるの？という懸念は残る。
その他のdatasetにおける学習結果
PASCAL-Person-Part dataset
PASCAL-Person-Part dataset を用いた場合の定量的評価。
他の手法よりかなりいい。
次に同定性的評価。
右端の画像は、懸念された Root Jointが隠れた場面だが、それなりに推論されてる。隠れた関節の推定はさすがに間違ってるが。。。
MSCOCO datasetを用いた評価
以下が MSCOCO dataset を用いた場合の定量的評価。
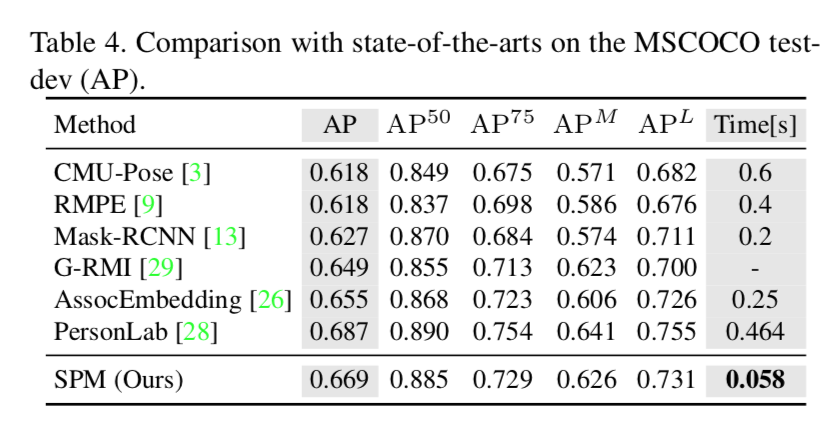
精度では PersonLab に負けてる。off-setのしくみって優秀やね〜。ただ推論速度はさすが。
CMU Panoptic dataset を用いた定性的評価
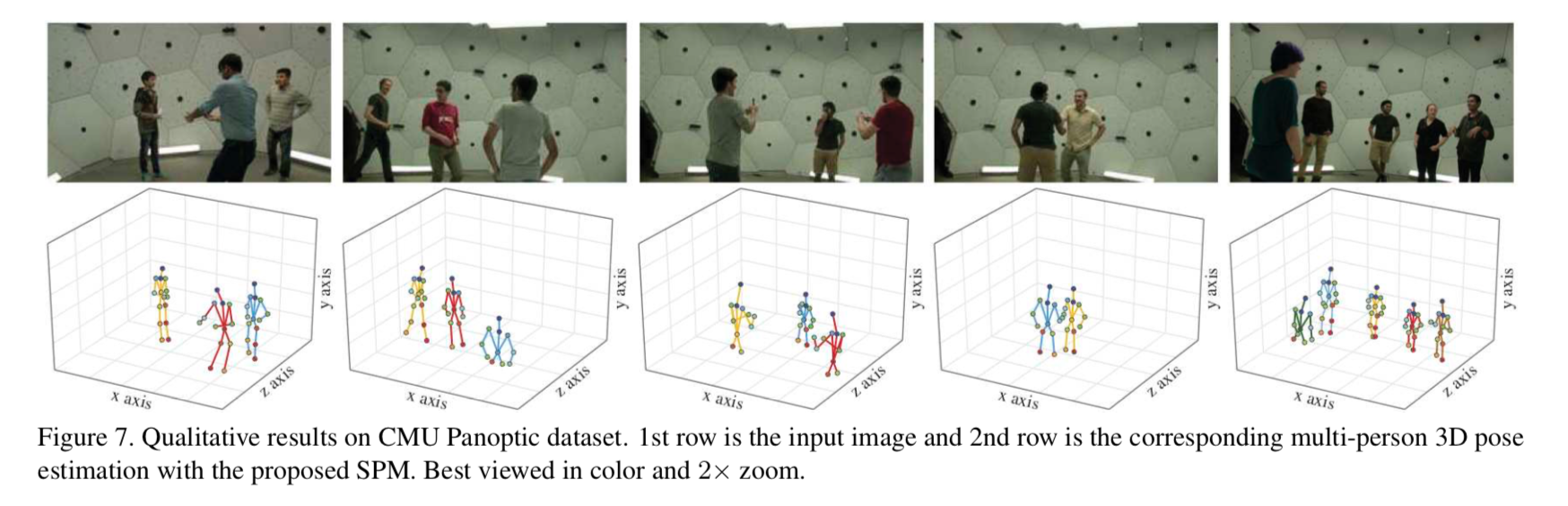
わりと簡単なシーンのみ掲載しているが、ちゃんと推定してるっぽい。
まとめ
- 本モデル SPM (Single-stage multi-person Pose Machine)は世界初の１段階で多人数に対して骨格まで推定するモデルである
- そのしくみ SPR(Structured Pose Representation)は人の特定とその関節位置の特定を統合した手法である
- この手法により、2D および 3D の姿勢推定で高い精度を発揮した