はじめに
MIDL (Medical Imaging with Deep Learning) から以下の論文
[1] H. Kervadec, et. al. "Boundary loss for highly unbalanced segmentation"
のまとめ
arXiv:
https://arxiv.org/abs/1812.07032
著者らのコード:
https://github.com/LIVIAETS/surface-loss
PyTorchで実装されている
概要
- 医療系の画像をsegmentするタスクに関する論文
- back ground と 異常部位の面積に極端なアンバランスがある場合に、lossを工夫することで精度の向上、学習の安定を確保する
- 具体的には、CE や dice loss など領域に基づいた loss とは異なる、境界に基づいた loss を使う
他の class アンバランスなsegmentationに対する学習手法まとめ
class 間で領域に極端なアンバランスがある場合、大体以下のような手法が使われてると思う
- CE を適応的にして focal loss にする
- dice loss のFP, FN を調整して Tversky loss にする
- 上記2つのcombo
- データを均一にして(つまり多い方のデータを少なくして)学習させる
今回の boundary loss はこれらとは違うアプローチ
boundary loss
境界間の距離
本手法の boundary loss は Boykov ら[2] の考え方をもとにしてる。具体的には以下。
まず以下の図のように ground truth の領域を $G$ 、予測したsegmentの領域を $S$ とし、それら領域の境界をそれぞれ $\partial G$ と $\partial S$ とする。
 [1] Figre 2 より抜粋
[1] Figre 2 より抜粋
$p$ を $\partial G$ 上の点、そこから境界に対し垂直な方向に引いた先の $\partial S$ の点を $y_{\partial S} (p)$ とする。
この対応する2点の距離を $\partial G$ に沿って積分したものが求める境界間の距離。
\begin{eqnarray}
{\rm Dist} (\partial G, \partial S) = \int_{\partial G} \| y_{\partial S}(p) - p \|_2^2 dp \tag{1}
\end{eqnarray}
境界から領域への変形
上記の距離だと、推定したsegmentがきれいに別れてない場合(つまりまだらに点在してるような場合)に境界をどう定義するか?など疑問が生じる。
しかし以下のように境界間の距離(の二乗)を境界内領域における距離の和に変形するので大丈夫。
まず以下の図のように $G$ と $S$ との差分領域を $\Delta S$ とし、任意の点 $q$ と ground truth の境界 $\partial G$ 上の点 $p$ のうち $q$ の近傍のものを $z_{\partial G}(q)$ とする。
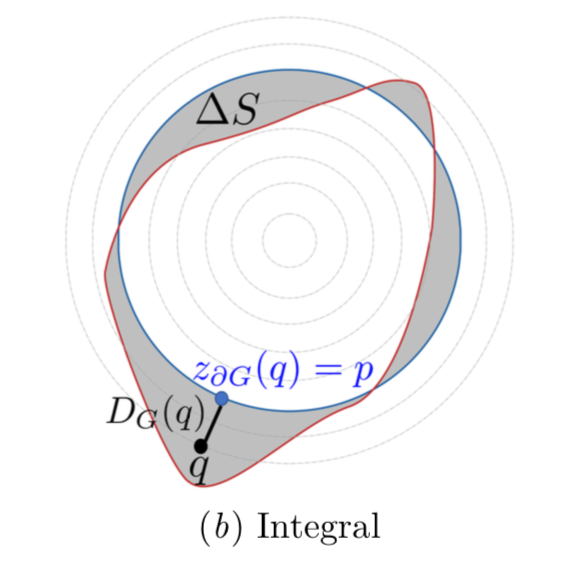
(1)式を以下のように変形するのが目標。
\begin{eqnarray}
{\rm Dist} (\partial G, \partial S) &=& 2 \int_{\Delta S} \| q - z_{\partial G}(q) \|_2 dq \tag{2} \\
&=& 2 \int_{\Delta S} D_G dq \tag{3}
\end{eqnarray}
直感的には $q$ を $z_{\partial G}(q) = p$ から垂直に $y_{\partial S} (p)$ 方向に移動させながら距離 $| q - z_{\partial G}(q) |_2 = D_G$ を積算していくと、なんとなく $\frac{1}{2} | y_{\partial S}(p) - p |_2^2$ になりそうなのはわかる。
つまり $1+2+3+ \cdots +10$ と足していくと、その境界 $10$ を用いて等差数列の和はおおよそ $\frac{1}{2} | 10 - 0 | ^2$ になるようなもの。
実際に計算すると
\int_p^{y_{\partial S}(p)} 2D_G (q) dq
において
\begin{eqnarray}
\frac{d D_G}{d q} &=& \frac{d \| q - z_{\partial G}(q) \|_2}{d q} \\
&=& \frac{1}{2 D_G}
\end{eqnarray}
なので、
\begin{eqnarray}
\int_p^{y_{\partial S}(p)} 2D_G (q) dq &=& \int_0^{\| y_{\partial S}(p) - p \|_2} 2D_G d D_G \tag{4} \\
&=& \| y_{\partial S}(p) - p \|_2^2 \tag{5}
\end{eqnarray}
となる。
よって(1)は
\begin{eqnarray}
{\rm Dist} (\partial G, \partial S) &=& \int_{\partial G} \| y_{\partial S}(p) - p \|_2^2 dp \tag{1} \\
&=& \int_{\partial G} \int_p^{y_{\partial S}(p)} 2D_G (q) dq dp \\
&=& 2 \int_{\Delta S} \| q - z_{\partial G}(q) \|_2 dq \tag{2} \\
\end{eqnarray}
tensorの演算を意識した変形
(3)式(もしくは(2)式)は計算上以下のように変形すると都合がいい
\begin{eqnarray}
\frac{1}{2} {\rm Dist} (\partial G, \partial S) &=& \int_{\Delta S} D_G(q) dq \tag{2}\\
&=& \int_S \phi_G (q) dq - \int_G \phi_G (q) dq \tag{6} \\
&=& \int_{\Omega} \phi_G (q) s(q) dq - \int_{\Omega} \phi_G (q) g(q) dq \tag{7} \\
\end{eqnarray}
ここで
\phi_G (q)= \left\{ \begin{array}{ll}
-D_G(q) & (q \in G) \\
D_G(q) & (otherwise)
\end{array} \right.
つまり、(6)式で差分の $\Delta S$ 領域に関する距離を $S$ における距離と $G$ おける距離との差分に置き換えている。
さらに
s (q)= \left\{ \begin{array}{ll}
1 & (q \in S) \\
0 & (otherwise)
\end{array} \right.
と
g (q)= \left\{ \begin{array}{ll}
1 & (q \in G) \\
0 & (otherwise)
\end{array} \right.
を用いて(7)と表す。$\Omega$ は画像全体。
こうすることで、$\Omega$ に対する演算の multiply となるので、tensorで簡単に計算グラフを作れる。
loss
(7)の2項目は最適化させるパラメータと無関係なので、lossは以下のようになる
\begin{eqnarray}
\mathcal{L}_B (\theta) = \int _{\Omega} \phi_G (q) s_{\theta} (q) dq \tag{8} \\
\end{eqnarray}
これと dice loss(もしくはその応用系)$\mathcal{L}_{GD}$ と組み合わせて、トータルのロスは
\begin{eqnarray}
\mathcal{L}_{total} = \alpha \mathcal{L}_{GD} (\theta) + (1-\alpha) \mathcal{L}_B(\theta) \tag{8} \\
\end{eqnarray}
となる。この掛け率 $\alpha$ は学習の最初は $1.0$ とし(つまり boundary lossの影響をゼロとし)、学習の進行とともに小さくする(boundary loss の影響を大きくする)。
実験と結果
用いたデータセット
- ISLES
- WMH
ベースにしたアーキテクチャ
UNet
メトリクス
- Dice Similarity Coefficient
- Hausdorff Distance
定量的評価
(8)式における $\mathcal{L}_B$ の効果は以下。
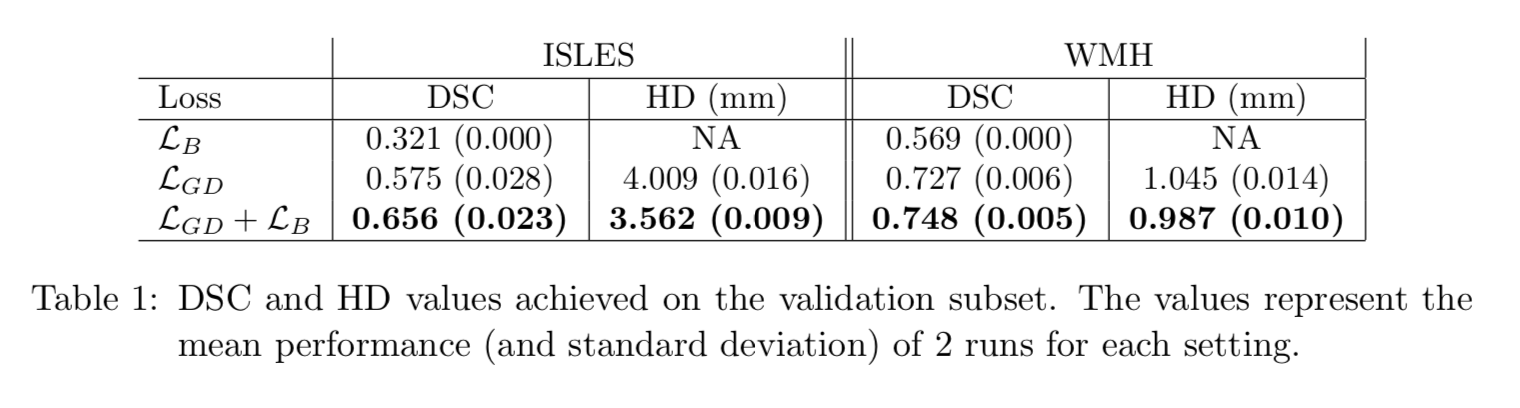
いずれのデータセットにおいても $\mathcal{L}_B$ を加えると精度が上昇している。
また学習時の validation data に対するメトリクスの変化は以下。
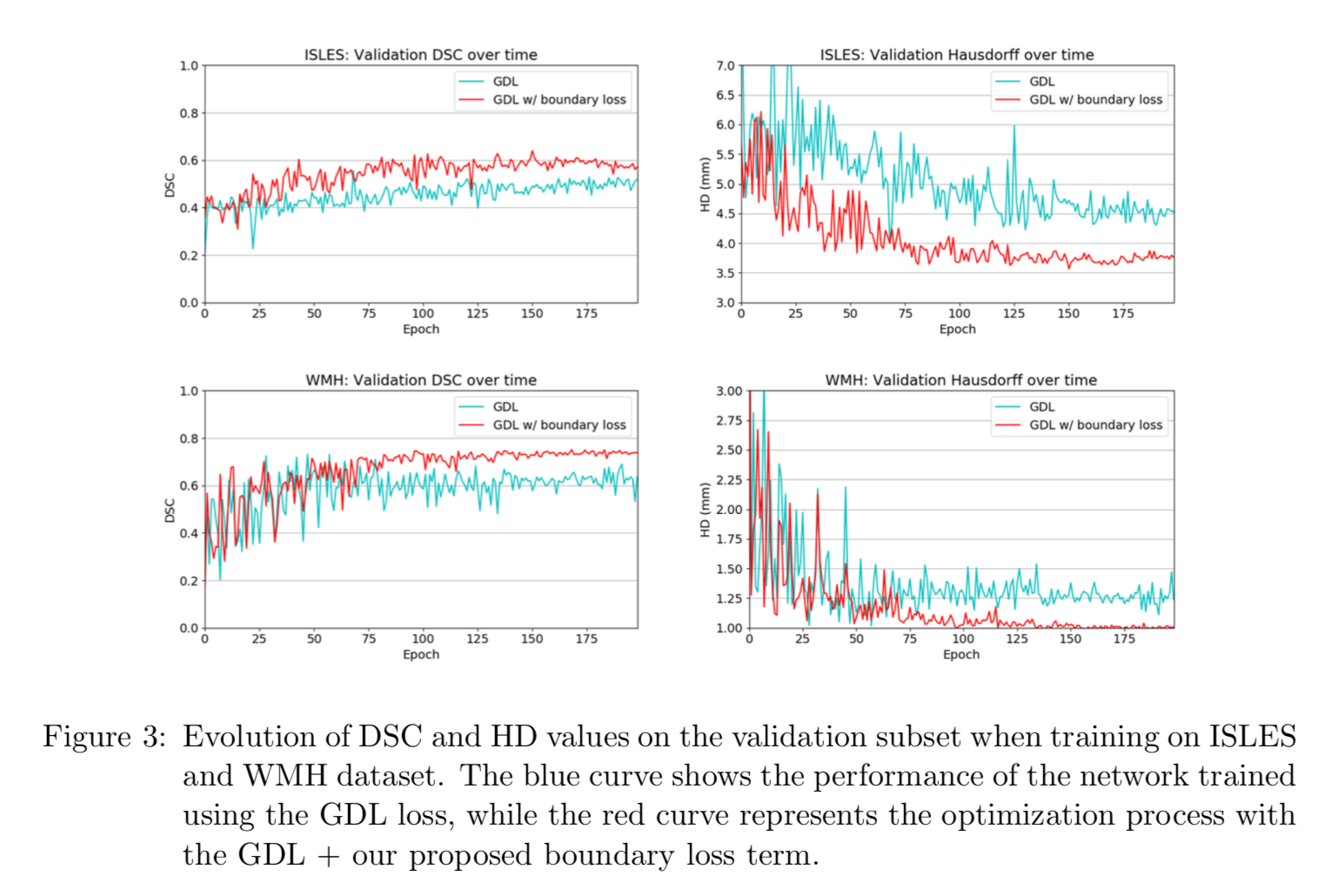
いずれのデータセットにおけるいずれのメトリクスにおいても安定性が増している。
定性的評価
セグメントの結果は以下。
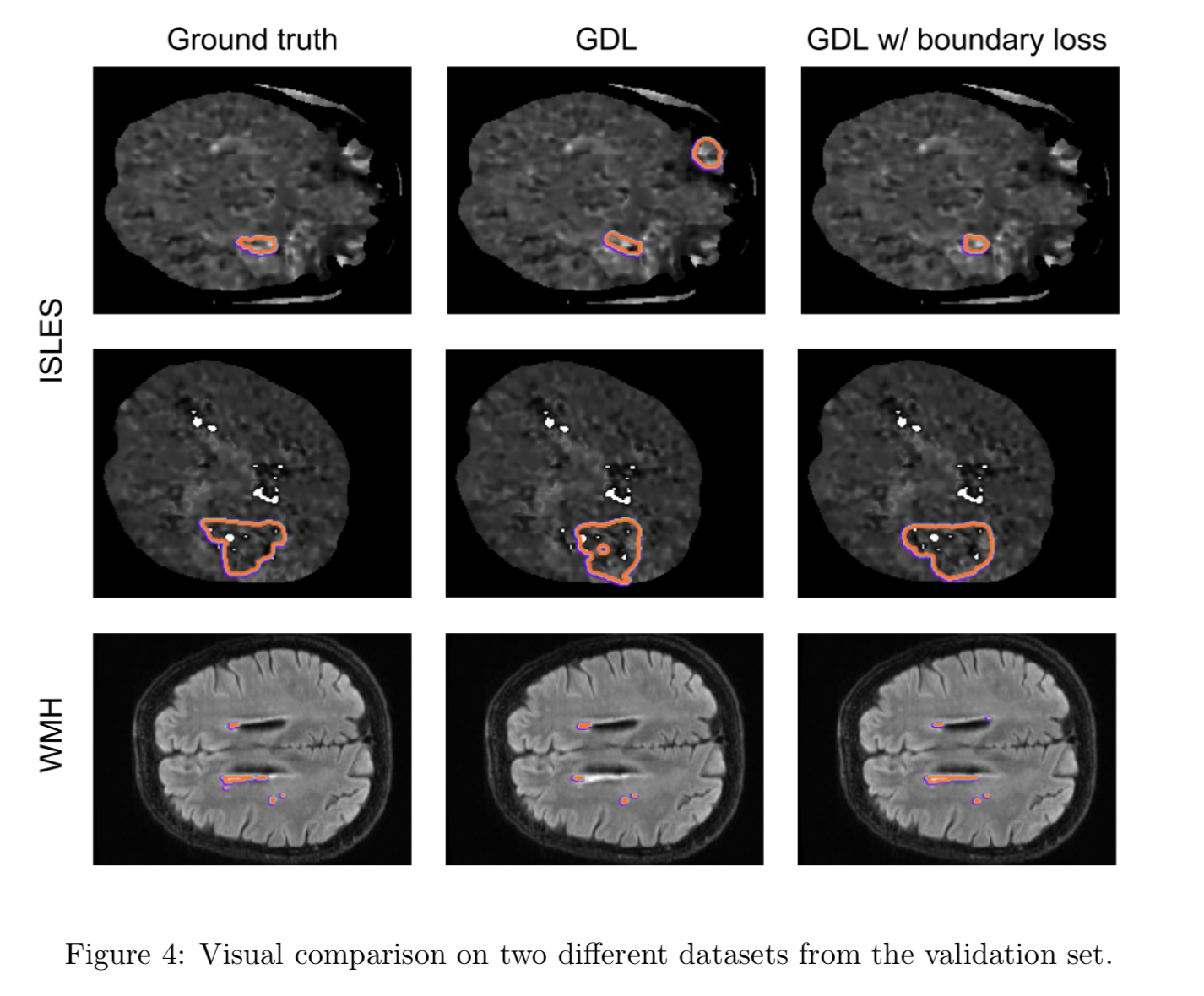
この図を見る限り $\mathcal{L}_B$ を加えるとより正確にセグメントできている。(いいとこどりした可能性はあるが。。。)
結論
class 間で unbalance なタスクに boudary loss を使うと
- 精度が増す
- 学習の安定性が増す
reference
[2] Yuri Boykov, Vladimir Kolmogorov, Daniel Cremers, and Andrew Delong. An integral solution to surface evolution PDEs via geo-cuts. In European Conference on Computer Vision, pages 409–422. Springer, 2006.