はじめに
NIPS2018にacceptされてる論文の中からこちらの論文
S. Kohl, et. al. "A Probabilistic U-Net for Segmentation of Ambiguous Images"をまとめてみた。
NIPS2018の該当ページ
https://nips.cc/Conferences/2018/Schedule?showEvent=11671
arXivには6月から上がってたみたい。
https://arxiv.org/abs/1806.05034
既にarXivTimesにまとめ記事が出てた。
https://github.com/arXivTimes/arXivTimes/issues/797
概要
- VAEとU-Netを組み合わせたアーキテクチャ
- 従来のセグメンテーションモデルと違い、pixel毎に単一のクラスを出力するのではなく、複数の候補を出力する
背景
セグメンテーション・タスクではピクセルごとに何の物体かを予測する。しかし、それだと不都合な場合がある。
例えば室内の画像において、ソファーの下に毛の一部が見えたとしても、それが犬なのか猫なのかわかりにくい。それでも従来のアルゴリズムは無理やり犬だと推定する。
あるいはCT画像で癌っぽいものがあった時に、各ピクセルにおいてとりあえず癌か否かを判断するだろう。しかしそれが間違いであれば問題だ。
代わりに癌である、ない、単なるデキモノ、など複数の予測画像があれば、医者の診断には有効だ。更なる精密検査を行うことによって癌の有無を特定すればいいだろう。
本モデルではこのような複数の候補を出力する。
ネットワークのアーキテクチャ
ネットワークのアーキテクチャは論文中のFigure 1がわかりやすい。
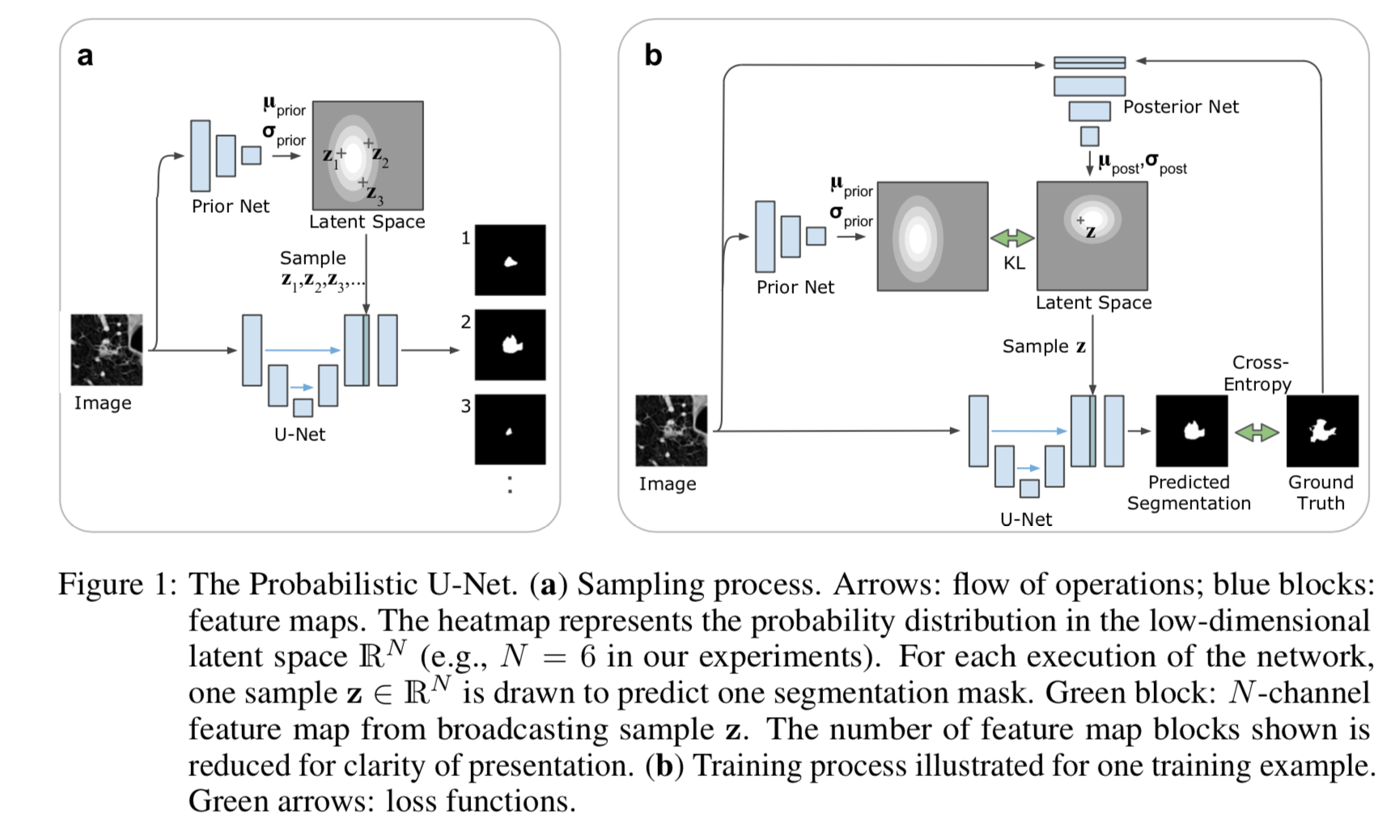
推論時
Figure 1 のaが推論時。下側がUNet構造、上側がVAEのencoderになっている。
まず左から画像XをUNetとencoder両方に入力する。
encoderからはN次元gaussianの事前分布 $\mu_{prior}(X;\omega ) \in \mathbb{R}^N $ と $\sigma_{prior}(X;\omega ) \in \mathbb{R}^N $ を出力する。
この分布から $z_i$ をサンプリングする。
z_i \sim P(\cdot | X) = \mathcal{N}(\mu_{prior}(X;\omega ), diag(\sigma_{prior}(X;\omega )))
これをブロードキャストしてNチャンネルの特徴量とし、UNetにconcatenateして挿入する。
これをさらにconvし、出力 $S_i$ を得る。
S_i = f_{comb.} (f_{U-Net} (X;\theta,z_i;\psi)))
サンプルがm個の場合は、この計算をm回繰り返す。
学習時
学習時はFigure 1 の b。
推論時と比較して、上側のposterior Netとその分布、右側のtargetなどが加わっている。
posterior Netでは入力画像X、そのtarget Yを入力し、事後確率の $\mu_{post}(X, Y;\nu ) \in \mathbb{R}^N $ と $\sigma_{post}(X,Y;\nu ) \in \mathbb{R}^N $ を出力する。
この分布からzをサンプリングする。
z \sim P(\cdot | X,Y) = \mathcal{N}(\mu_{post}(X,Y;\nu ), diag(\sigma_{post}(X,Y;\nu )))
これをUNetに挿入する。
目的関数
lossは2つの要素からなる。
1つ目はUNetの出力とtargetとの交差エントロピー。
2つ目はzの潜在空間に関してpriorとposteriorとでKL divergenceをとる。
\mathcal{L}(Y,X) = \mathbb{E}_{z \sim Q(\cdot | Y,X)} \left[ - \log P_c (Y|S(X,z))) \right] + \beta \cdot KL \left( Q(z|Y,X) \parallel P(z|X) \right)
ここで $KL (Q(z|Y,X) \parallel P(z|X))$ はおそらく
KL (Q(z|Y,X) \parallel P(z|X)) = \frac{1}{2} \left[ \log \frac{|\Sigma_P|}{|\Sigma_Q|} -d + Tr(\Sigma^{-1}_P \Sigma_Q ) + (\mu_P - \mu_Q )^T \Sigma^{-1}_P (\mu_P - \mu_Q ) \right]
かな?(間違ってたら教えてください)
評価
まずメトリクスを定義して、それを用いて類似する他のモデルと比較することで評価する。
1 メトリクス
まず targetも複数候補とする。その上で $d(x,y) = 1 - (IoU)$ として、[2]などに記載されている以下の式で評価する。
D^2_{GED} (P_{gt}, P_{out}) = 2 \mathbb{E} \left[ d \left( S,Y \right) \right] - \mathbb{E} \left[ d \left( S,S' \right) \right] - \mathbb{E} \left[ d \left( Y,Y' \right) \right]
YとY'はtargetからの独立したサンプル、SとS'は予測したセグメンテーションマスクからの独立したsample。
直感的に考えると、まず
\begin{eqnarray}
d(x,y) &=& 1 - (IoU) \\
&=& 1 - \frac{tp}{tp + fn + fp} \\
&=& \frac{fn + fp}{tp + fn + fp}
\end{eqnarray}
なので、これは両者の違いの割合的なもの。
そうすると $D^2_{GED} (P_{gt}, P_{out})$ の1項目 $2 \mathbb{E} \left[ d \left( S,Y \right) \right] $ は予測値とtargetとの違いの割合。
ただ、予測値もtargetも分布に従ってて幅があるので、その分 $ \mathbb{E} \left[ d \left( S,S' \right) \right]$ と $\mathbb{E} \left[ d \left( Y,Y' \right) \right]$ を引く。
そうすると純粋に予測値とtargetとの違いの割合だけが残りそう。
比較対象のモデル
比較対象となるモデルは本モデルと同様に複数の候補を出力する必要がある。
具体的には以下の4つのモデル。

左から。a は赤い部分が dropout 層。Test時にもdropoutすることで複数候補出力できる。
b はモデル自体を複数作るケース。アーキテクチャも学習方法も乱数のシードも同じなら出力は同じとなるだろうが・・・・シードを変えるのだろうか??
c は出力層を複数にするパターン。
d は正規分布からランダムにサンプリングした値をモデルに組み込むパターン。
用いたデータセット
用いたデータセットは以下の2種類
Lung abnormalities segmentation
肺の異常検知用デーセット。
こちらは元々1つの画像に対して4種類のアノーテーションがあるらしく、今回のタスクに向いている。
CityScapes dataset
お馴染みCityScapes。
こちらは1つの画像に1つのアノーテーションしかないので、人工的に複数生み出した。
具体的には「人クラス」に対して「人2クラス」などを新たに作り、「人クラス」の領域を確率的に「人2クラス」する、などとした。
実験の結果
出力画像の比較
本モデル、及び比較対象のモデルから出力された画像は以下。

左側の肺以上検知に関しても、右側のCityScapesに関しても本モデルが一番多様性ありそう。
メトリクスの比較
$D^2_{GED} (P_{gt}, P_{out})$ 値の比較は以下。
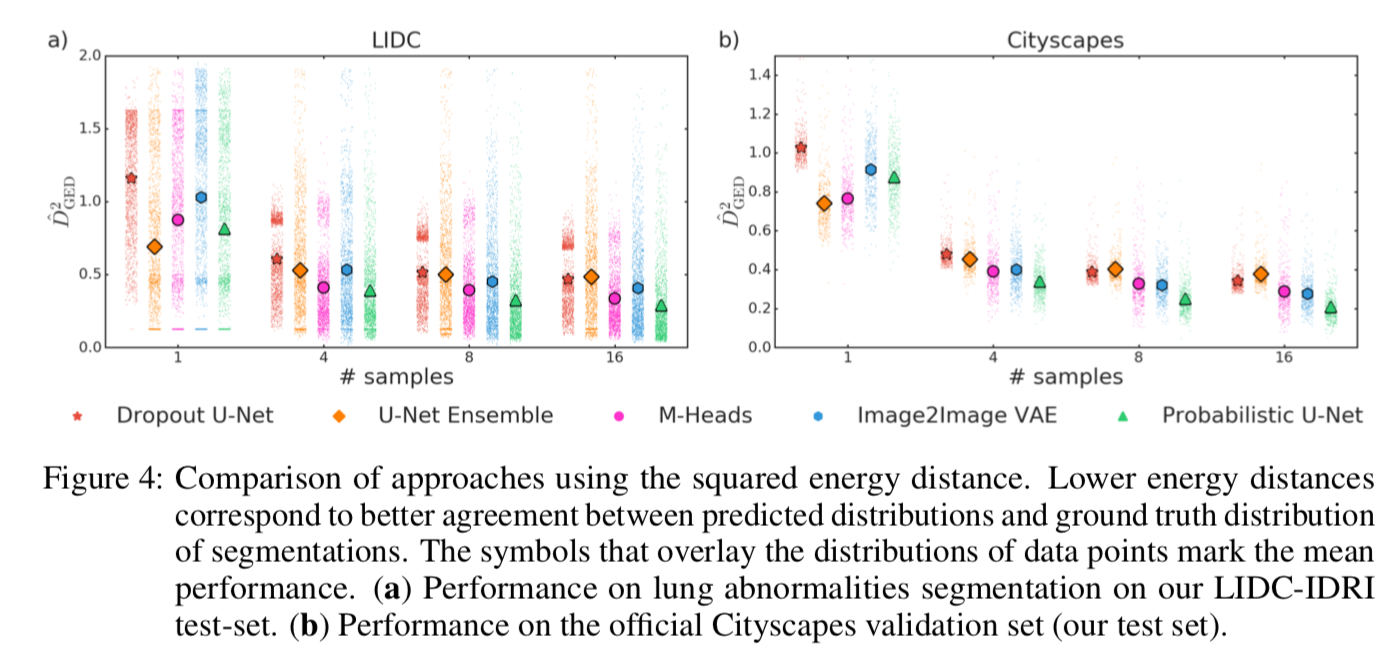
概ね本モデルがいい値出してる。
my サンプルコード
まだ作りかけですが、コードはこちらにupしてます。
https://github.com/masataka46/probabilistic_UNet
my 学習結果
上記のコードを使ってCityScapesで500回くらい学習させた後にtest dataで推論させた結果が以下の画像。(ただし、論文にあるようなアノーテーションの水増しはやってない)
上から元画像、アノーテーション、推論値。
またこのコードの特徴である同じ入力値に対する多様な出力画像は以下。これも500epoch程度学習させた後のtest dataに対するもの。
あまり変化がないね〜。やはりアノーテーションの水増しをやってないので多様性が生まれてないってことかな〜。
reference
[2] T. Salimans, et. al. "Improving GANs using optimal transport"

