はじめに
CVPR2021より以下の論文
[1] A. Pumarola, et. al. D-NeRF: Neural Radiance Fields for Dynamic Scenes. CVPR2021
のまとめ
-
CVF open access
https://openaccess.thecvf.com/content/CVPR2021/html/Pumarola_D-NeRF_Neural_Radiance_Fields_for_Dynamic_Scenes_CVPR_2021_paper.html -
github
https://github.com/albertpumarola/D-NeRF
ライセンス不明
概要
- NeRF系で deformable な物体に対応した先駆け的な論文の1つ
- 3Dの正解データを必要としない
- 単眼カメラで撮影した動画を用いる(NeRFは同時に多方面から撮影)
- fieldを動きの変化を捉えるものとカラーや密度を推定するものの2つにわける
problem formulation
目標
${\rm \bf x} = (x, y, z)$: 物体に関する3次元座標
${\rm \bf c} = (r, g, b)$: 推定するカラー
$\sigma$: 推定する密度
${\rm \bf d} = (\theta,\phi)$: view direction
としたときに目標は
\mathcal{M} :({\rm \bf x}, {\rm \bf d}, t) \rightarrow ({\rm \bf c}, \sigma)
と写像する $\mathcal{M}$ を求めること。NeRF原論文との違いで言うと、物体が動くので時間の要素 t が加わっている。
この $\mathcal{M}$ を直接求めようとする手法もあるが、筆者らの実験では以下のように2段階に分けた方が上手くいくとのこと。
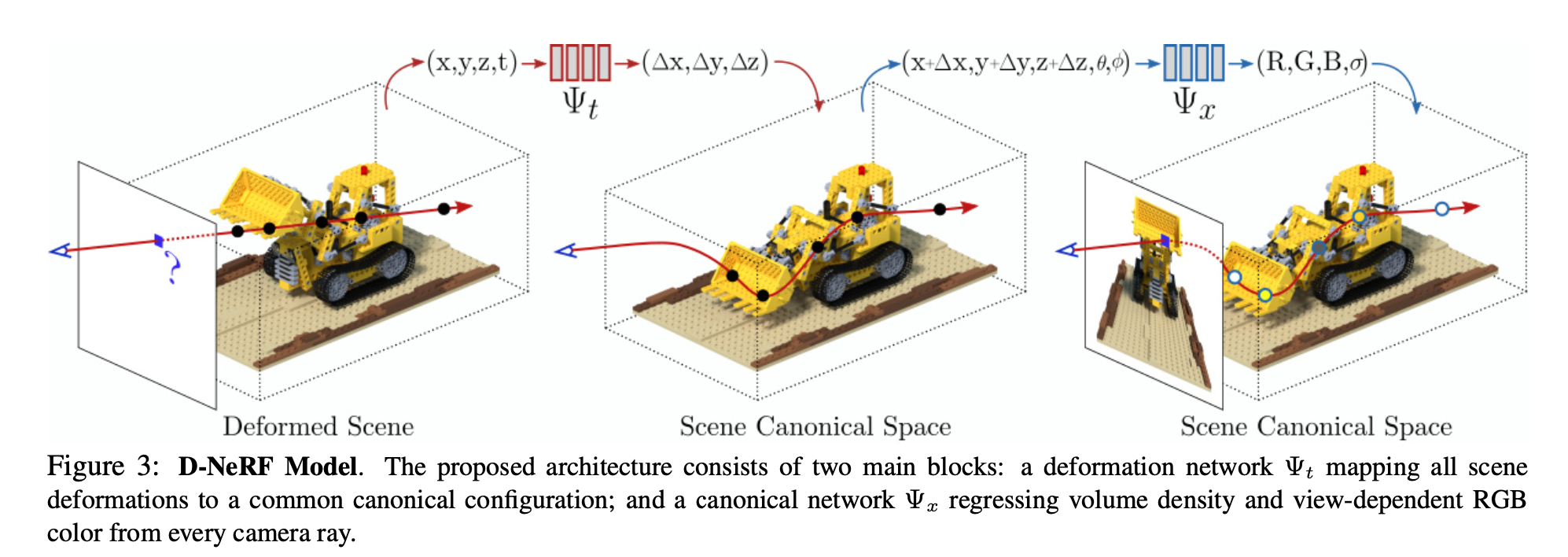
- 与えられたシーン(deformed scene)からcanonicalなシーン(scene canonical space)へ変換する $\Psi_t$
- 与えられたシーン(deformed scene)からcanonicalなシーン(scene canonical space)へ変換する $\Psi_x$
この図にあるように $\Psi_t : ({\rm \bf x}, t) \rightarrow \Delta {\rm \bf x}$ と default の状態(t = 0の状態)に対する差分を出力する。
こうして求まった scene canonical space に対して $\Psi_x : ({\rm \bf x} + \Delta {\rm \bf x}, {\rm \bf d}) \rightarrow ({\rm \bf c}, \sigma)$ で色と密度を推定する。
入力として使うデータ
- ${\rm \bf I}_t \in \mathbb{R}^{H \times W \times 3}$: t 時の画像
- ${\rm \bf T}_t \in \mathbb{R}^{4 \times4} \ {\rm SE}(3)$: t 時のカメラの外部パラメータ
ネットワークのアーキテクチャ
canonical network
8層のMLP。NeRFのネットワークと違い、密度 $\sigma$ も最終層から出力される。
deformation network
こちらも8層のMLP。
canonical network 、あるいは NeRF のMLPと同様、neural networkが高周波なものを再現しにくいという性質を補完するため、入力で以下のように座標 x や向き d encode する。
\gamma (p) = <(\sin {\left( 2^l \pi p \right)}, \cos{\left( 2^l \pi p \right) } >_0^L
volume rendering
canonical space上ではNeRFの neural radiance fieldと同様にレンダリング。
loss
NeRFと同様レンダリングしたカラーと正解値のカラーとの差。
学習に関して
- 収束しやすいようにするため、初めは動画の最初の方の frame のみで学習し、徐々に後半の frame も加えていった
- 画像サイズは 400 x 400
- iterationは800K
- バッチサイズha4096 rays
- 各光線において64点のサンプリング
- 最適化:adam
- 学習時間は Nvidia GTX1080 使って2日かかった
定性的評価
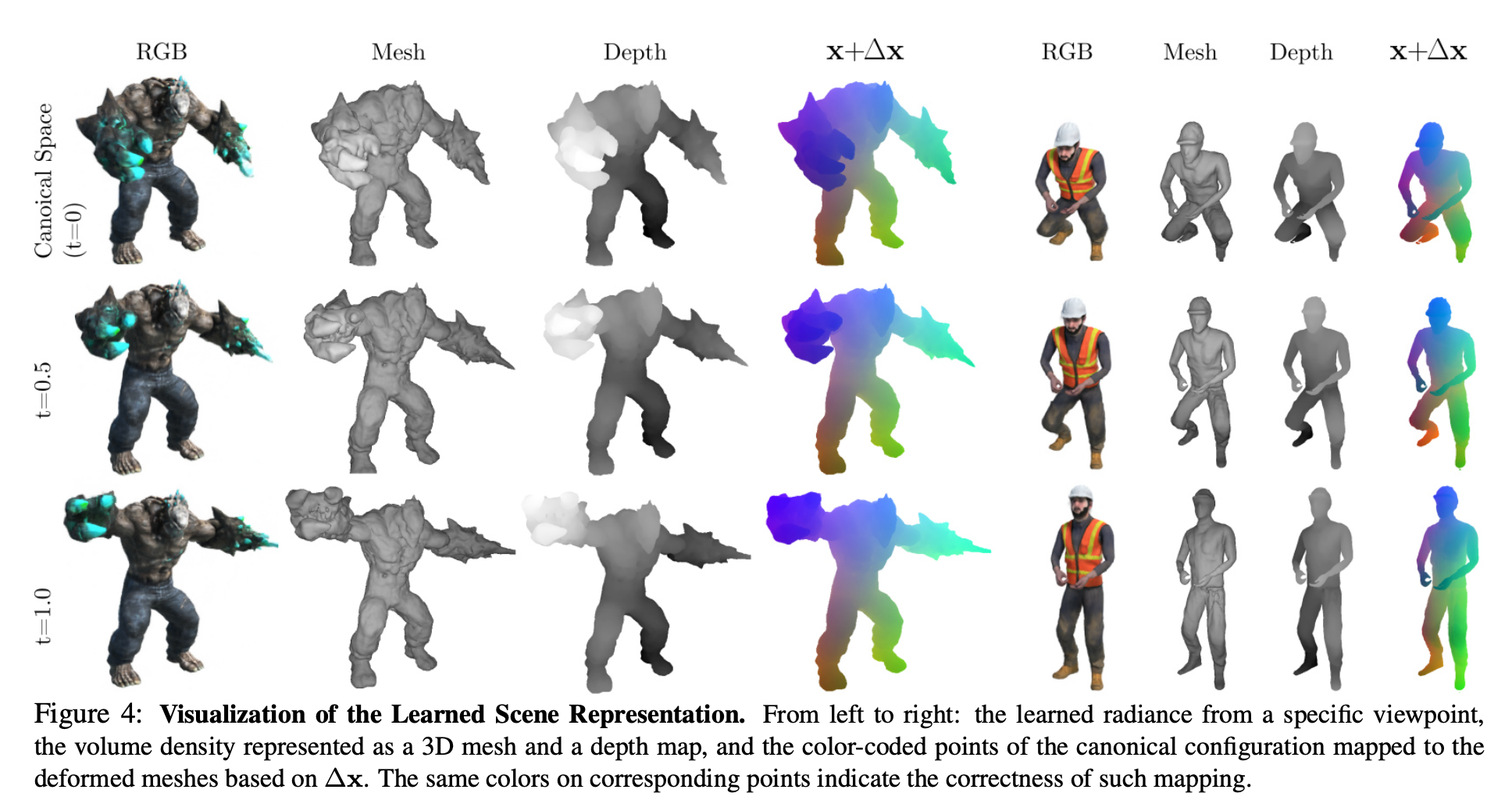
以下の図は学習後の新たな視点に対する推論結果。
各行は上からcanonical space(t=0), t=0.5, t=1.0。
各列は左からカラーをレンダリングしたもの、それを voxcel化してmarching cube algorithでmesh化したもの、depth、canonical spaceに対する変位を可視化するため同じ部位を同じ色としたもの。
定量的評価
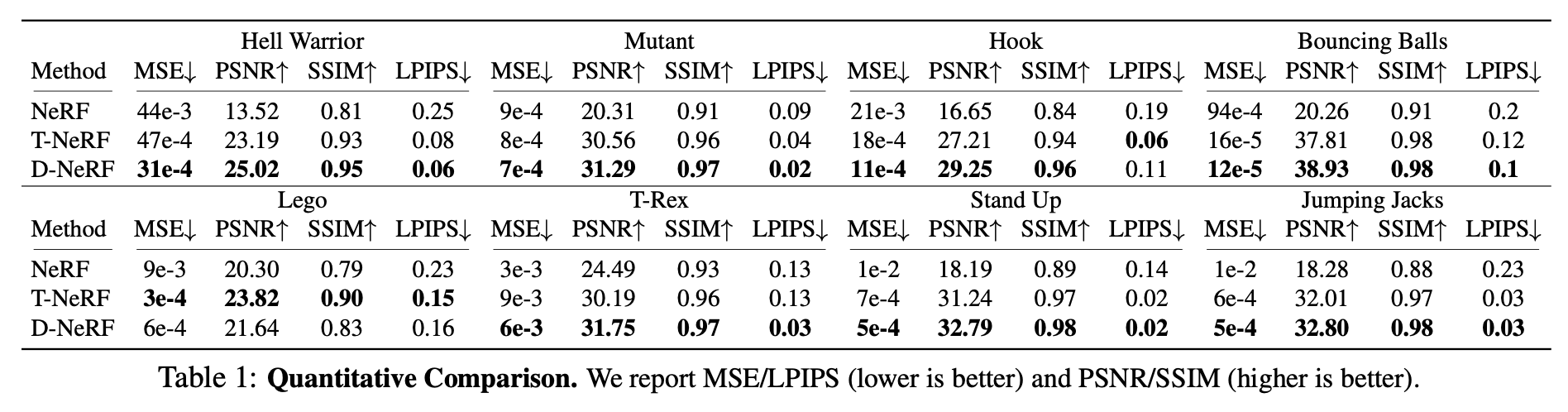
以下はNeRFとT-NeRF(canonical spaceを用いず、直接 radiance fieldで変位まで学習したもの?)、とのMSE, PSNR, SSIMの比較。
deformableなデータを用いているので、NeRFはこれに対応できず精度が悪い。T-NeRFとD-NeRFとではD-NeRFが若干よい。