はじめに
CVPR2019 に poster で accept された以下の論文
[1]D. Xiang, et. al, "Monocular Total Capture: Posing Face, Body, and Hands in the Wild"
のまとめ
arXivのリンク
https://arxiv.org/abs/1812.01598
コードは近日中に公開されるらしいが、現在(19/5/4)のところ見当たらず
以下、個人的に興味があるbody推定のロジック部分のみまとめ(手と顔の部分は省略)。
概要
- 単眼RGBカメラのみから体、手、顔の3次元モデルを復元した
- モデルの途中でPOFs(part orientation fields)を推定し、これと関節のヒートマップから3次元モデルを復元させる
- 複数フレームの情報を処理してtrackingも行う
位置付けとしては、去年CVPR2018で発表された Adam model[2] を単眼カメラでやった感じ。total captureと研究室も同じ。
以下が3D total body motion を生成した例。それぞれ左側が入力画像、右側が3D total body motion。

モデルの全体像
全体像は以下の図。

1)左から $i$ フレームの input image $I_i$ をCNNに入れて関節信頼度マップ(joint confidence map)$S$ とPOFs(part orientation fields) $L$ を出力する。
2)これらの情報を元に3次元メッシュモデル $\Psi_i$ を構築する。
3)これに前フレームの画像 $I_{i-1}$ や3Dモデル $\Psi_{i-1}$ を加えて時間方向に安定させ、3Dモデルの精度を上げる
POFs(part orientation fields)による3D骨格の推定
本手法の最大の特徴であるPOFs部分。
先にざっくり仕組みを概観すると、以下の図のように

各limbの親関節から子関節(図中の例では右肘から右手首)の3次元ベクトルをそれぞれ $x, y, z$ に分け、それぞれを1チャンネル内の値で表す。
細かく定義すると、まず
$\mathbb{S}$ :骨格のヒエラルキーで、親関節ー子関節のセットからなる
$J_m \in \mathbb{R}^3$ :親関節の3次元表示
$J_n \in \mathbb{R}^3$ :子関節の3次元表示
$P_{(m,n)}$ :カメラ座標における親関節から子関節へのベクトル
$\hat{P}_{(m,n)}$ :3次元座標における親関節から子関節への単位ベクトル・・・つまり
\hat{P}_{(m,n)} = \frac{J_n - J_m}{\| J_n - J_m \|}
これらを用いて POFs $L_{(m,n)} \in \mathbb{R}^{3 \times h \times w}$ を3チャンネルで表す。
L_{(m,n)}(x) = \begin{cases}
\hat{P}_{(m,n)} & if \ x \in P_{(m,n)} \\
0 & otherwise.
\end{cases}
この POFs は OpenPoseの PAFs によく似ている。実際、著者らはここまでのモデルをOpenPoseのPAFsの2チャンネルを3チャンネルに変更して使用している。
3D modelの構築
関節の信頼度マップと POFs から3D model を求める手順の概要は以下の図。

左端が関節の信頼度マップで、中央がPOFsで、この2つから3次元上の骨格の推定値が求まる。
これに対して予め用意した Adam モデルという人の3次元メッシュモデルとを近づけるように最適化する。
具体的には以下。
まず関節の信頼度マップは、body(B)だと $J$ 個ある。
\{ J_m^B \}^J_{m=1}
$S^B$ の各チャンネルの中で最大値となるピクセルをその関節の位置と推定する。
この関節のうち、親関節側から子関節側へPOFsの足跡を辿ることで対応する子関節を求める。(手法はOpenPoseのPAFsと同じ)
この3次元メッシュモデル $\Psi$ を規定する body motion parameters $\theta$ 、global translation parameter $t$ 、shape coefficients $\phi$ を以下の最適化問題を解くことで求める。
\mathcal{F}^B (\theta, \phi, t) = \mathcal{F}^B_{2D}(\theta, \phi, t) + \mathcal{F}^B_{POF}(\theta, \phi) + \mathcal{F}^B_p(\theta)
このうちまず $\mathcal{F}^B_{2D}$ は以下。
\mathcal{F}^B_{2D}( \theta, \phi, t) = \sum_m \| j^B_m - \prod(\tilde{J}^B_m ( \theta, \phi, t)) \|^2
ここで $\tilde{J}^B_m$ はAdam のモデル、$\prod$ は3次元から2次元へのprojection。
また $\mathcal{F}^B_{POF}$ は以下。
\mathcal{F}^B_{POF} (\theta, \phi) = w^B_{POF} \sum_{(m,n) \in \mathbb{S}} 1 - \hat{P}^B_{(m,n)} \cdot \tilde{P}^B_{(m,n)} (\theta, \phi)
ここで $\tilde{P}^B_{(m,n)}$ は Adam モデルにおける $P^B_{(m,n)}$ の単位ベクトル。
よって単位ベクトル同士の内積が1・・・・単位ベクトル同士が同じになるようにする。
また $\mathcal{F}^B_p(\theta)$ は以下。
\mathcal{F}^B_p(\theta) = w^B_p \| A^B_{\theta} ( \theta - \mu^B_{\theta} )\|^2
時系列処理による精度向上
以下が概要の図。
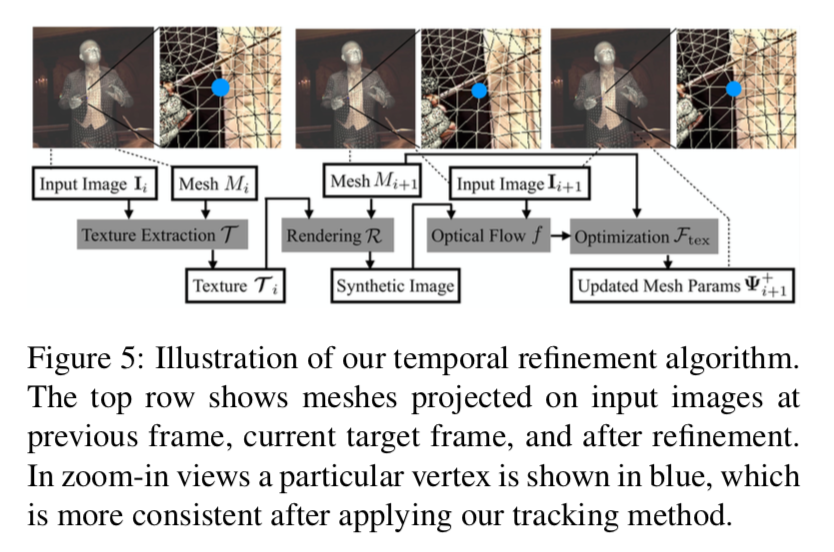
1)まず前の時刻 $i$ のメッシュ $M(\Psi_i)$ にはるテクスチャー $\mathcal{T}_i$ を入力画像 $I_i$ から求める。
\bf \mathcal{T} \rm _i = \mathcal{T} (I_i, M(\Psi_i))
このテクスチャー $\mathcal{T}_i$ は現時刻 $t+1$ でも変わらないと考える。
そうすると、 このテクスチャーを現時刻のメッシュ $M_{i+1}$ にはりつけたものを画像へ投影したもの $\mathcal{R} ( M_{i+1}, \mathcal{T}_i)$ (以下synthetic imageという)との差分が存在する。よってこれらからオプティカルフローを求める。
f_{i+1} = f(\mathcal{R} (M_{i+1}, \mathcal{T}_i), I_{i+1})
このオプティカルフロー関数に現時刻のメッシュ各頂点を投影したもの $v_n (i+1)$ を入力^し、求まった各頂点の投影座標と、現時刻のパラメータ $\Psi^{+}_{i+1}$ から求めた各頂点の投影座標との差を縮めるよう、パラメータを最適化する。
\mathcal{F}_{tex} (\Psi^{+}_{i+1}) = \sum_n \| v^{+}_n (i+1) - v^{'}_n (i+1) \|^2
これはメッシュを画像 $(x,y)$ へ投影した上での頂点同士のロス。z軸方向が加味されてない。よって以下のロスも加える。
\mathcal{F}_{\Delta z} (\theta^{+}_{i+1}, \phi^{+}_{i+1}, t^{+}_{i+1}) = \sum_m (J_m^{+z} (i+1) - J_m^z (i))^2
最終的に、トータルのロスは以下。
\mathcal{F}^{+} (\Psi^+_{i+1} ) = \mathcal{F}_{tex} + \mathcal{F}_{\Delta z} +\mathcal{F}_{POF} +\mathcal{F}^F
reference
[2] H. Joo, T. Simon, and Y. Sheikh. Total capture: A 3d de- formation model for tracking faces, hands, and bodies. In CVPR, 2018.