はじめに
NIPS2017から A. Kosiorek らの HART Hierarchical Attentive Recurrent Tracking をまとめてみた。
論文はこちら
http://papers.nips.cc/paper/6898-hierarchical-attentive-recurrent-tracking.pdf
著者らのコードはこちら。Tensorflowで書かれてます。
https://github.com/akosiorek/hart
要点
- クラスを特定しない状況下でのトラッキングモデルである
- 大脳皮質を真似て「どこ」と「なに」を判断する流れを分けることで不必要な特徴量を排除した(階層的注目点再帰モデル)
- 具体的にはattention層で注目点以外のバックグラウンドの情報を捨て、その後の層で対象物体に限定した特徴量を調整する
モデルのアーキテクチャ
モデルの全体像は以下のような感じ。
 【図1 全体的な流れ 論文P3のFigure 2より】
【図1 全体的な流れ 論文P3のFigure 2より】
全体的な流れ
図1で、まず画像 $x_t$ を入力し、Spatial Attention のしくみにより $g_t$ を得る。これを V1 & Ventral Stream に送り特徴量 $\nu_t$ を得る。一方 Dorsal Stream では対象物体か否かをセグメントする $s_t$ を出力する。この $\nu_t$ と $s_t$ とのHadamard 積から masked featuresである $v_t$ を求める。これをLSTMに入力することで出力 $o_t$ を得る。$o_t$ と $s_t$ をMLP(全結合層)に入力して attention $a_{t+1}$ 、appearance $\alpha_{t+1}$ 、矩形の集合 $\Delta \hat{b}_t$ を求める。
図1において実線は同時刻の流れ、破線は1時刻経た流れである。以下、それぞれのパーツごとに見ていく。
Spatial Attention
まず入力画像を $\bf{x}_t \in \mathbb{R} ^{H \times W}$ とする。
これに対して行列 $\bf{A}_t^x \in \mathbb{R} ^{w \times W} $ と $\bf{A}_t^y \in \mathbb{R} ^{h \times H} $ を作成する。これら行列の各行は Gaussian となっている。
出力 $\bf{g}_t \in \mathbb{R} ^{h \times w}$ は
\bf{g}_t = \bf{A} ^y_t x_t (A^x_t)^T
となる。具体的に $\bf{A}^x_t$ などの作成方法は以下。
図1でt時刻におけるLSTMからMLPを経た出力 $\bf{a} _{t+1}$ が t+1 時刻におけるspacial attention の情報を保持している。
具体的には $\bf{A}^x_t$ などの各行における Gaussian の平均やstrideである。これによって
A _t^X[i,a]=\exp(-\frac{(a-\mu ^i_X)^2}{2\sigma ^2})
みたいな感じで作成する。ここで分散 $\sigma$ はよくわからんが、strideとの関係を事前に線形回帰で求めておくみたい?以下の図1−2において緑の矩形は $g_t$ 、赤の矩形は予測した対象物体の矩形、青の矩形は ground-truth。
 【図1−2 モデルの出力の例 論文P2のFigure 1より】
【図1−2 モデルの出力の例 論文P2のFigure 1より】
glimpse $g_t$ がより大局的に捉えられている。
Appearance Attention
このステージは以下の図2のようになる。
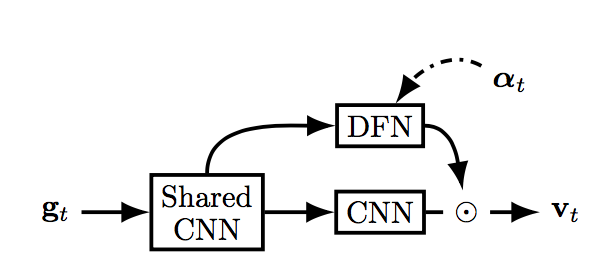
【図2 Appearance Attentionの模式図 論文P4のFigure 3より】
これは以下のような脳の視覚野を模している。

【図3 視覚野 wikipediaから引用】
glimpse $g_t$ は V1(Shaerd CNN)に送られる。図3では後頭部の灰色の部分。ここでは以下のようにCNNで畳み込まれる。
\mathbb{R} ^{h \times w} \to \mathbb{R} ^{h_{v} \times w_{v} \times c_{v}}
次に二手に分かれて、一方はDFN(dorsal stream:図3では緑色の経路)、もう一方はCNN(ventral stream:図3では紫色の経路)へと進む。
ventral stream ではCNNで画像の特徴量 $\nu _t$ を抽出する。
一方、dorsal stream では空間的な関係を処理する。それぞれの領域が追跡している対象物体であるか否かを Bernoulli 分布 $s_t$ で出力する。
この時使う畳み込みのフィルターはLSTM→MLPからのt時刻の出力 $\alpha _{t}$ を用いて
\Psi _t=(\psi _t^{a_i \times b_i \times c_i \times d_i})^K_{i=1}=MLP(\alpha_t)
として求める。MLPは全結合層。
$\nu _t$ と $s_t$ から $v_t$ を以下のように求める。
v_t = MLP(vec(\nu_t \odot s_t))
$\odot$ はHadamard積。
State Estimation
言うまでもなく、目的は過去の状態や推定した矩形情報、及び現在の画像情報から現在の矩形の位置を求めることだ。
過去の状態はLSTMの hidden state に担わせる。
o_t, h_t = LSTM(v_t, h_{t-1})
この $o_t$ とdorsal stream からの出力 $s_t$ を用いて現時刻の対象物体の矩形 $\hat{b}_t$ と次時刻の $\alpha _{t+1}$ 等は以下で求める。
\alpha _{t+1}, \Delta a_{t+1}, \Delta \hat{b}_t = MLP(o_t, vec(s_t))\\
a_{t+1}=a_t + tanh(c)\Delta a_{t+1}\\
\hat{b}_t=a_t + \Delta \hat{b}_t
Lossの計算
まずLoss全体 $L_{HART}$ は以下。
L_{HART}(D,\theta)=\lambda _t L_t(D, \theta)+\lambda _s L_s(D, \theta)+\lambda _a L_a(D, \theta)+R(\lambda)+\beta R(D,\theta)
$\theta$ はネットワークのパラメータ。R(・)は正則化項。Dはデータセットで
D=(({\bf{x}}_{1:T},{\bf{b}}_{1:T})^i )^M_{i=1}
と M 個のビデオデータの中にそれぞれ T 系列の画像がある。次に各項の詳細。
TrackingのLoss
IoUを
IoU(a,b)=\frac{a \cap b}{a \cup b}=\frac{area \ of \ overlap}{area \ of \ union}
として、
L_t=(D,\theta)={\mathbb{E}}_{p(\hat{b}_{1:T}|{\bf{x}}_{1:T},b_1)}(-\log IoU({\hat{b}}_t,b_t))
つまりIoUのnegative logに対する全データ・全系列に渡る平均。$b_t$ は対象物体の実際の矩形。
Spatial Attention の Loss
$L_t$ だけだと以下のような問題点がある。例えば、 $t=t$ で対象物体が途中でほとんど隠れてしまう場合、MLPからの出力は ${\Delta}{\hat{b}_t}$ がほぼ領域なし。
$a_{t+1}$ もほぼ領域なし、となるだろう。
そうすると、この $a_{t+1}$ が $t=t+1$ でfeed backされて glimpseの推定に使われるので、その後の矩形の推定が困難になるだろう。
そこで $a_t$ が ${\hat{b}}_t$ を大局的に拾えるような演算をLossに加える。
L_s (D,\theta)={\mathbb{E}}_{p(a_1:T|{\bf{x}}_1:T,b_1)}\left[ -{\log} \left(\frac{a_t \cap b_t}{area(b_t)} \right) - \log \left( 1-IoU(a_t, x_t) \right) \right]
第1項において $a_t$ は $b_t$ を含んでいれば任意の大きさでよくなるが、第2項目で大きくなりすぎないように制約している。
これによって、 $a_t$ は $b_t$ が小さい時でもそれを包含する適度な大きさになるということか???
Appearance Attention の Loss
これに関してはイマイチ理解してないが、とにかく appearance attention を対象物体だけ捉えるマスクとなるように以下の Loss を加える。
L_a (D, \theta)={\mathbb{E}}_{p(a_1:T,s_1:T|{\bf{x}}_1:T,b_1)} [H(\tau (a_t,b_t),s_t)]
ここで $H$ は交差エントロピー、$\tau$ は $\tau (a_t,b_t) : {\mathbb{R}}^4 \times {\mathbb{R}}^4 \to (0,1) ^{h_v \times w_v}$ となる写像。
正則化項
L2ノルムで正則化する。
R(D,\theta)=\frac{1}{2}\| \theta \|^2_2 + \frac{1}{2}\| {\mathbb{E}}_{p(\alpha _1:T,s_1:T|{\bf{x}}_{1:T},b_1)} \|^2_2
Adaptive Loss Weights
ハイパー・パラメータの調整を避けるため以下の正則化も加える。
R(\lambda)=-\sum _i \log (\lambda^{-1}_i)