はじめに
去年暮れにarXivに載った以下の論文
[1]J. Li, et. al. "CrowdPose: Efficient Crowded Scenes Pose Estimation and A New Benchmark"
のまとめ
journalやconferenceは不明。
arXiv:
https://arxiv.org/abs/1812.00324
既にざっくりまとめたブログが存在した。
https://engineer.dena.jp/2019/04/cv-papers-19-human-recognition.html
概要
- オクルージョンなどが多い密集した場面での多人数に対する姿勢推定をtop-down方式で行うモデル
- 始めに人の領域を切り抜き(SPPE)、その中に含まれる対象人の関節及び、他の人の関節を推定し、その後広域に骨格と骨格を関連づける
- 密集した場面での多人数に対する姿勢推定に特化したデータセットを公開
以下の図では、左側がtop-down方式でのstandard である mask-RCNN、右が本提案手法。

比べると、人が密集した場面では本手法の方がよい。
背景
現在pose estimation で主流の手法は、以下のグラフのように人が密集すればするほど精度が落ちる。
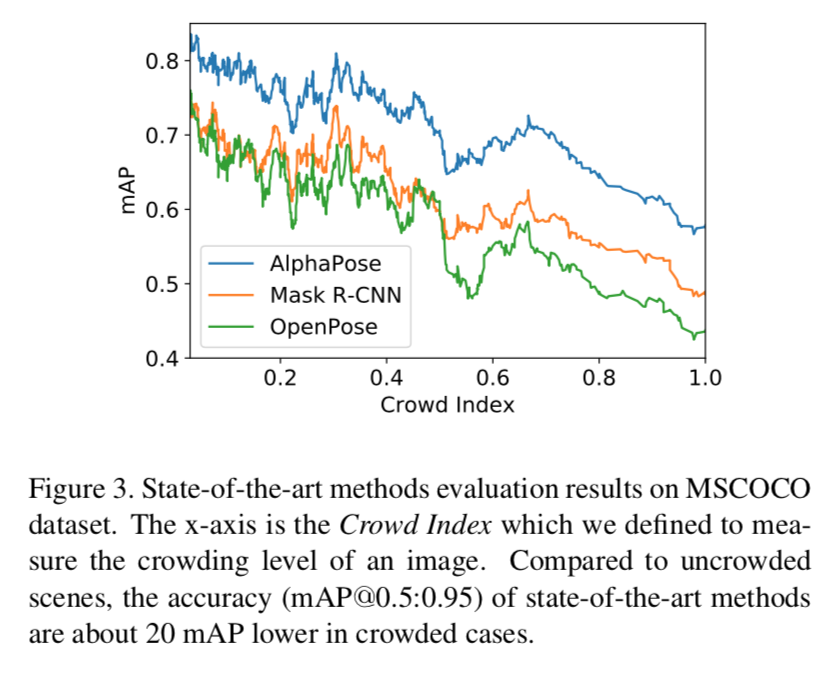
このグラフは横軸がcrowd index(後述)、縦軸がmAP。
よく使われるAlphaPose、Mask-RCNN、OpenPoseでみると、いずれも密集度合い(crowd index)が増すにしたがってmAPが大きく落ちている。
これは評価でよく使われるmicrosoft COCO dataset などが密集した場面が少なく、それに適応するように学習されてるからである。
一方で、スポーツのシーン解析や街中での自動運転を想定した場合、人が密集した場面が多い。
本手法はこのような密集した場面に力を発揮する手法である。
提案手法の全体像
以下が提案手法の全体像。

1)まず画像に対して各人の領域を切り抜く(jc-SPPE;joint-candidate single person pose estimator)。この矩形内には対象人の関節も、周囲の人の関節も存在する。(図の左半分)
2)これに対して各矩形の対象人とその関節を矩形を超えた広域で結びつけ(Global Association)、最終的なposeを決定する。(図の右半分)
jc-SPPE
これまでのSPPE(single person pose estimator)だと、骨格の形成が矩形内にある関節に限定されていた。
jc(joint-candidate)-SPPEでは、矩形周囲の人の関節も残す。
loss
そのためlossには矩形の対象人以外の関節も推定するように設計する。
以下定義
${\bf{P}}_i^k$ :モデルが推定する矩形対象人 $i$ 人の関節 $k$ 番目の heatmap
${\bf{T}}_i^k$ :矩形対象人 $i$ 人の関節 $k$ 番目の heatmap の target
${\bf{C}}_i^k$ :矩形対象人 $i$ 人以外人の関節 $k$ 番目の heatmap の target
target ${\bf{T}}_i^k$ は関節の中心 ${\bf{p}}_i^k$ を中心とし、スケール $\sigma$ とするガウシアンで作成する。
{\bf{T}}_i^k = G({\bf{p}}_i^k|\sigma)
target ${\bf{C}}_i^k$ は関節の中心 ${\bf{p}}_i^k$ を中心とし、スケール $\sigma$ とするガウシアンを矩形内の全ての対象外人の全ての間接にわたって足し合わせた混合ガウス分布とする。
{\bf{C}}_i^k = \sum_{p \in \Omega^k_i } G({\bf{p}}|\sigma)
loss は以下のように対象外人のheatmapも考慮したMSEとする。
Loss_i = \frac{1}{K} \sum^K_{k=1} MSE [{\bf{P}}_i^k, {\bf{T}}_i^k+\mu {\bf{C}}_i^k]
$\mu$ は $[0,1]$ 内の値だが、実験では $0.5$ を用いている。
骨格形成のロジッック
骨格のグラフの定義
まず bounding box の対象人に対するノード $\mathcal{H}$ を以下とする。
\mathcal{H} = \{h_i:\forall i \in \{ 1 \ldots M \} \}
$M$ は人の数。
次に間接に対するノード $mathcal{J}$ を以下とする。
\mathcal{J} = \{ v_j^k : {\rm for} \ k \in \{ 1,\ldots ,K \},j \in \{ 1, \ldots , N_k \} \}
$k$ は間接位置で、その $j$ 番目のnode を $v_j^k$ としている。
bounding box の対象人と各間接候補を結ぶのがエッジ $\mathcal{E}$ 。
人のノード $h_i$ と関節のノード $v_j^k$ を結ぶエッジは
\mathcal{E} = \{ e^k_{i,j} : \forall i,j,k \}
となる。エッジ $e^k_{i,j}$ の応答スコアを $w^k_{i,j}$ で表す。
骨格を表すグラフはこれらノードとエッジから構成される。
\mathcal{G} = ((\mathcal{H}, \mathcal{J}),\mathcal{E})
最適化
以下の目的関数を最大化する。
\begin{eqnarray}
\max_d \mathcal{G} &=& \max_d \sum_{i,j,k} w^{(k)}_{i,j} \cdot d^{(k)}_{i,j} \\
s.t. & & \sum_j d^{(k)}_{i,j} \leq 1, \forall k \in \{ 1, \ldots , K \}, \forall j \in \{ 1, \ldots , M \} \\
& & \sum_j d^{(k)}_{i,j} \leq 1, \forall k \in \{ 1, \ldots , K \}, \forall j \in \{ 1, \ldots , N_k \} \\
& & d^{(k)}_{i,j} \in \{ 0, 1 \} \forall i,j,k \\
\end{eqnarray}
最終的に採用する edge が $d^{(k)}_{i,j} = 1$ となり、不採用が $0$ となる。
条件の1つ目から、任意の人ノードは関節 $k$ に関して2つ以上とは繋がらなくなる。
条件の2つ目から、任意の関節ノードは2人以上とは繋がらなくなる。
この目的関数を各人のグラフ $\mathcal{G}_k$ に分解して
\begin{eqnarray}
\max_d \mathcal{G} &=& \max_d \sum_{i,j,k} w^{(k)}_{i,j} \cdot d^{(k)}_{i,j} \\
&=& \sum^K_{k=1} (\max_{d^{(k)}} \sum_{i,j} w^{(k)}_{i,j} \cdot d^{(k)}_{i,j}) \\
&=& \sum^K_{k=1} \max_{d^{(k)}} \mathcal{G}_k
\end{eqnarray}
として、最後の式を解く。
crowd index
新たに提案した crowd index は以下。
Crowd \ index = \frac{1}{n}\sum_{i=1}^n \frac{N^b_i}{N^a_i}
$N^a_i$ は $i$ 番目の人の矩形の中に入っている、その人のjointの数で、 $N^b_i$ は矩形内の別の人のjointの数。
よって $\frac{N^b_i}{N^a_i}$ は人が密集すればするほど他の人の関節が近傍にきて、矩形内に入るので、値が大きくなる。
$Crowd \ index$ はこれを全ての人で平均化したもの。