はじめに
CVPR2017 から以下の論文
[1] G. Papandreou, et. al. "Towards Accurate Multi-person Pose Estimation in the Wild"
のまとめ
ちょっと古いが、その後にPersonLabやPifPafに与えた影響を考慮して、decoderのロジック部分を中心にまとめ
arXiv:
https://arxiv.org/abs/1701.01779
概要
- top-down 方式で姿勢推定を行うモデル
- これまでのheatmap方式を2つのstageに分解し、1つをkeypoints周辺領域の推定、他の1つを近傍のkeypointsの位置を推定されるようにした。
- 以上の手法を用いることで、2017年初頭あたりで COCO keypoints dataset でSOTAを達成。
アーキテクチャの全体像
以下の図が全体像。
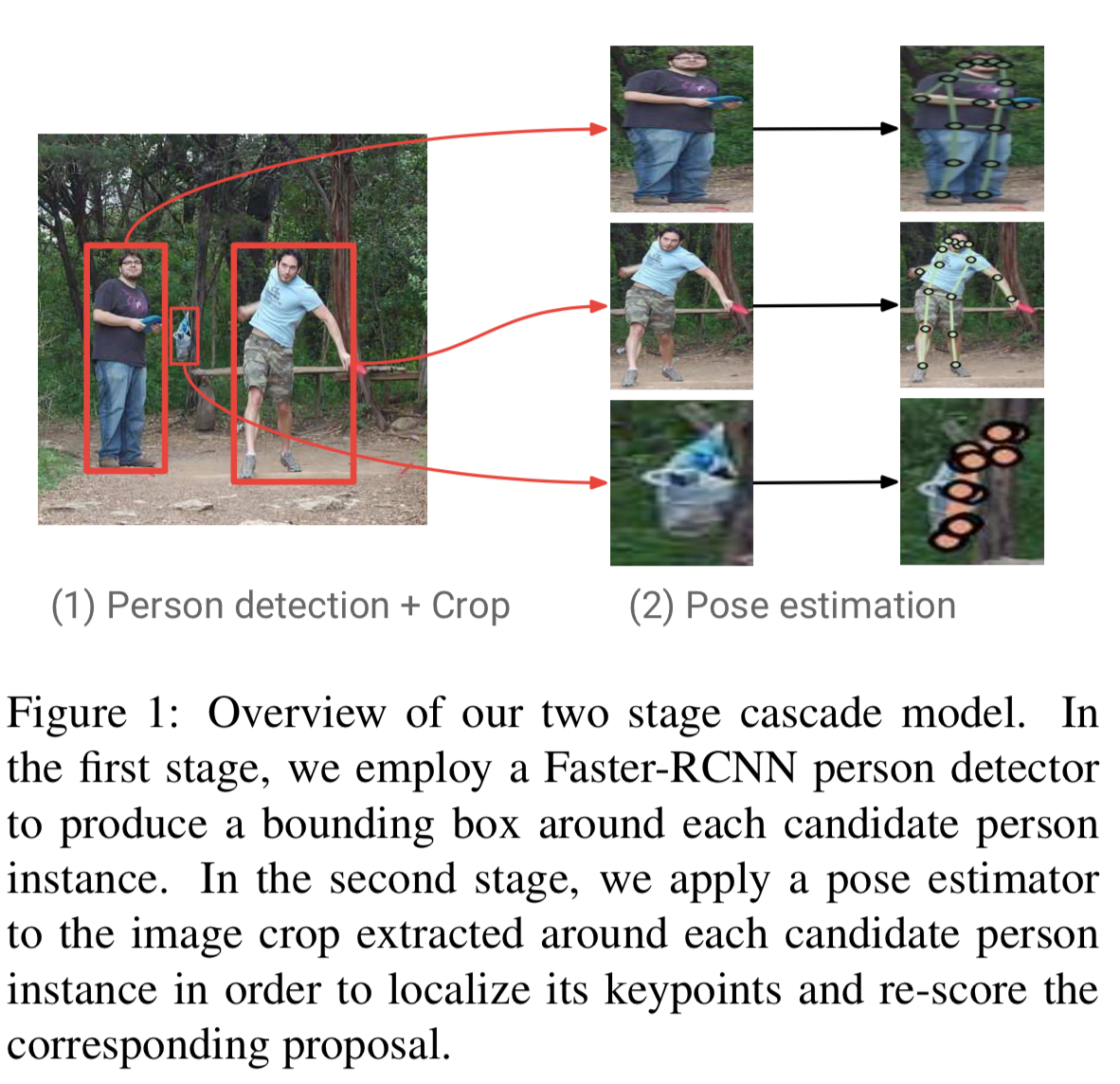
top-down形式なので、上手のように2段階に分かれる。
1段階目で画像から各人のbounding box を切り取る。
2段階目で切り取った人の画像から姿勢を推定する。
この論文では1段階目のベース・モデルはFaster-RCNN、2段階目のベース・モデルはResNet。
姿勢推定アーキテクチャ
2段階目の姿勢推定の詳細。
従来の keypoints の推定方法
まず従来の keypoints の推定方法をおさらい。主に以下の2つ。
(1) DeepPose [2] によって提案された手法で、画像を入力して、各 keypoints の相対座標を数値として出力させる。つまり回帰問題として解く手法。
この手法では、画像に2人以上が入った場合、同じ keypoints が2つ以上となり、正しい相対座標が推定されない。
(2) [3] により提案された手法で、各keypointsのheatmap的なものを出力する。つまり各pixelはkeypointsか否かの分類をしてるようなもの。
これにより2つ以上の keypoints が存在する場合に対応できるようになったが、mapが特徴量の大きさに依存するため粗くなる。例えば、通常畳み込んで畳み込んで、出力の時点では特徴量が8x8とか20x20のようになるが、これで画像上の正確な位置を示すのは困難。
提案手法の概要
本論文の提案手法は上記(2)の問題を解決するもの。
モデルからは以下の2種類を出力する。
- 各keypoint から 半径 R ピクセルにあるか否かを表す heatmap(1チャンネル)
- 近傍にある各keypoint の位置を表すベクトル(2チャンネル)
この3チャンネルをcoco dataset だと 17 keypoints に対して出力するので、出力チャンネルは $ 3 \times 17 = 51$ 。
例えば以下の図では

フェデラ〜?の左肘に対して一定の半径となるheatmap(中央)を推定するのと同時に、その半径内のピクセルは肘の正確な位置をベクトルで推定する(右)
提案手法の詳細
まず
$h_k (x_i)$ :画像 $x$ 中のピクセル $x_i$ における $k$ 番目のkeypintのheatmap
$l_k$ :keypoint $k$ の正確な位置
として、あるピクセル $x_i$ が keypointの正確な位置から半径 $R$ 以内ならそのピクセルの heatmap を1とする。つまり
h_k (x_i) = 1 \ \ if \ \| x_i - l_k \| \leq R
またkeypointsの正確な位置を指すベクトル (offset vector) は
F_k(x_i) = l_k - x_i
とする。これらheatmap、および offset vector から正確なkeypointの位置を計算する。
これはより正確なheatmap・・・highly localized activation map $f_k (x_i)$ は以下で求める。
f_k(x_i) = \sum_j \frac{1}{\pi R^2} G( x_j + F_k(x_j) - x_i) h_k (x_j)
ここで $G$ は bilinear interpolation kernel。
$G$ のカッコの中は $x_j + F_k(x_j) - x_i = l_k - x_j$ なので任意点 $x_j$ から keypoint推定位置 $l_k$ へのベクトル。これに対して bilinear interpolation kernel をとっている。
これに $h_k(x_j)$ をかけてるので、keypointから半径 $R$ の円(と推定された位置)のみを対象としている。
この円は正確に推定されると $\pi R^2$ の面積があるので、それで割って正規化している。
これを全ての $j$ に対して足し合わせることで、$x_j$ における highly localized activation map $f_k (x_i)$ を算出している。
これを図で表すと以下。

reference
[2] A. Toshev and C. Szegedy. Deeppose: Human pose estima- tion via deep neural networks. In CVPR, 2014.
[3] A.Jain,J.Tompson,M.Andriluka,G.Taylor,andC.Bregler. Learning human pose estimation features with convolutional networks. In ICLR, 2014.