はじめに
2、3日前 arXiv にあがったこちらの論文
[1] W. Song, et. al. "T-Net: A Template-Supervised Network for Task-specific Feature Extraction in Biomedical Image Analysis"
のざっくりしたまとめ
arXiv:
https://arxiv.org/abs/2002.08406
提出先の journal 等は不明。
概要
- 医療系画像に対して診断や物体検出、セグメントなどをするモデル
- まず template を使ってencoderのみを学習させる
- その後事後ネットワークを追加して、様々なタスクに対応させる
背景
医療系のタスクでは encoder-decoder なアーキテクチャをベースとする U-Net系のモデルが使われる事が多い。これに対して筆者らは以下の3点で問題だと考えている。
- encoder-decoder をbackpropさせると勾配はdecoder経由でしか伝わらないので、encoderの学習が弱い
- encoderとdecoderは通常、対称な形状なのでencoderの2倍の計算コストがかかる。よって高解像度の画像を学習させるのは難しい
- segmentation では教師として単純な2値の target を使用するが、これがencoderの特徴量抽出能力を制限している
本手法
手法の全体像
全体像は以下の図のよう。

template により encoder を直接学習させる
通常のencoder-decoder なアーキテクチャだと以下のように
\min_{\theta_e, \theta_d} Loss \left( f_d \left( \theta_d, f_e \left( \theta_e, I \right) \right), I^B \right)
入力画像 $I$ を encoder $f_e$ (パラメータは $\theta_e$ )でエンコードし、それを decoder $f_d$ (パラメータは $\theta_d$ )でデコードして出力とする。
これと target $I^B$ とで Loss を計算し、それを勾配降下法等で最小化させる。
よってエンコーダのパラメータにおける勾配は
\frac{\partial Loss}{\partial \theta_e} = \frac{\partial Loss}{\partial f_d} \cdot \frac{\partial f_d}{\partial f_e} \cdot \frac{\partial f_e}{\partial \theta_e}
とdecoder 経由になる。
一方で本手法 T-Net はencoder を template $T$ で学習するので、
\min_{\theta_e} Loss \left( f_e \left( \theta_e, I \right), T \right)
である。よってエンコーダのパラメータにおける勾配は
\frac{\partial Loss}{\partial \theta_e} = \frac{\partial Loss}{\partial f_e} \cdot \frac{\partial f_e}{\partial \theta_e}
とdecoderを経由しないですむ。
template
では、その template はどのようなものを用いるか。
以下の図では3つの template が提示されている。

1つの制約は、encoderからの出力に対する target なので、小さなサイズのものであること。
なので、図の右側1番上(NN down-sampling)では単純に nearest-neighbor interpolation で小さくしている。
それにガウシアンをかけたものが上から2番目の Gaussian filter 。これにより対称物体の境界外の領域にも注意を払うようになる。
下側の Distance map は境界からの距離が遠い(つまりより物体の中央あたりにある領域)ほど高い値になるようにしたもの。
ネットワークのアーキテクチャ
アーキテクチャの概略図は以下。

ざっと見て、一番上でtemplate を使った encoder の学習を行なっている。
下側左ではそれにU-Net的な Up-sampleing Networkを加えてsegmentを出力している。
一方、下側右では encoder にdetection Network を加えて location map を出力している。
ベースは dense block
encoder および decoder では以下の dense block を用いる。
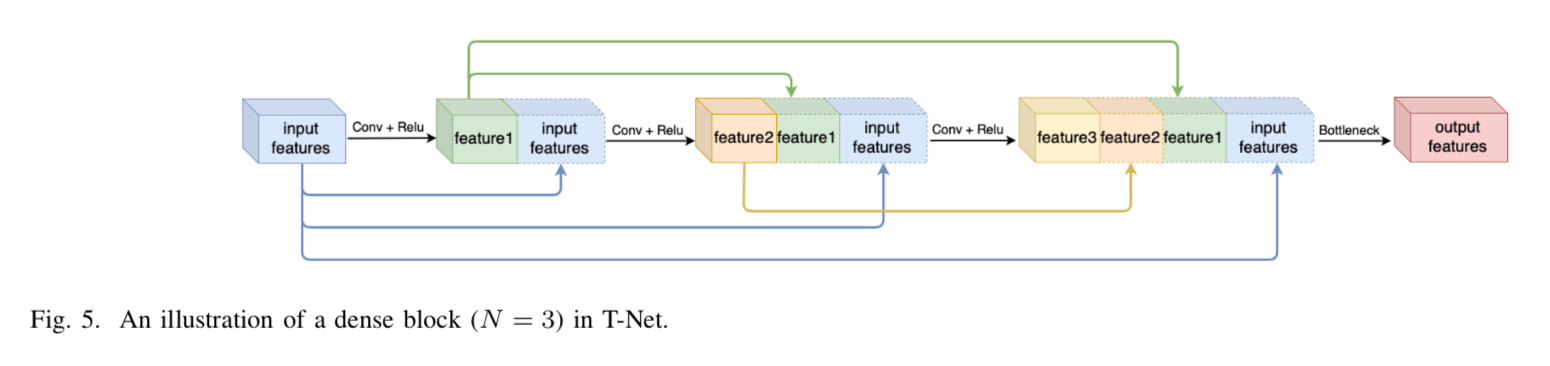
encoder network
図を見たら一目瞭然だが、あえて encoder を細かく見ると、


となる。初めに conv して、その後1回 dense blockした後に max-poolingでdown-sampling して、更に2回 dense block した後に down-sampling、最終的に5つの dense block を経る。
Up-sampling Network
segment用のup-sampling ネットワークは以下。

ほぼほぼ U-Net の decoder 部分と同じ。
Detection Network
detection 用のネットワークは以下。

encoder から抜いてきた複数のスケールの feature map を concat して、detection network に入れる。
複数スケールを使うが、それらは resize して同じ大きさにしてから concate し入力する。最終的には出力層は最後の1つなので、SSD系よりは YOLO 系に近い構造。
Loss
1. template loss
まず encoder を学習させる template loss は以下の通常の dice loss。
Loss_{tem} = 1 - \frac{1}{N_T} \sum^{N_T}_t \frac{2 \sum^{H_T}_i \sum^{W_T}_j p_{i,j,t} g_{i,j,t}}{\sum^{H_T}_i \sum^{W_T}_j p^2_{i,j,t} + \sum^{H_T}_i \sum^{W_T}_j g^2_{i,j,t}}
$ g_{i,j,t} $ は ground truth 、$ p_{i,j,t} $ は prediction 。
Up-sampling loss
セグメント時の Up-sampling loss は以下。
上記と同じ dice loss。
Location loss
まず detection 時は物体位置の中心のみを推定する。(矩形を推定しないのはなぜ??)
出力グリッド $(i,j)$ に中心がある確信度 $c_{i,j}$ とそのオフセット $x_{i,j}$、$y_{i,j}$ を用いて loss は以下。
Loss_{det} = \sum^{H_L}_i \sum^{W_L}_j w_{i,j} ( c_{i,j} - \bar{c_{i,j}} )^2 + \sum^{H_L}_i \sum^{W_L}_j \mathbb{I}^{obj}_{i,j} \left[(x_{i,j} - \bar{x_{i,j}}^2 + (y_{i,j} - \bar{y_{i,j}}^2 \right]
中心がある確信度、オフセット共に MSE で loss を求める。中心がある確信度には重み $w_{i,j}$ をかけて修正している。
実験と結果
- Datasets:1)BraTS for 3D Tumor Segmentation, 2)MoNuSeg for 2D Nuclei Segmentation
- segmentation 時の metrics:1) Dice score, 2)ハウスドルフ距離
- detection 時の metrics:1)ED
ハウスドルフ距離
ハウスドルフ距離(Hausdorff distance)というものを初めて聞いたので、Wikipediaで調べてまとめ。
以下の図のように
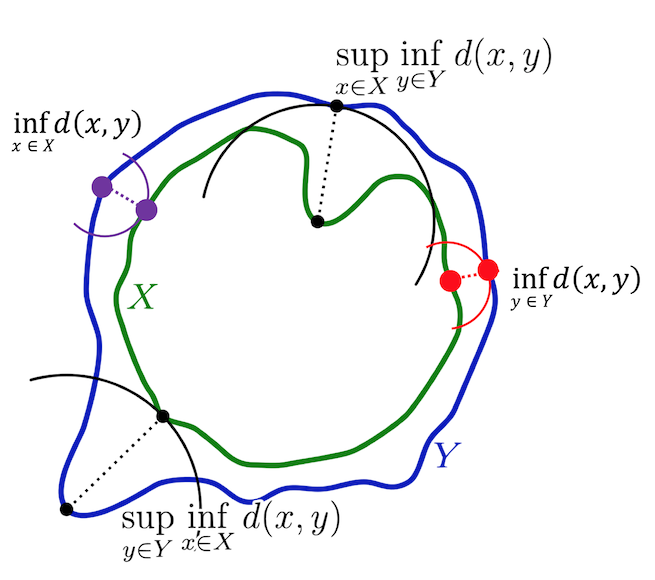
target の物体境界 $Y$ に対して predict した物体境界 $X$ がある時、$X$ 上の任意の点 $x$ と $Y$ 上の任意の点 $y$ との距離は $d(x,y)$。
今、ある $y \in Y$ を考え、これと任意の $x \in X$ との距離の中で下限は $\inf_{y \in Y} d(x,y)$ (上図の左側の紫点の距離)
これを全ての $x \in X$に対して求めた時に、その上限は $\sup_{x \in X} \inf_{y \in Y} d(x,y)$。(上図の下側の2つの黒点の距離)
一方、$x$ と $y$ を入れ替えて $\sup_{y \in Y} \inf_{x \in X} d(x,y)$ も求める。
この時、両者で大きい方をハウスドルフ距離とする。つまり
D_H (x,y) \equiv \max \{ \sup_{x \in X} \inf_{y \in Y} d(x,y) , \sup_{y \in Y} \inf_{x \in X} d(x,y) \}
要するに、2つの境界で最も距離のある位置関係における距離はいくらか、ってこと。
セグメンテーションタスクにおける他の手法との比較
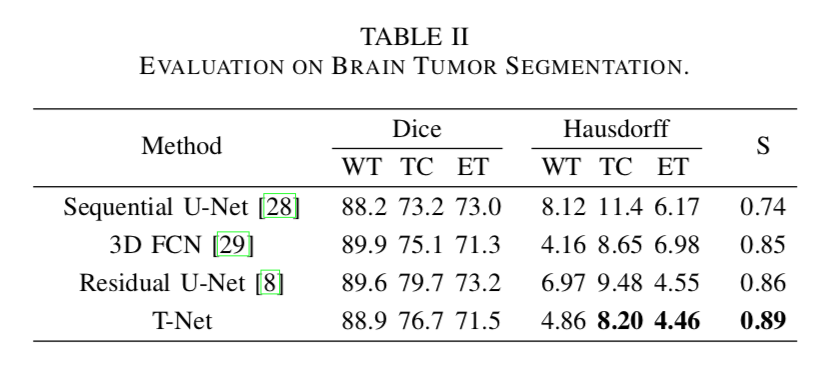
他の手法と比較して dice-score はイマイチだが、ハウスドルフ距離はいい。
以下は定性的評価。

detection タスクにおける他の手法との比較
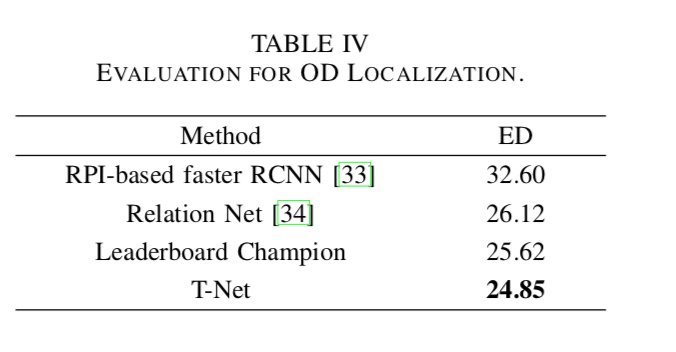
他の手法との中心位置におけるユークリッド距離での比較。
最も良い。