はじめに
ちょっと古いけど、NVIDIAのチームらが出した
[1]T. Wang, et. al. "Video-to-Video Synthesis"
のまとめ
-
githubの著者コード
https://github.com/NVIDIA/vid2vid
概要
- セグメントのシーケンスから動画を生成したり、動画の一部を変換した動画を生成したりするモデル
- 時系列な過去の情報や optical flow を使って各フレームの画像を生成する
以下が生成例。

説明にも書いてるが、左上が入力のセグメンテーション画像、その右が pix2pixの結果、左下が COVSTの結果、右下が本手法の結果。
過去の情報を使ってる分白線とかが滑らか。
手法
定義
${\bf s}_1^T = \{ {\bf s}_1, {\bf s}_1, \cdots , {\bf s}_T,\}$ ・・・セグメンテーションの各シーケンス
${\bf x}_1^T = \{ {\bf x}_1, {\bf x}_1, \cdots , {\bf x}_T,\}$ ・・・元動画のシーケンス
$\tilde{{\bf x}}_1^T = \{ \tilde{\bf x}_1, \tilde{\bf x}_1, \cdots , \tilde{\bf x}_T,\}$ ・・・ ${\bf s}_1^T$ を入力した時の動画のシーケンスの予測値
目標
目標はセグメンテーション・シーケンス ${\bf s}_1^T$ を入力として与えた時の動画の予測値 $\tilde{{\bf x}}_1^T$ の分布を正解の動画 ${\bf x}_1^T$ の分布に近づけること。つまり
p(\tilde{{\bf x}}_1^T | {\bf s}_1^T) = p({\bf x}_1^T | {\bf s}_1^T)
が目標。
generator
GeneratorはMarkov性を仮定して、過去 $L$ フレームの情報から生成させる
\begin{eqnarray}
p(\tilde{{\bf x}}_1^T | {\bf s}_1^T) &=& \prod^T_{t=1} p(\tilde{{\bf x}}_t | \tilde{{\bf x}}^{t-1}_{t-L}, {\bf s}_{t-L}^{t}) \\
\end{eqnarray}
つまり、過去 $t-L$ フレームから $t - 1$ までのgenerator自身の生成動画 $\tilde{{\bf x}}^{t-1}_{t-L}$ と過去 $t-L$ フレームから現在 $t$ のセグメンテーションのシーケンス ${\bf s}_{t-L}^{t}$ を入力とし、現在の生成動画 $\tilde{{\bf x}}_t$ を得る。
本論文の場合、$L=2$ をとるので、
\begin{eqnarray}
p(\tilde{{\bf x}}_1^T | {\bf s}_1^T) &=& \prod^T_{t=1} p(\tilde{{\bf x}}_t | \tilde{{\bf x}}^{t-1}_{t-L}, {\bf s}_{t-L}^{t}) \\
&=& \prod^T_{t=1} p(\tilde{{\bf x}}_t | {\bf x}_{t-1}, {\bf x}_{t-2}, {\bf s}_{t-1}, {\bf s}_{t-2}) \\
&=& p(\tilde{\bf x}_T | \tilde{\bf x}_{T-1}, \tilde{\bf x}_{T-2}, {\bf s}_{T-1}, {\bf s}_{T-2}) \cdots p(\tilde{{\bf x}}_1 | \tilde{\bf x}_{0}, {\bf s}_{0})\\
\end{eqnarray}
って感じ。
$L=2$ でフレーム $t$ からフレーム $t+1$ にかけてはこんな感じ。
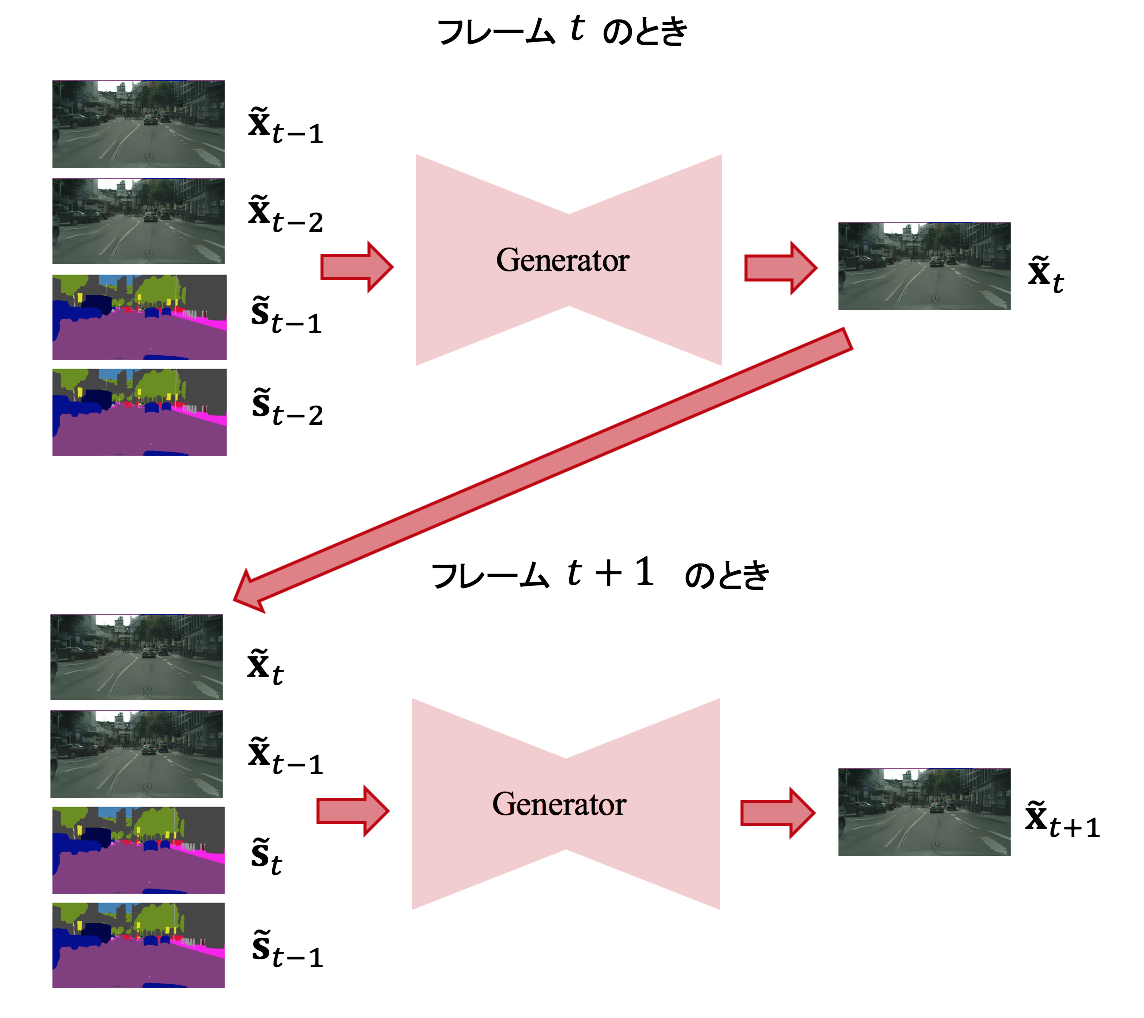
optical flow な部分とそれ以外との分離
generator の内部を更に詳しく見ると、
- optical flow に基づいて推定する部分
- optical flow では表現できない ocullusion の部分
に分けて考えていて、2 に関しては generator の想像力で生成する。
具体的には
- $\tilde{\bf w}_{t-1} = W(\tilde{\bf x}_{t-L}^{t-1}, {\bf s}_{t-L}^{t})$ ・・・$t-1$ フレームから $t$ フレームへの optical flow で、$W$ はそれを推定するネットワーク。
- $\tilde{\bf h}_t = H(\tilde{\bf x}_{t-L}^{t-1}, {\bf s}_{t-L}^{t})$ ・・・occulusion で見えてない部分を推定した画像。$H$がそれに相当する image hallucinatio network。
- $\tilde{\bf m}_t = M(\tilde{\bf x}_{t-L}^{t-1}, {\bf s}_{t-L}^{t})$ ・・・occulusion mask。[0,1]の連続値。
として
F(\tilde{\bf x}_{t-L}^{t-1}, {\bf s}_{t-L}^{t}) = ({\bf 1} - \tilde{\bf m}_t ) \odot \tilde{\bf w}_{t-1}(\tilde{\bf x}_{t-1}) + \tilde{\bf m}_t \odot \tilde{\bf h}_t \tag{1}
とする。まず右辺1項目は optical flow に基づく部分で $t-1$ フレームの推定画像 $\tilde{\bf x}_{t-1}$ を optical flow $\tilde{\bf w}_{t-1}$ で推移させることで求める。右辺2項目は optical flow では求まらない ocullusion な部分。両者を mask でわけて計算している。$\odot$ はアダマール積。
ganarotor ネットワークのアーキテクチャは以下。
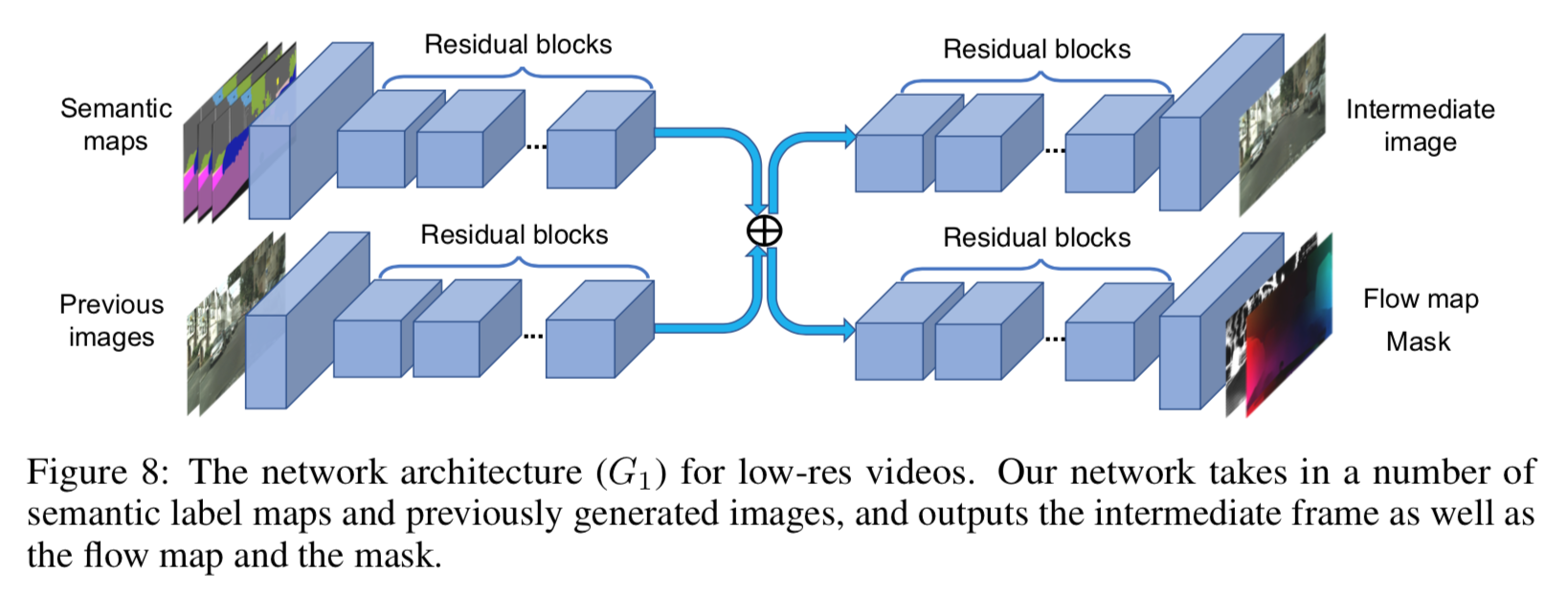
これに先ほどの記号をあてはめるとこんな感じ。
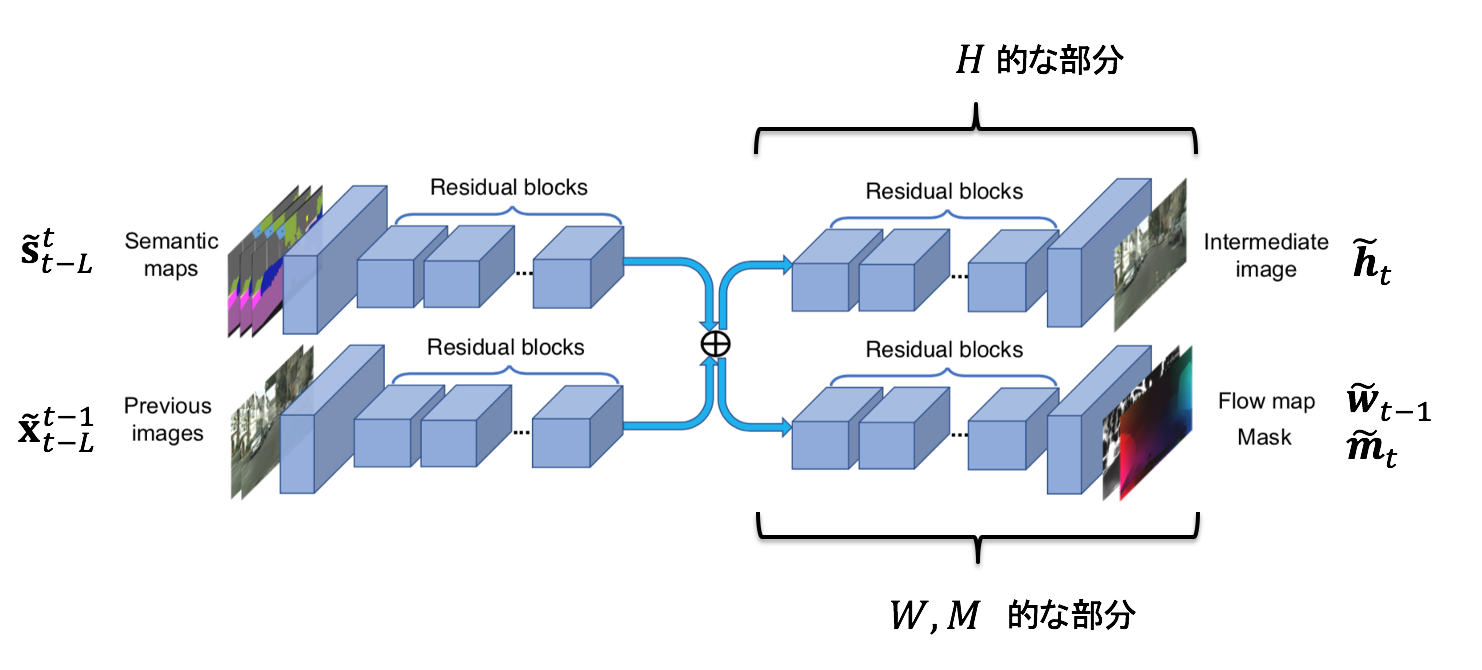
セグメントのシーケンスと生成画像のシーケンスとは分けて特徴量を取ってる。それを add? した後、occulusionな部分を創造するパートと optical flow 、及び mask を推定するパートに分かれる。
前景と後景に分離して計算する
さらに、$(1)$ 式第2項を前景部分(人や車)と後景部分(建物や道路)に分離する。前景部分と後景部分は動きがかなり違うので、これらを分けて推論させるとうまくいくだろう、という発想。
具体的には image hallucination network を前景部分 $\tilde{\bf h}_{t}$ を
- 前景部分・・・$\tilde{\bf h}_{F, t} = H_F (\tilde{\bf s}^t_{t-L})$
- 後景部分・・・$\tilde{\bf h}_{B, t} = H_B (\tilde{\bf x}^{t-1}_{t-L}, \tilde{\bf s}^t_{t-L})$
に分ける。前景部分はセグメンテーションのシーケンスのみから推定する。よって (1)式は前景と後景を分けるマスク ${\bf m}_{B,t}$ を用いて
F(\tilde{\bf x}_{t-L}^{t-1}, {\bf s}_{t-L}^{t}) = ({\bf 1} - \tilde{\bf m}_t ) \odot \tilde{\bf w}_{t-1}(\tilde{\bf x}_{t-1}) + \tilde{\bf m}_t \odot (({\bf 1} - {\bf m}_{B,t}) \odot \tilde{\bf h}_{F,t} + {\bf m}_{B,t} \odot \tilde{\bf h}_{B,t}) \tag{2}
とする。
loss
loss の全体像
loss は3つのパーツの合計。
\min_F ( \max_{D_I} \mathcal{L}_I (F, D_I) + \max_{D_V} \mathcal{L}_V (F, D_V)) + \lambda_W \mathcal{L}_W (F)
画像1枚に対しての adversarial な loss。
上式 $\min$ 内第1項は画像1枚に対する adversarial な loss。
\mathcal{L}_I = E_{\phi_I ({\bf x}_1^T, {\bf s}_1^T}) [\log D_I ({\bf x}_i, {\bf s}_i)] + E_{\phi_I ({\bf x}_1^T, {\bf s}_1^T}) [\log(1- D_I ({\bf x}_i, {\bf s}_i))]
つまり各フレームのセグメンテーション画像に対し、生成した画像がそれらしくなるように学習している。
シーケンシャルな画像に対する adversarial な loss
\mathcal{L}_V = E_{\phi_V ({\bf w}_1^{T-1}, {\bf x}_1^T, {\bf s}_1^T)} [\log D_V ({\bf x}_{i-K}^{i-1}, {\bf w}_{i-K}^{i-2})] + E_{\phi_V ({\bf w}_1^{T-1}, \tilde{\bf x}_1^T, {\bf s}_1^T)} [\log(1- D_V (\tilde{\bf x}_{i-K}^{i-1}, {\bf w}_{i-K}^{i-2}))]
こちらは入力が生成した画像のシーケンスと optical flow のシーケンスになってるところが特徴的。
optical flow に対する loss
optical flow に対する loss は、以下。
\mathcal{L}_W = \frac{1}{T-1} \sum^{T-1}_{t=1} \left( \| \tilde{\bf w}_t - {\bf w}_t \|_1 + \| \tilde{\bf w}_t ({\bf x}_t) - {\bf x}_{t+1} \|_1 \right)
第1項は推定した optical flow と実際の optical flow との loss。
第2項は前フレームの実際の画像を推定した optical flow で変換したものと次フレームの実際の画像との loss。
実験と結果
実装の詳細
- 低解像度で学習して高解像度化する
- discriminator は patchGANのようにpatchごと
- フレームレートを変化させる
- 最適化:Adam
- GAN loss は LSGANのleast-square loss
- 2K画像の場合、8個のtesla v100で10日間学習
データセット
Cityscape等いろいろやってるが、ここではFace video 系のみとりあげる
- FaceForensics dataset・・・854のビデオからなる
スケッチから顔を生成させるタスクの場合、まず顔輪郭から Canny edges を抽出してスケッチとする。
メトリクス
- 人の定性的評価
- Frechet Inception Distance
定性的評価
Cityscape を用いた場合の pix2pixHDとCOVSTとの比較は以下。

人の評価が顕著によくなってる
定性的評価
ここではスケッチから顔生成のタスクのみ取り上げる

まぁ、それっぽいのが生成されてる。
感想
optical flow で推定する部分と完全に創造する部分にわけてたり、あるいは後者は更に前景と後景にわけてたりと、興味深い。
ただDeepFake的に狙ったターゲット(例えばトランプの顔)にするにはconditionを与える等の必要があるね。
またそれに関連して、論文中 discussion にも書かれていたが、対象物体のIDを認識しているわけではないので、車の色が途中で変わったりの難点あり。
あと膨大な学習時間をなんとかしてほしい。