論文まとめ：Precise Detection in Densely Packed Scenes

はじめに

６月に開催される CVPR2019 に accept された以下の論文
[1] E. Goldman, et. al."Precise Detection in Densely Packed Scenes"
のまとめ。

arXivのリンク
https://arxiv.org/abs/1904.00853

既に著者らがコードを公開しています。
https://github.com/eg4000/SKU110K_CVPR19

概要

1. 商品棚のように物が密集して並んでいるシーンで正確にdetectionするモデル
2. 矩形の位置・大きさ、及びそのクラス（確信度）に加えてIoUも推定する
3. 推定したIoUを混合ガウス分布に変換し、オーバーラップしている矩形を取り除く

この図でいくと

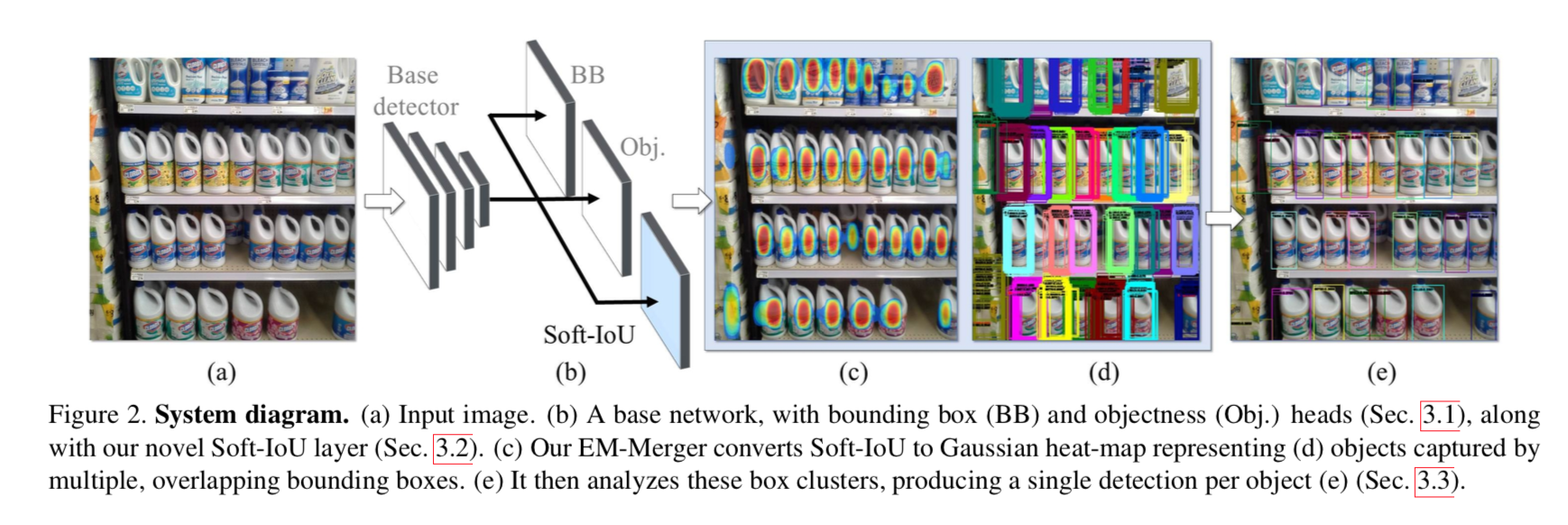[1] figure2より

(a) 棚の密集した商品を

(b) 本モデルに入力すると、

(d) のように冗長な矩形が多数出力されるが、青い Soft-IoU レイヤを用いて

(c) のような分布に変換すると

(e) のような冗長な矩形が除去される

本手法 (Deep IoU detection network) のイメージ

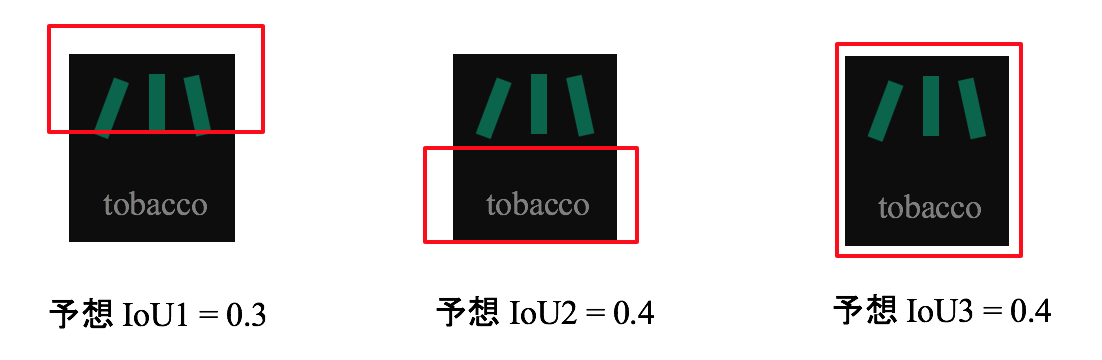
１）従来手法だとこのような物体に対し

２）このように複数の矩形を推定してしまう

３）確信度のようなものを推定しても、いずれの矩形も正確に物体を捉えているので、いずれも1.0となるだろう。よって必要ない矩形の除去には使えない。

４）本モデルでは　予想 IoU も同時に出力する。そうすると、それぞれは物体の一部しか捉えられていない可能性を考慮して低い値になるだろう。

５）これをガウス分布へ変換する。

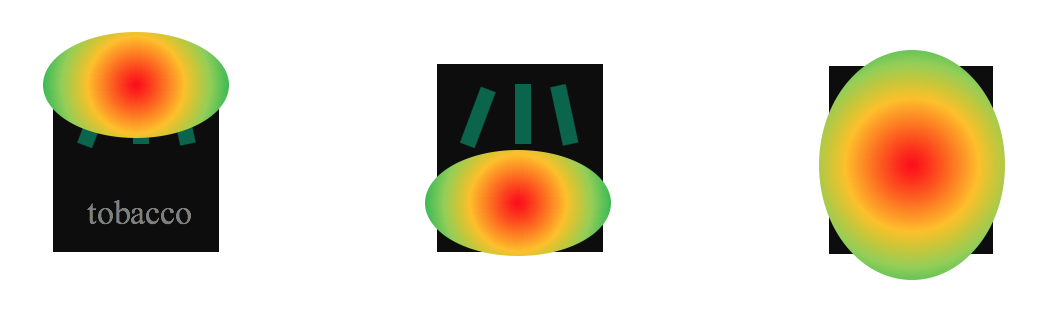
６）さらに予想 IoU を加味して足し合わせる。

７）これを例えば１つの矩形から来たガウス分布になるように最適化させる

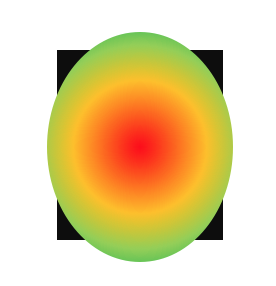
８）これを逆に矩形に戻すと、余計な矩形が除去された１つの正しい矩形になるだろう。

本手法 (Deep IoU detection network) の詳細

全体の流れとしては、

1. soft-IoU layer で IoU を予測する
2. 各矩形をガウス分布へ変換する
3. EM アルゴリズムで少数のガウス分布へ統合する

1. soft-IoU layer で IoU を予測する

ネットワークのこの青い部分・・・soft-IoU layer から

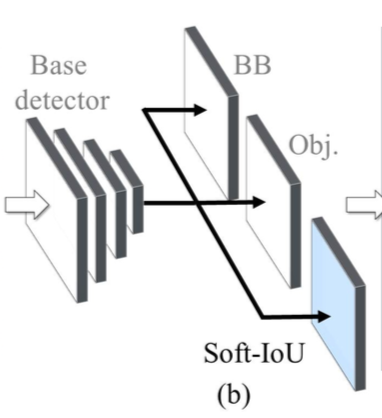
[1]figure2より抜粋

各 bounding box の IoU予測値を出力する。

IoU (intersection over union) は以下。

IoU_i = \frac{Intersection( \hat{b}_i, b_i)}{Union( \hat{b}_i, b_i)}

$b_i$ ：予測 bounding box
$\hat{b}_i$ ：$b_i$ から最も近い ground truth の bounding box

学習時は両者の交差エントロピーを最小化させる。

\mathcal{L}_{sIoU} = -\frac{1}{n} \sum^n_{i=1} [IoU_i \log (c^{iou}_i ) + (1 - IoU_i) \log (1 - c^{iou}_i)]

$c^{iou}_i$ ：$i$ 番目のbounding box に対する $c$ クラスの IoU。
$n$ ：データ数

全体のロスは以下。

\mathcal{L} = \mathcal{L}_{class} + \mathcal{L}_{reg} + \mathcal{L}_{sIoU}

$\mathcal{L}_{class}$ ：物体クラスに関するロスで、交差エントロピーで求める。

$\mathcal{L}_{reg}$ ：矩形の位置・大きさに関するロスで、ユークリッド距離で求める。

2. 各矩形をガウス分布へ変換する

bounding box が N 個あるとして、これを２次元のガウス分布に変換する。

\mathbf{F} = \{ f_i \}^N_{i=1} = \{ \mathcal{N}(\mathbf{p}; \mu_i, \Sigma _i)\}^N_{i=1}

$\mathbf{p} \in \mathbb{R}^2$ ：画像の座標
$\mu_i = (x_i, y_i)$ ：分布の中心・・・bounding boxの中心とする
$\Sigma_i = [(h_i/4)^2, 0; ,0, (w_i/4)^2]$ ：分布の分散共分散行列・・・bounding boxの大きさを反映

これらを全ての bounding box に関して足し合わせて、混合ガウス分布とする。この時、IoUの予測値（を全IoUで正規化したもの）をかけることで重み付けする。

\begin{eqnarray*}
f(\mathbf{p}) &=& \sum^N_{i=1} \alpha_i f_i (\mathbf{p}) \\
\alpha_i &=&\frac{c^{iou}_i}{\sum^{N}_{k=1} c^{iou}_k}  
\end{eqnarray*}

3. EM アルゴリズムで少数のガウス分布へ統合する

最終的に $K << N$ なる K 個の bounding box を推定するとする。

これに対する混合ガウス分布は同様に

\begin{eqnarray*}
g(\mathbf{p}) &=& \sum^K_{j=1} \beta_j g_j (\mathbf{p}) \\
\mathbf{G} = \{ g_j \}^K_{j=1} &=& \{ \mathcal{N}(\mathbf{p}; \mu'_j, \Sigma' _j)\}^K_{j=1} \\
\end{eqnarray*}

とする。

$f$ と $g$ とのKL-divergence を最小化させることで、$g$ を求める。

d(f,g) = \sum^N_{i=1} \alpha_i \min^K_{j=1} KL(f_i \| g_j)

ここで EM アルゴリズムを用いる。

まず E-step。

\pi (i) = \arg \min^K_{j=1} KL(f_i \| g_j) 

次に M-step。

\begin{eqnarray*}
\beta_j &=& \sum_{i \in \pi^{-1} (j)} \alpha_i\\
\mu'_j &=& \frac{1}{\beta_j}\sum_{i \in \pi^{-1} (j)} \alpha_i \mu_i \\
\Sigma'_j &=& \frac{1}{\beta_j}\sum_{i \in \pi^{-1} (j)} \alpha_i (\Sigma_i + (\mu_i - \mu'_j)(\mu_i - \mu'_j)^T)
\end{eqnarray*}

これを $d(f,g) < 1e -10$ まで続けるが、だいたい１０stepで終了するそう。

実験と結果

書きかけ