概要

以下の内容の個人的まとめ。

四元数（クォータニオン）を用いたプロクルステス問題の解法
回転行列の最適補正
その周辺の話題

参考資料

３次元回転に関して丁寧に解説されている本

金谷健一著　「３次元回転　ーパラメータKさんとリー代数による最適化」共立出版

こちらの本は非常に丁寧に書かれているので、ご購入されるとよいと思います。
以下ではこの本のことを回転本といいます。

四元数を用いたプロクルステス問題の解法を示した論文

B.K.P.Horn Closed-form solution of absolute orientation using unit quaternions

1. 四元数（クォータニオン）を用いたプロクルステス問題の解法

1.1 回転行列を用いたプロクルステス問題

剛体の回転を考える。剛体上のNこの観測点に関して、

${\bf a}_\alpha \ \ (\alpha=1, \ldots ,N)$ :回転前の点の座標

${\bf a}_\alpha' \ \ (\alpha=1, \ldots ,N)$ :回転後の点の座標

とする。

図を入れる

回転行列 ${\rm \bf R}$ を用いたプロクルステス問題を考える。

J = \frac{1}{2} \sum^{N}_{\alpha = 1} \| {\bf a}_{\alpha}' - {\bf R}{\bf a}_{\alpha} \|^2 \rightarrow min \tag{1.1.1}

これを展開して

\begin{eqnarray}
J &=& \frac{1}{2} \sum^{N}_{\alpha = 1} \| {\bf a}_{\alpha}' - {\bf R}{\bf a}_{\alpha} \|^2 \tag{1.1.2} \\
&=& \frac{1}{2} \sum^{N}_{\alpha = 1} \| {\bf a}_{\alpha}'\|^2 - \sum^{N}_{\alpha = 1} \langle {\bf R}{\bf a}_\alpha , {\bf a}_{\alpha}' \rangle + \frac{1}{2} \sum^{N}_{\alpha = 1} \| {\bf a}_{\alpha} \|^2  \tag{1.1.3} \\
\end{eqnarray}

１項目と３項目はconstなので J を最小化するには２項目の

K = \sum^{N}_{\alpha = 1} \langle {\bf R}{\bf a}_\alpha , {\bf a}_{\alpha}' \rangle \tag{1.1.4}

を最大化させればいい。

1.2 四元数によるプロクルステス問題の表記

回転行列 ${\bf R}$ は四元数 $q = q_0 + q_1i + q_2j + q_3k$ を用いて

{\bf R} = 
\begin{pmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2 - q_0q_3)            & 2(q_1q_3 + q_0q_2) \\
2(q_2q_1 + q_0q_3)      & q_0^2 - q_1^2 + q_2^2 - q_3^2 & 2(q_2q_3 - q_0q_1) \\
2(q_3q_1 - q_0q_2)      & 2(q_3q_2 + q_0q_1)            & q_0^2-q_1^2-q_2^2+q_3^2 
\end{pmatrix} \tag{1.2.1}

とかけるので、(1.1.4)式 K 内の ${\bf R}{\bf a}_{\alpha}$ は

{\bf a}_{\alpha} =
\begin{pmatrix}
a_{\alpha (1)} \\
a_{\alpha (2)} \\
a_{\alpha (3)}
\end{pmatrix}\tag{1.2.2}

を用いて

\begin{eqnarray}
{\bf R}{\bf a}_{\alpha} &=& \begin{pmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2 - q_0q_3)            & 2(q_1q_3 + q_0q_2) \\
2(q_2q_1 + q_0q_3)      & q_0^2 - q_1^2 + q_2^2 - q_3^2 & 2(q_2q_3 - q_0q_1) \\
2(q_3q_1 - q_0q_2)      & 2(q_3q_2 + q_0q_1)            & q_0^2-q_1^2-q_2^2+q_3^2 
\end{pmatrix} 
\begin{pmatrix}
a_{\alpha (1)} \\
a_{\alpha (2)} \\
a_{\alpha (3)}
\end{pmatrix} \\

&=& 
\begin{pmatrix}
(q_0^2+q_1^2-q_2^2-q_3^2) a_{\alpha (1)}+2(q_1q_2 - q_0q_3)a_{\alpha (2)}+2(q_1q_3 + q_0q_2) a_{\alpha (3)} \\
2(q_2q_1 + q_0q_3) a_{\alpha (1)}+(q_0^2 - q_1^2 + q_2^2 - q_3^2) a_{\alpha (2)} + 2(q_2q_3 - q_0q_1) a_{\alpha (3)} \\
2(q_3q_1 - q_0q_2) a_{\alpha (1)} + 2(q_3q_2 + q_0q_1) a_{\alpha (2)} + (q_0^2-q_1^2-q_2^2+q_3^2 )a_{\alpha (3)}
\end{pmatrix}\tag{1.2.3}
\end{eqnarray}

となるので、$\langle {\bf R}{\bf a}_\alpha , {\bf a}_{\alpha}' \rangle$ は

\begin{eqnarray}
\langle {\bf R}{\bf a}_\alpha , {\bf a}_{\alpha}' \rangle &=& 
\begin{pmatrix}
(q_0^2+q_1^2-q_2^2-q_3^2) a_{\alpha (1)}+2(q_1q_2 - q_0q_3)a_{\alpha (2)}+2(q_1q_3 + q_0q_2) a_{\alpha (3)} \\
2(q_2q_1 + q_0q_3) a_{\alpha (1)}+(q_0^2 - q_1^2 + q_2^2 - q_3^2) a_{\alpha (2)} + 2(q_2q_3 - q_0q_1) a_{\alpha (3)} \\
2(q_3q_1 - q_0q_2) a_{\alpha (1)} + 2(q_3q_2 + q_0q_1) a_{\alpha (2)} + (q_0^2-q_1^2-q_2^2+q_3^2 )a_{\alpha (3)}
\end{pmatrix} \ast 
\begin{pmatrix}
a_{\alpha (1)}' \\
a_{\alpha (2)}' \\
a_{\alpha (3)}'
\end{pmatrix} \\ \tag{1.2.4}

&=& \ \ 

(q_0^2+q_1^2-q_2^2-q_3^2) a_{\alpha (1)}a_{\alpha (1)}'+2(q_1q_2 - q_0q_3)a_{\alpha (2)}a_{\alpha (1)}'+2(q_1q_3 + q_0q_2) a_{\alpha (3)}a_{\alpha (1)}' \\
\ \   &+& 2(q_2q_1 + q_0q_3) a_{\alpha (1)}a_{\alpha (2)}'+(q_0^2 - q_1^2 + q_2^2 - q_3^2) a_{\alpha (2)}a_{\alpha (2)}' + 2(q_2q_3 - q_0q_1) a_{\alpha (3)}a_{\alpha (2)}' \\
\ \  &+& 2(q_3q_1 - q_0q_2) a_{\alpha (1)}a_{\alpha (3)}' + 2(q_3q_2 + q_0q_1) a_{\alpha (2)}a_{\alpha (3)}' + (q_0^2-q_1^2-q_2^2+q_3^2 )a_{\alpha (3)}a_{\alpha (3)}'


\end{eqnarray}

となる。ここで＊は内積。よって (1.1.4) のKは

\begin{eqnarray}
K &=& \sum^{N}_{\alpha = 1} \langle {\bf R}{\bf a}_\alpha , {\bf a}_{\alpha}' \rangle \\
 &=& \sum^{N}_{\alpha = 1} \{
(q_0^2+q_1^2-q_2^2-q_3^2) a_{\alpha (1)}a_{\alpha (1)}'+2(q_1q_2 - q_0q_3)a_{\alpha (2)}a_{\alpha (1)}' \\ &+&  2(q_1q_3 + q_0q_2) a_{\alpha (3)}a_{\alpha (1)}' + 2(q_2q_1 + q_0q_3) a_{\alpha (1)}a_{\alpha (2)}' \\ &+& (q_0^2 - q_1^2 + q_2^2 - q_3^2) a_{\alpha (2)}a_{\alpha (2)}' + 2(q_2q_3 - q_0q_1) a_{\alpha (3)}a_{\alpha (2)}' \\
&+& 2(q_3q_1 - q_0q_2) a_{\alpha (1)}a_{\alpha (3)}' + 2(q_3q_2 + q_0q_1) a_{\alpha (2)}a_{\alpha (3)}' \\ &+& (q_0^2-q_1^2-q_2^2+q_3^2 )a_{\alpha (3)}a_{\alpha (3)}' \}\tag{1.2.5}


\end{eqnarray}

これを ${\bf q}$ に関してまとめたい。よって各 $q_x$ でまとめ直す。

\begin{eqnarray}
K  &=& \sum^{N}_{\alpha = 1} \{
q_0^2 (a_{\alpha (1)}a_{\alpha (1)}' + a_{\alpha (2)}a_{\alpha (2)}' + a_{\alpha (3)}a_{\alpha (3)}) +
q_1^2 (a_{\alpha (1)}a_{\alpha (1)}' - a_{\alpha (2)}a_{\alpha (2)}' - a_{\alpha (3)}a_{\alpha (3)}) \\
&+& q_2^2 (- a_{\alpha (1)}a_{\alpha (1)}' + a_{\alpha (2)}a_{\alpha (2)}' - a_{\alpha (3)}a_{\alpha (3)}) 
+ q_3^2 (- a_{\alpha (1)}a_{\alpha (1)}' - a_{\alpha (2)}a_{\alpha (2)}' + a_{\alpha (3)}a_{\alpha (3)}) \\
&+& 2q_0q_1(a_{\alpha (2)}a_{\alpha (3)}' - a_{\alpha (3)}a_{\alpha (2)}') 
+ 2q_0q_2(-a_{\alpha (1)}a_{\alpha (3)}' + a_{\alpha (3)}a_{\alpha (1)}') \\
&+& 2q_0q_3(a_{\alpha (1)}a_{\alpha (2)}' - a_{\alpha (2)}a_{\alpha (1)}') 
+ 2q_1q_2(a_{\alpha (1)}a_{\alpha (2)} + a_{\alpha (2)}a_{\alpha (1)}') \\
&+& 2q_1q_3(a_{\alpha (1)}a_{\alpha (3)} + a_{\alpha (3)}a_{\alpha (1)})
 + 2q_2q_3(a_{\alpha (2)}a_{\alpha (3)} + a_{\alpha (3)}a_{\alpha (2)})
 \} \tag{1.2.6}
\end{eqnarray}

ごちゃごちゃしてきたので回転本やHornの論文の表記に従って、

N_{ij} = \sum_{\alpha=1}^{N} a_{\alpha (i)}a_{\alpha (j)} \tag{1.2.7}

とすると、

\begin{eqnarray}
K  &=&  
q_0^2 (N_{1,2} + N_{2,2} + N_{3,3}) + q_1^2 (N_{1,1} - N_{2,2} - N_{3,3}) \\
&+& q_2^2 (- N_{1,1} + N_{2,2} - N_{3,3}) + q_3^2 (- N_{1,1} - N_{2,2} + N_{3,3}) \\
&+& 2q_0q_1(N_{2,3} - N_{3,2}) + 2q_0q_2(-N_{1,3} + N_{3,1}) \\
&+& 2q_0q_3(N_{1,2} - N_{2,1}) + 2q_1q_2(N_{1,2} + N_{2,1}) \\
&+& 2q_1q_3(N_{1,3} + N_{3,1}) + 2q_2q_3(N_{2,3} + N_{3,2}) \tag{1.2.8}
\end{eqnarray}

そうすると、$q_x$ に関して二次式となっているので、これのまとめ方として

{\bf q}{\bf q}^{\top}{\bf \tilde{N}} \tag{1.2.9}

とか

\langle {\bf q}, {\bf \tilde{N}}{\bf q} \rangle \tag{1.2.10}

といったものが想像できる。

後者で考えると、$q^2_x$ の係数が $\tilde{N}$ の対角成分に並ぶので

\tilde{N} =

\begin{pmatrix}
N_{1,2} + N_{2,2} + N_{3,3} & \cdots & \cdots & \cdots \\
\cdots & N_{1,2} - N_{2,2} - N_{3,3} & \cdots & \cdots \\
\cdots & \cdots & - N_{1,2} + N_{2,2} - N_{3,3} & \cdots \\
\cdots & \cdots & \cdots & -N_{1,2} - N_{2,2} + N_{3,3}
\end{pmatrix} \tag{1.2.11}

となればいいだろう。

それ以外の成分に関しては、例えば $q_0q_1$ の係数はこの行列の(0, 1)成分と(1, 0)成分に対応するので、

\tilde{N} =

\begin{pmatrix}
\cdots & N_{2,3} - N_{3,2} & \cdots & \cdots \\
N_{2,3} - N_{3,2} & \cdots & \cdots & \cdots \\
\cdots & \cdots & \cdots & \cdots \\
\cdots & \cdots & \cdots & \cdots
\end{pmatrix} \tag{1.2.12}

とすれば足して２倍となってちょうどいい。そうすると、(1.2.8)式の $q_iq_j \left( i\neq j \right)$ となる６つの項は $\tilde{N}$ の非対角成分と対応する。

よって、求める行列は

\tilde{N} =
\begin{pmatrix}
N_{1,2} + N_{2,2} + N_{3,3} & N_{2,3} - N_{3,2} & -N_{1,3} + N_{3,1} & N_{1,2} - N_{2,1} \\
N_{2,3} - N_{3,2} & N_{1,1} - N_{2,2} - N_{3,3} & N_{1,2} + N_{2,1} & N_{1,3} + N_{3,1} \\
-N_{1,3} + N_{3,1} &  N_{1,2} + N_{2,1} & - N_{1,1} + N_{2,2} - N_{3,3} & N_{2,3} + N_{3,2} \\
N_{1,2} - N_{2,1} & N_{1,3} + N_{3,1} & N_{2,3} + N_{3,2} & -N_{1,1} - N_{2,2} + N_{3,3}
\end{pmatrix} \tag{1.2.13}

とわかる。これにより求める最大化問題は

K = \langle {\bf q}, {\bf \tilde{N}}{\bf q} \rangle \rightarrow max \tag{1.2.14}

となる。

${\bf q}$ は４次元だが、わかりやすく３次元で考えてみる。

この図のように ${\bf q}$ ベクトルがあって、それが一次変換${\bf \tilde{N}}$ によって回転・伸縮させられる。

一次変換${\bf \tilde{N}}$ はconstで、 ${\bf q}$ ベクトルは任意に選択できる。ただし、 ${\bf q}$ は四元数なのでノルムは１である。

このとき、どのような ${\bf q}$ ベクトルが内積 $ \langle {\bf q}, {\bf \tilde{N}}{\bf q} \rangle$ を最大化させられるだろうか。

考えられる１つは、以下の図のように $\tilde{N}$ によって向きが変わらないもの。

そうすると両者の $\cos \theta$ が最大なので、筋がよさそう。その場合、${\bf q}$ は $\tilde{N}$ の固有ベクトル。

さらに、同じ向きの中ではより大きさが増大する方がよい。

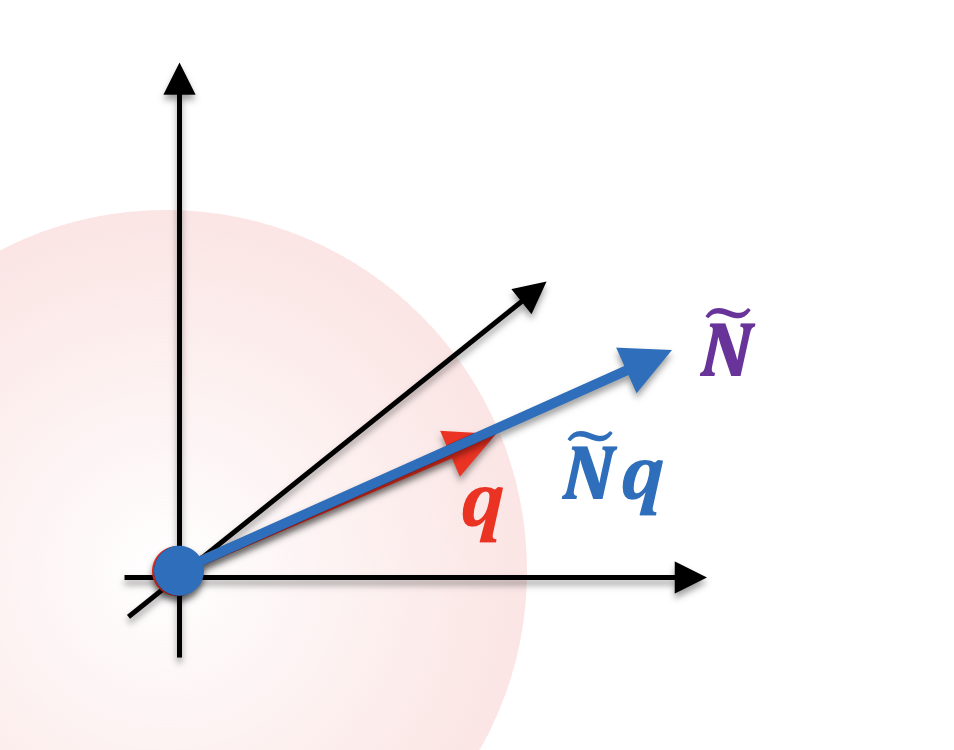
なので、結局、${\bf q}$ は $\tilde{N}$ の固有ベクトルの中で最大固有値に対応するものがよさげ。 -> 証明は？

回転行列の最適補正

プロクルステス問題を解いて回転行列を得たとしても、誤差のためにそれらが正しい回転行列・・つまりその列ベクトルが正規直交系をなしている・・・とは限らない。

今、

${\bf \hat{R}}$ : 観測点から推定した回転行列

${\bf R}$ : 補正後の（烈ベクトルをより正規直交系に近づけた？）回転行列

とする。

やりたいことは、できるだけ値を変えずに ${\bf \hat{R}}$ を ${\bf R}$ に変換すること。そこで ${\bf R}$ と ${\bf \hat{R}}$ との距離の測り方が重要となるが、ここでは回転本に従って以下のフロベニウスノルムを用いる。

\| {\bf A} \|_F = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} A_{ij}^2} \tag{2.1}

よって、問題の定式化をすると

\newcommand{\argmin}{\mathop{\rm arg~min}\limits}

{\bf R} = \argmin_{R} \| {\bf R} - \hat{\bf R} \|_F^2 \tag{2.2}

という感じか。後の計算のため２乗とした。具体的にはフロベニウスノルムの２乗がtransposeとの積のトレースとなることを用いる。

\| {\bf A} \|_F^2 = {\rm tr} ({\bf A}{\bf A}^\top ) = {\rm tr} ({\bf A}^\top {\bf A} )

そうすると(2.2)式は

\begin{eqnarray}

\| {\bf R} - \hat{\bf R} \|_F^2 &=& {\rm tr}(({\bf R} - \hat{\bf R})({\bf R} - \hat{\bf R})^{\top}) \tag{2.3} \\
&=& {\rm tr}(({\bf R} - \hat{\bf R})({\bf R}^{\top} - \hat{\bf R}^{\top})) \tag{2.4} \\
&=& {\rm tr}({\bf R}{\bf R}^\top - {\bf R}\hat{\bf R}^\top - \hat{\bf R}{\bf R}^{\top} + \hat{\bf R} \hat{\bf R}^\top) \tag{2.5} \\
&=& {\rm tr}({\bf R}{\bf R}^\top) - {\rm tr}({\bf R}\hat{\bf R}^\top) - {\rm tr}(\hat{\bf R}{\bf R}^{\top}) + {\rm tr}(\hat{\bf R} \hat{\bf R}^\top) \tag{2.6} \\
&=& {\rm tr}{\bf I} - {\rm tr}({\bf R}\hat{\bf R}^\top) - {\rm tr}({\bf R}\hat{\bf R}^\top)^\top + {\rm tr}(\hat{\bf R} \hat{\bf R}^\top) \tag{2.7} \\
&=& 3 - 2{\rm tr}({\bf R}\hat{\bf R}^\top) + \|\hat{\bf R}\|_F^2 \tag{2.8} \\
\end{eqnarray}

となる。

(2.3)式から(2.4)式へは引いてからtransposeしてもtransposeして引いても同じとなる性質、(2.5)式から(2.6)式へは足したり引いたりしてtraceを求めてもtrace求めて足したり引いても同じとなる性質、(2.7)式から(2.8)式へはtransposeしてもtraceは変わらない性質及びフロベニウスノルムの２乗がtransposeとの積のtraceとなる性質をそれぞれ用いた。

(2.8)式において、３項目はconst。よって(2.8)式を最小化することは２項目を最大化させること。つまり求める ${\bf R}$ は

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}

{\bf R} = \argmax_{R} {\rm tr}({\bf R}  \hat{\bf R}^\top)  \tag{2.9}

これは $\hat{\bf R}$ の特異値分解を

\hat{\bf R} = {\bf U \Sigma V}^\top

として

{\bf R} = {\bf U}
\begin{pmatrix}
1 & 0 &  0 \\
0 & 1 & 0 \\
0 &0 & | {\bf UV} |
\end{pmatrix}
{\bf V}^\top

となる。（途中過程は回転本第四章の３など参照されたし）

個人的な疑問

前節で書いた四元数を用いてプロクルステス問題を解いた場合、得られる四元数のノルムが１となるよう各要素 $q_0, q_1, q_2, q_3$ を補正したのではダメなのか？それを求めて(1.1.2)式で回転行列に変換した方が早そうだが。。。