はじめに
今更ながらOpenPoseとして知られる以下の論文をまとめてみる。
論文:[1] Z. Cao, et. al. "Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields"
https://arxiv.org/abs/1611.08050
既にslideshareにもまとめがあがってる。
松尾研の大野氏:
https://www.slideshare.net/ShunsukeOno/realtime-multiperson-2d-pose-estimation-using-part-affinity-fields-78988208
概要
- 下図のように2Dにおいて人の姿勢推定を行うモデル
- 関節の位置を推定しつつ、PAFs(part affinity fields:後述)を用いてaffinityの推定を行う
- ボトムアップ方式
- リアルタイムな検出を行いつつ高い精度を達成した
 [1]figure 1より
[1]figure 1より
アーキテクチャ
全体図
全体的なアーキテクチャは以下の図([1]のFigure 3より)
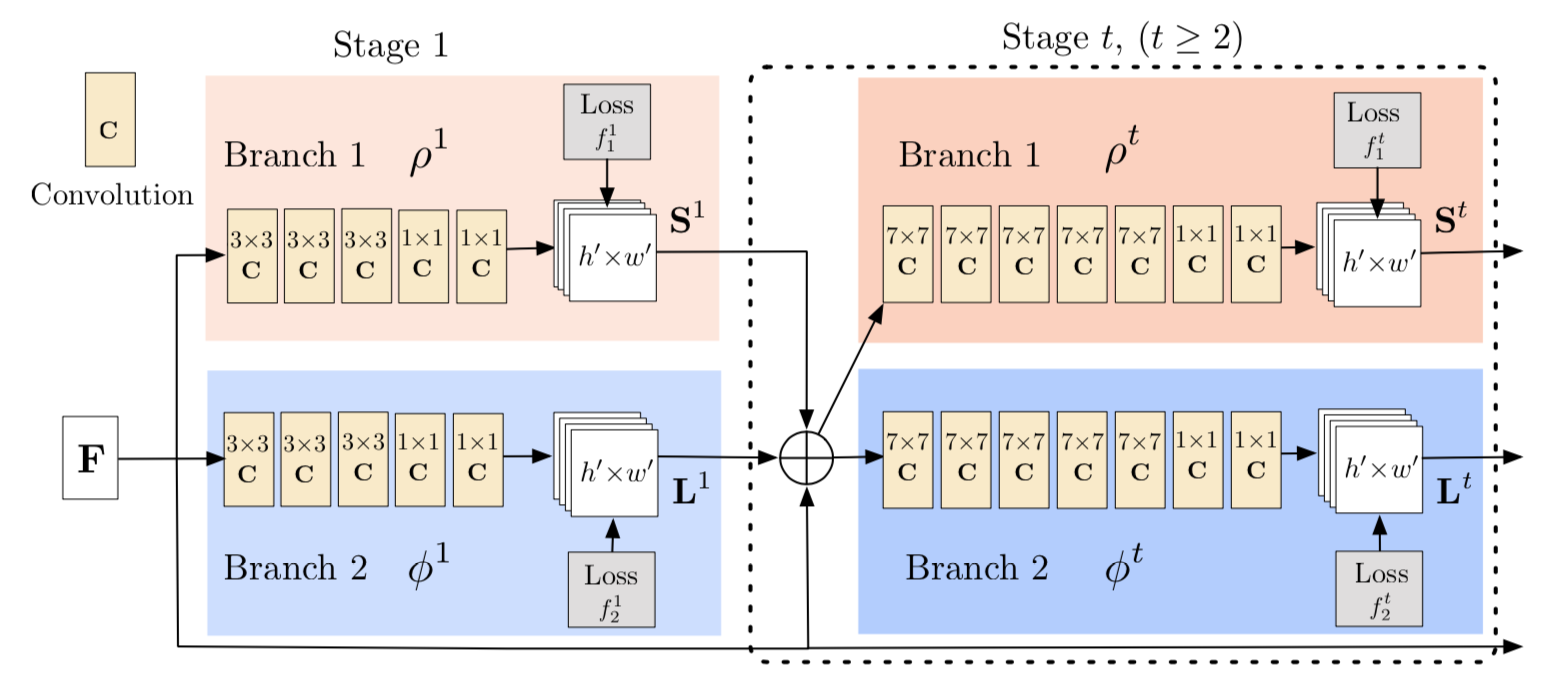
まず複数のstageに分かれている
各stageでは2つのbranchがあって、一方で関節位置 $S^t$ 、もう一方で骨格の向き $L^t$ を推定する。
Branch 1 (confidence map)
上側のBranch 1 では各関節位置 $S = (S_1, S_2, \cdots , S_J )$ の確信度マップを出力する。J は関節で、Jチャンネル存在する。
t stage目の出力は前のstageの出力 $S^{t-1}$ 、 $L^{t-1}$およびstage1への入力値 $F$ を複数回畳み込んだもの。
\begin{eqnarray}
S^t &=& \rho^t (F, S^{t-1} , L^{t-1}) , \forall t \ge 2,
\end{eqnarray}
各 stageごとに目標値confidence mapとの2乗誤差で loss を求め、それを足し合わせる。
F^t_L = \sum^J_{c=1} \sum_p W(p) \cdot \parallel S^t_j(p) - S^*_j(p) \parallel_2^2
confidence map の作り方
ここで問題は confidence map の目標値 $S^*$ をどうやって作るか。
画像中のk番目の人の関節jの confidence map の目標値を $S^*_{j,k}$ とする。
$x_{j,k} \in \mathbb{R}^2$ をk番目の人の関節jのground truthとする。
$p \in \mathbb{R}^2$ ピクセルの $S^*_{j,k}$ は
S^*_{j,k}(p) = exp \left( -\frac{\parallel p - x_{k,j} \parallel ^2_2}{\sigma ^2} \right)
とする。つまりground truthのピクセル $x_{k,j}$ を中心として分散σのgauss分布をかける感じ。
最終的な confidence map はk 人に渡って足し合わせる。この時、各人の最大値とする。
S^*_{j}(p) = \max_k S^*_{j,k} (p)
推論の段階では non-maximum supressionを使う。
Branch 2(Part Affinity Fields)
関節位置がわかっただけでは、骨格は作れない。画像中に複数の人がいる場合、どの右肩とどの右ひじを対応させるべきか定まらない。
そこでPart Affinity Fieldsという考え方を使う。例えばこの図
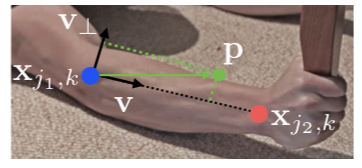 [1]の図より
[1]の図より
において関節 $x_{j_1, k}$ と $x_{j_2, k}$ がある。この両者を結びつけるものがPart Affinity Fields。それはこの図
 [1]figure 1より
[1]figure 1より
のように関節と関節の間の領域をベクトル場にする。具体的には関節と関節の間をlimb $c$ としたときに part affinity vector field $L^*_{c,k}$ は
L^*_{c,k}(\bf{p}) = \begin{cases}
v & if\: \bf{p} \: \rm on \: limb \: c,k \\
0 & otherwise
\end{cases}
ここで $v$ は
v = \frac{(x_{j_2,k} - x_{j_1,k})}{\parallel x_{j_2,k} - x_{j_1,k} \parallel_2}
と関節 $x_{j_1,k}$ から関節 $x_{j_2,k}$ 方向への単位ベクトルとなる。
つまり対象のピクセル $\bf{p}$ が四肢(limb)の領域なら $v$ 、そうでないなら 0 とあする。
また四肢(limb)の領域かどうかは以下で定める。
0 \leq \bf{v} \cdot (p - x_{j_1, k}) \leq \rm and \: |\bf{v}_{\perp} \cdot (\bf{p} - x_{j_1, k}) | \leq \sigma_l
つまり、関節 $x_{j_1,k}$ と関節 $x_{j_2,k}$ の間にあって、垂直方向にσの範囲に入ってるものを $\bf{p}$ とする。
PAFsのground truthに関しては、confidence mapと違って全ての人にわたった平均で求める。
\bf L_{\rm c}^* (\bf p \rm ) = \frac{1}{n_c (\bf{p} \rm )} \sum_k \bf L_{ \rm c,k}^* \rm (\bf p \rm )
$n_c (\bf p \rm)$ は値が0とならない人。
推論する段階では、このPAFsのベクトル向きに沿って線積分すればいい。
つまり候補の関節位置が $\bf d_{\rm j_1} $ 、$\bf d_{\rm j_2} $ であったとして、予測されたPAFsを $\bf L_{\rm c}$ とすると
E = \int^{u=1}_{u=0} \bf{L}_{\rm c}\rm (\bf{p} \rm (u)) \cdot \frac{(\bf{d}_{\rm j_2} \rm - \bf{d}_{\rm j_1} \rm)}{\parallel \bf{d}_{\rm j_2} \rm - \bf{d}_{\rm j_1} \rm \parallel_2}du
$\bf p \rm (u)$ は
\bf{p} \rm (u) = (1-u)\bf{d \rm}_{\rm j_1}\rm + u \bf d \rm _{j_2}
多人数いるときの骨格の決定法
関節の候補を
\mathcal{D}_\mathcal{J} = \{ \bf{d}^{\rm m}_{\rm j} \rm : for \: j \in \{ 1 \cdots J \}, \: m \in \{ 1 \cdots N_j \} \}
とする。 $\bf{d}^{\rm m}_{\rm j} \in \mathbb{R}^2$ は関節jのm番目候補。
2つの関節候補が接続するか否かは
z^{m, n}_{j_1, j_2} \in \{0,1 \}
で表す。
全ての関節候補の組み合わせは
\mathcal{Z} = \{ z^{m, n}_{j_1, j_2} \: : \: for \: j_1, j_2 \in \{ 1 \cdots J \}, m \in \{1 \cdots N_{j_1} \}, \: n \in \{1 \cdots N_{j_2} \} \}
とする。
limb $c$ に対する関節の組み合わせは以下のmaximum weight で求める。
\begin{eqnarray}
\max_{Z_c} &=& \max_{Z_c} \sum_{m \in \mathcal{D}_{j_1}} \sum_{n \in \mathcal{D}_{j_2}} E_{mn} \cdot z^{m, n}_{j_1, j_2} \\
s.t. && \forall m \in \mathcal{D}_{j_1}, \sum_{n \in \mathcal{D}_{j_2}} z^{m, n}_{j_1, j_2} \leq 1 \\
s.t. && \forall m \in \mathcal{D}_{j_2}, \sum_{n \in \mathcal{D}_{j_1}} z^{m, n}_{j_1, j_2} \leq 1 \\
\end{eqnarray}
実験と結果
以下2つのデータセットで実験を行なった。
- MPⅡ human multi-person dataset
- COCO 2016 keypoints challenge dataset
いずれにおいてもstate-of-the-artな手法を上回った。
MPⅡ human multi-person dataset を用いた結果
MPⅡのtest dataでmAP等を他のstate-of-the-artsな手法と比較した結果が以下。
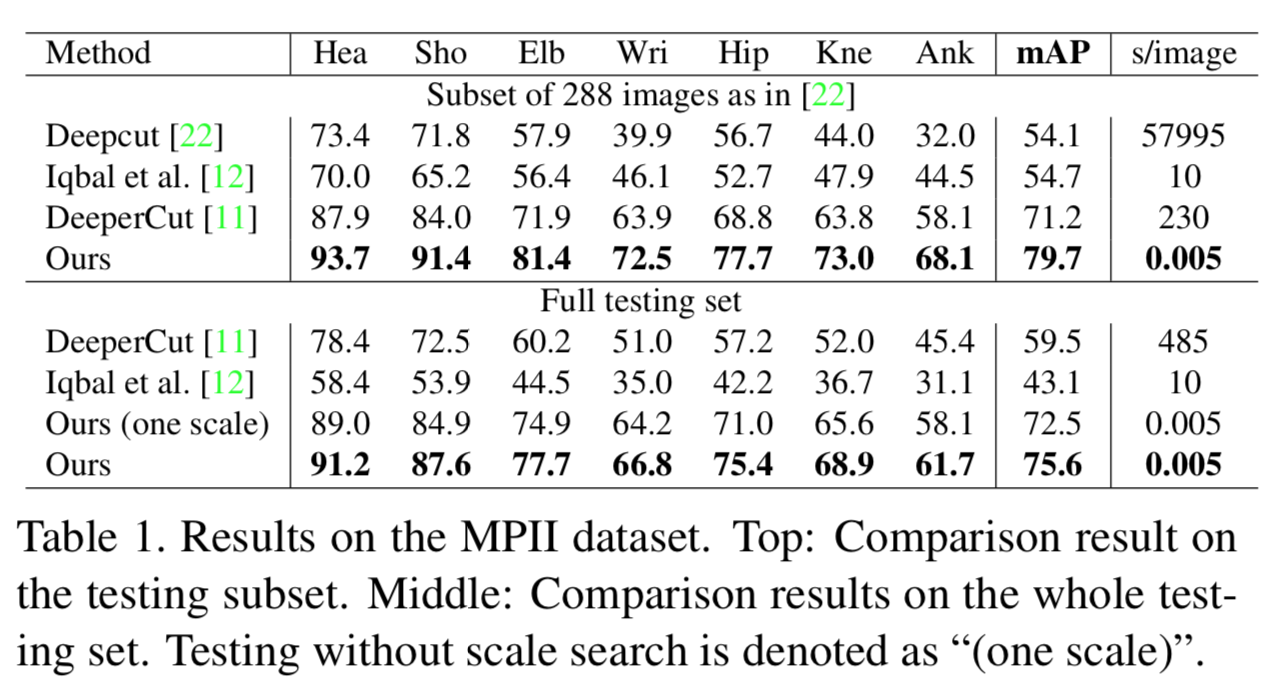
他の手法を大きく上回っている。
次に ablation analysis。下図の左はPCKH-0.5でMAPを比較したもの。
PAFを用いた手法が従来のmidpointよりも優れている。
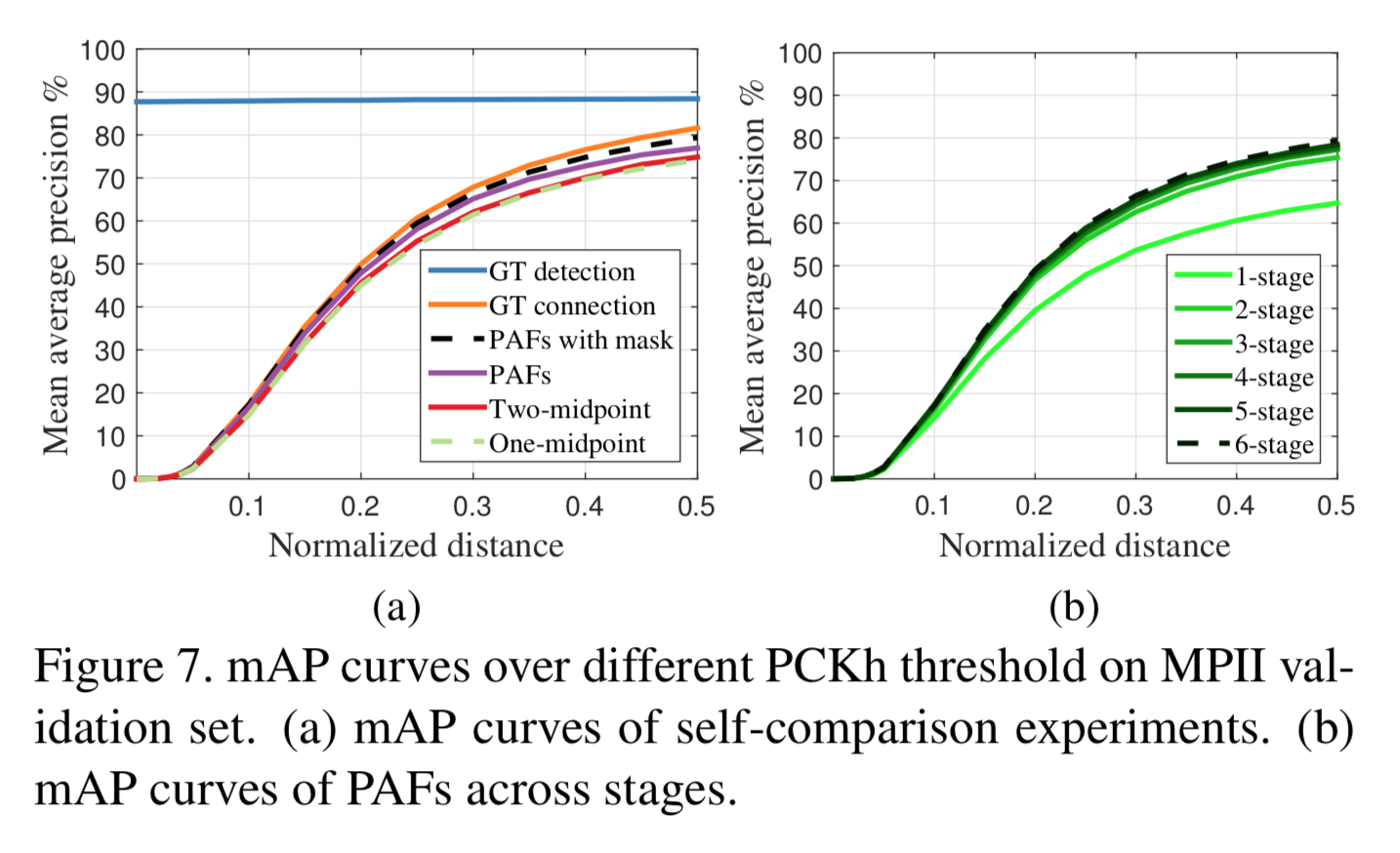
右側はstageの個数を変えてMAPを見たもの。stageが増えるに従って上昇している。
COCO dataを用いた学習結果
以下の図はCOCO 2016 keypoints challenge datasetのtest dataを用いた他の手法とのMAPの比較。
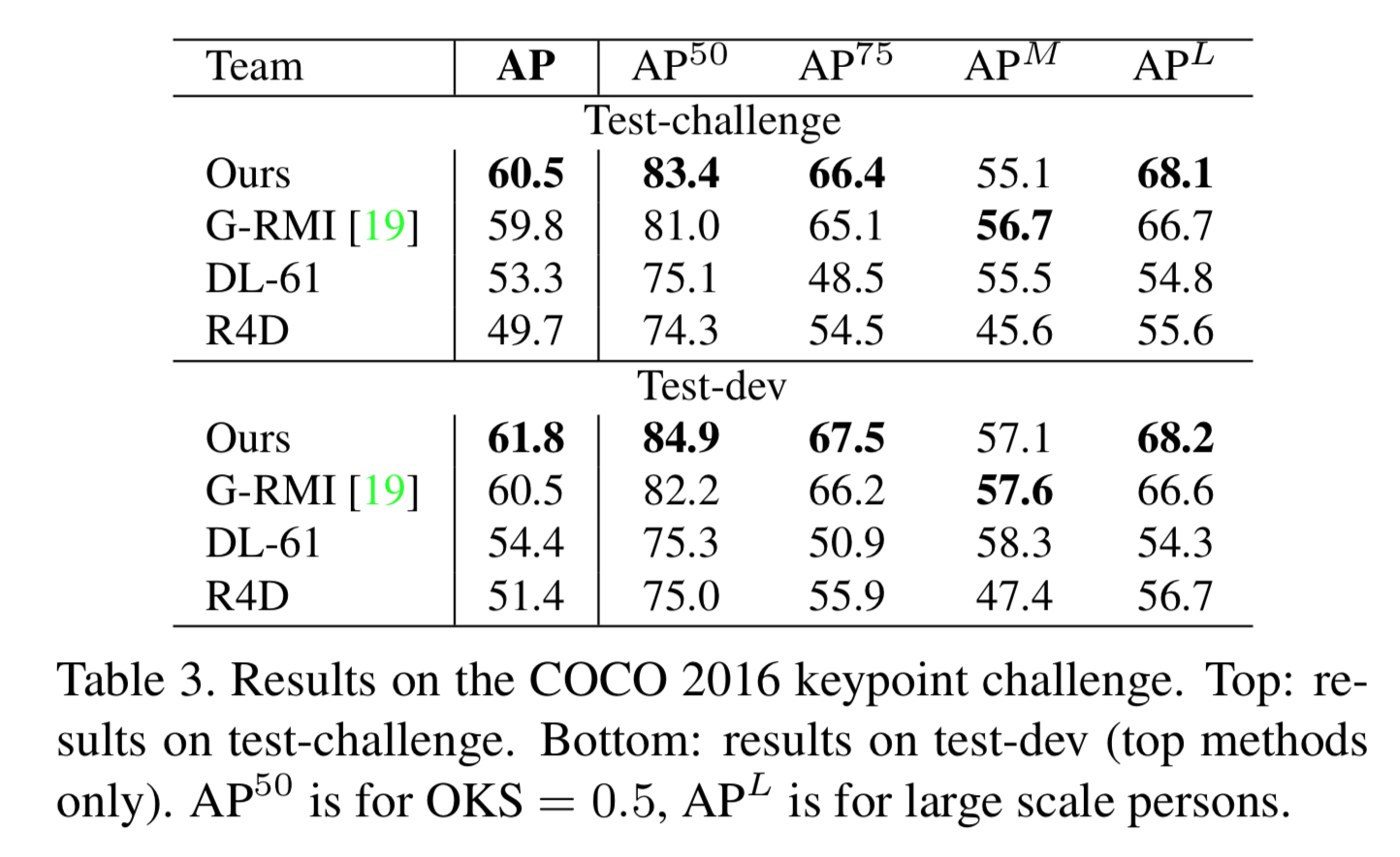
概ね勝ってるが、G-RMI(Towards Accurate Multi-person Pose Estimation in the Wild)に負けてる。
[2]G-RMI(G. Papandreou, et. al. "Towards Accurate Multi-person Pose Estimation in the Wild")
G-MRIは人をdetectionして領域を切り取り、それをrescaleして骨格推定に投げる手法。(下図参照)
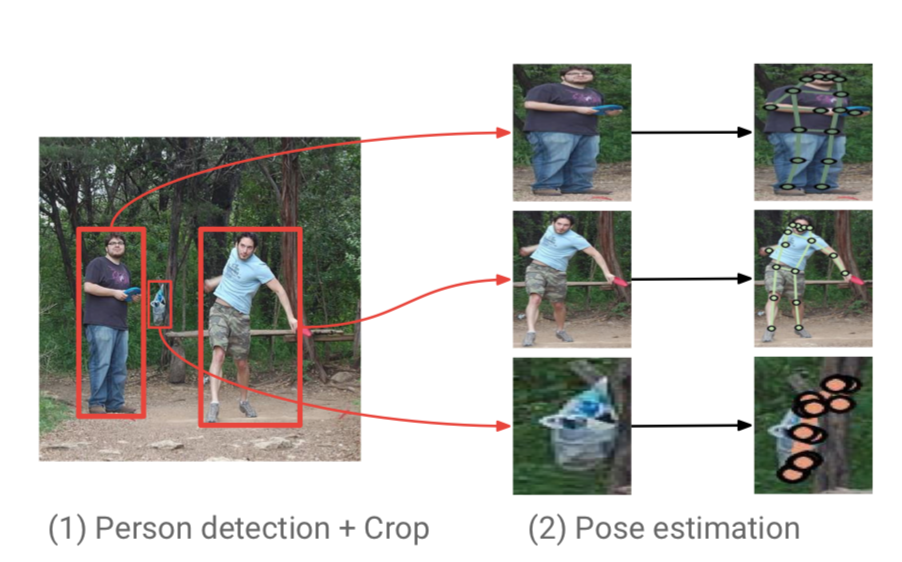 [2]のFigure 1より
[2]のFigure 1より
このような手法は人の領域がrescaleされて大きい情報として扱われるので、その点有利なのか?
演算時間の比較
書きかけ