はじめに
CVPR2019(oral)に accept された以下の論文
[1] Y. Raaj, et. al, "Efficient Online Multi-Person 2D Pose Tracking with Recurrent Spatio-Temporal Affinity Fields"
のまとめ
現状(2019/4/28)ではコードは見当たらず
概要
- 2D画像から骨格のトラッキングをするモデル
- 多数の人に対して同時に、かつリアルタイムで推論できる
- Spatio-Temporal Affinity Fields (STAF)を用いて骨格の推定を行う
出力例

例えば1番上のアメフトの例では、人が重なったり密集したりしているが、各人にP20のようなIDがふられている。左から右へシーンが移動してもIDはおおよそお一致している。
場の定義
3つの要素が登場する。それぞれkeypoints, PAFs(part affinity fields), TAFs(temporal affinity fields)。2番目と3番目を合わせて STAFs(spatio-temporal affinity fields)ともいう。
keypoints
右肩、左肘、などの関節等の位置。本モデルではこの図
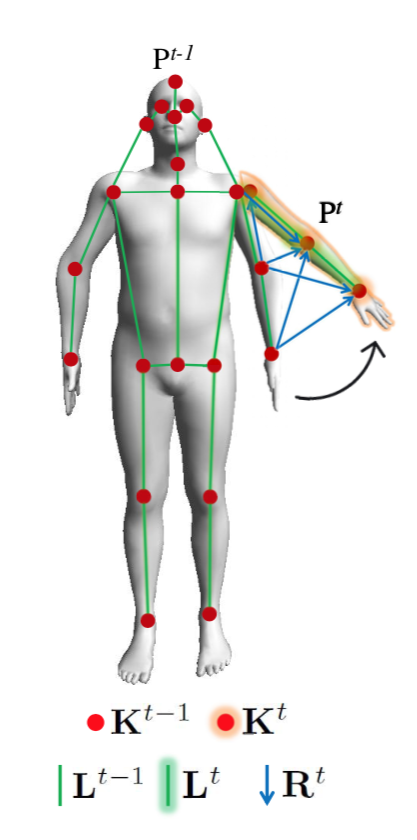
[1]Figure1より抜粋
の赤い点であり、21個ある。また時間によって位置が変化するので、$t$ 時のkeypoints $K$ における値は $K^t_k$ 。
PAFs(part affinity fields)
あるkeypoint $K^t_k$ から隣のkeypoint $K^t_{k'}$ へのlimb。$\Omega(\cdot) $ を単位ベクトルとして、PAFsは
L^t_{k \to k'} := \Omega (K^t_k, K^t_{k'})
となる。
TAFs(temporal affinity fields)
$t-1$ 時のフレームにおけるある keypoint $K^t_k$ から $t$ 時のフレームにおけるkeypoint $K^t_{k'}$ への単位ベクトル。ベクトルの始点と終点は同じkeypointの場合と、異なる場合がある。
R^t_{k \to k'} := \Omega (K^{t-1}_k, K^t_{k'})
モデルのしくみ
全体像は以下の図。
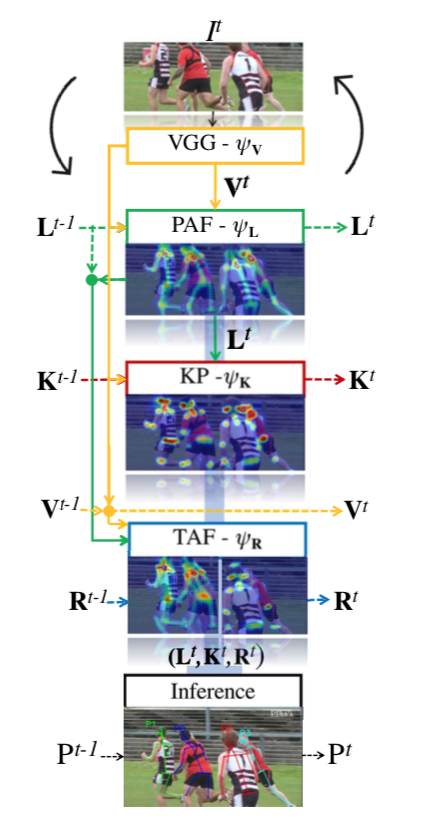
本論文では3種類のモデルを提示している。
以下では
$\psi_V$ :VGG-net・・・最初に特徴量を抽出する
$\psi_L$ :PAFsのモデルでCNN。
$\psi_K$ :keypointsのモデルでCNN。
$\psi_R$ :TAFsのモデルでCNN。
model 1
1)フレーム $t$ における画像 $I^t$ をVGG-net( $\psi_V$ )に入力し、特徴量 $V^t$ を得る。
V^t = \psi_V (I^t)
2)フレーム $t$ におけるPAFsは、フレーム $t$ におけるVGG特徴量、及びフレーム $t-1$ まで $q-1$ 回再帰したPAFsの出力から求める。
L^t = \psi_L (V^t, \psi_L^{q-1} (\cdot))
3)フレーム $t$ におけるkeypointsは、フレーム $t$ におけるVGG特徴量、フレーム $t$ まで $q$ 回再帰したPAFsの出力、及びフレーム $t-1$ まで $q-1$ 回再帰したkeypointsから求める。
K^t = \psi_K (V^t, \psi_L^{q} (\cdot)), \psi^{q-1}_K (\cdot))
4) フレーム $t$ におけるTAFsは、フレーム $t-1$ におけるVGG特徴量、フレーム $t$ におけるVGG特徴量、フレーム $t-1$ におけるPAFs、フレーム $t$ におけるPAFs、フレーム $t-1$ におけるTAFsから求める。
R^t = \psi_R (V^{t-1}, V^t, L^{t-1}, L^t, R^{t-1})
再帰回数 $q$ は5を用いる。
このモデルは精度がいいが、推論の速度が遅い。
model 2
そこで $q$ 回の再帰回数を1回に減らして model 2 とする。
\begin{eqnarray*}
L^t &=& \psi_L (V^t, L^{t-1})\\
K^t &=& \psi_K (V^t, L^{t}, K^{t-1}) \\
R^t &=& \psi_R (V^{t-1}, V^t, L^{t-1}, L^t, R^{t-1})
\end{eqnarray*}
1フレームの情報のみを再利用するが、精度はそれほど落ちないそう。推論速度は上昇。
model 3
model 3 では PAFs(part affinity fields)とTAFs(temporal affininty fields)とを同じCNNとする。
\begin{eqnarray*}
[L^t, R^t] &=& \psi_{[L,R]} (V^{t-1}, V^t, [L, R]^{t-1})\\
K^t &=& \psi_K (V^t, L^{t}, K^{t-1}) \\
\end{eqnarray*}
推論速度は最もよいが、学習が難しい。
STAFs のトポロジー
モデルは3種類だが、それとは別にSTAFsの取り方も3種類考え、検証する。

この図では赤い点がkeypoints、緑の線がPAFs、青い線がTAFs。
タイプ I
Figure 3 の(a)のように同じkeypointsの足跡をTAFsとする。
タイプ Ⅱ
Figure 3 の(b)のように隣のkeypointsを結んでTAFsとする。
タイプ Ⅲ
Figure 3 の(c)のようにPAFsを用いず、同じ、あるいは隣のkeypointsとの足跡を結んだTAFsのみを用いる。(keypointsの数も増やす)
学習方法
事前学習
トラッキングの学習をする前に、1枚1枚のimageで事前学習する。以下用いるデータセット。
- COCO dataset
- MPⅡ dataset
- Posetrack dataset
本学習
次に上記 dataset の video mode で本学習する。
骨格とそのトラッキングの推定方法
以下の手順で骨格形成とトラッキングを行う。
1)PAF及びTAFのweight算出
まず最初に、neural network から推定した PAF $\bar{L}^t$ から、全てのkeypointsのペア $\bar{L}^t_{k \to k'}$ に対する重みを以下で求める。
\begin{eqnarray}
\omega (\bar{K}^t_{k}, \bar{K}^t_{k'})\\
\end{eqnarray}
$\omega$ は2つのkeypoint間のPAFベクトルの平均値と $\bar{K}^t_{k}$ から $\bar{K}^t_{k'}$ への単位ベクトルとの内積。
同様に TAF $\bar{R}^t$ から、全てのkeypointsのペアに対して $\bar{R}^t_{k \to k'}$ に対する重みを以下で計算する。
\begin{eqnarray}
\omega (\bar{K}^{t-1}_{k}, \bar{K}^t_{k'})\\
\end{eqnarray}
2)骨格の仮形成
keypoint と keypoint の weight を小さい順に並べた上で、以下の手順で小さい順に骨格を形成する。
- 両方のkeypoint B, C が他のどのkeypointとも繋がってないなら、そのweightを割り当てる。
- 片方のkeypoint B( or C) に対して既に別の C' (or B') との weight が割り当てられているなら、それに加えて B, C の weight を割り当てる
- 既に両方の keypoint B, C に対するペアに対して weight が存在するなら、値を更新する
- 既に両方の keypoint B, C 対してそれぞれペア A, 及び D とのweightが存在するなら、それらにマージさせて B, C ペアの weight を割り当てる
この処理の後、前フレームで $id=n$ と最も繋がっている 骨格群に対して $id=n$ を割り振る。
3)骨格の確定
この段階では以下の図の $A-B$ 間と $A-E$ 間のように複数の候補が存在する。

この図左側では $t-1$ フレームにおける人1の骨格 $P^{t-1,1}$ と人2の骨格 $p^{t-1, 2}$ とが赤い点と線で表されていて、$t$ フレームにおける人1の骨格と人2の骨格の候補が緑の点と線で表されている。(図中の $\bar{R}^t$ と $\bar{L}^t$ は間違って逆になってる?)
$t$ フレームにおける人2の keypoint A が B と繋がるか、E と繋がるかは以下の値の大きい方を選択する事で決定する。
\bar{L}^{t,n}_{k \to k'} = (1 - \alpha) \times \omega (\bar{K}^{t-1, n}_{k}, \bar{K}^{t, n}_{k'}) + \alpha \times \omega (\bar{K}^{t, n}_{k}, \bar{K}^{t, n}_{k'})
右辺第1項は $\bar{K}^{t-1, n}_{k}$ と $\bar{K}^{t, n}_{k'}$ とのTAFのweightで、第2項は $\bar{K}^{t, n}_{k}$ と $\bar{K}^{t, n}_{k'}$ とのPAFのweightである。
ここからは想定だが・・・・
例えば図中 $A \to B$ のスコア $\bar{L}^{t,1}_{A \to B}$ は
\bar{L}^{t,1}_{A \to B} = (1 - \alpha) \times \omega (\bar{K}^{t-1, 1}_{B}, \bar{K}^{t, 1}_{C}) + \alpha \times \omega (\bar{K}^{t, 1}_{A}, \bar{K}^{t, 1}_{B})
となり、一方 $A \to E$ のスコア $\bar{L}^{t,1}_{A \to E}$ は
\bar{L}^{t,1}_{A \to E} = (1 - \alpha) \times \omega (\bar{K}^{t-1, 1}_{E}, \bar{K}^{t, 1}_{C}) + \alpha \times \omega (\bar{K}^{t, 1}_{A}, \bar{K}^{t, 1}_{E})
となる??
実験と結果
モデル、トポロジーによる精度
以下のTable 3 はモデルを1、2、3、及びトポロジーを A、B 変えてメトリクスを計測したもの。

モデルに関しては、当然1、2、3の順の精度となるが、それ以上に速度(fps)は3、2、1の順でよい。
またトポロジー A と B ではBの方が若干精度がよい。