はじめに
CVPR2018から以下の論文
[1] F. Muller, et. al. "GANerated Hands for Real-Time 3D Hand Tracking from Monocular RGB"
のまとめ
概要
- RGBの動画のみから手の3次元トラッキングをリアルタイムで行うモデル
- 学習データを水増しするため合成画像をGANでリアルに変換する
- 2D上での比較や3D上での比較を組み合わせて行う
下図 [1]Figure1 のように画像(映像)を入力すると手の3次元骨格を推定する。

アーキテクチャの全体像
下図の[1]Figure2 が全体像。

左側がデータを水増しする部分。オフラインで行う。
右側が与えられたデータに対して手の3次元トラッキングを推定する部分。ここはオンラインでリアルタイムに推定する。
GANを使ったデータの水増し部分(GeoConGAN)
GANを使ったデータの水増し部分(以下GeoConGAN)は下図の[1]Figure 3。
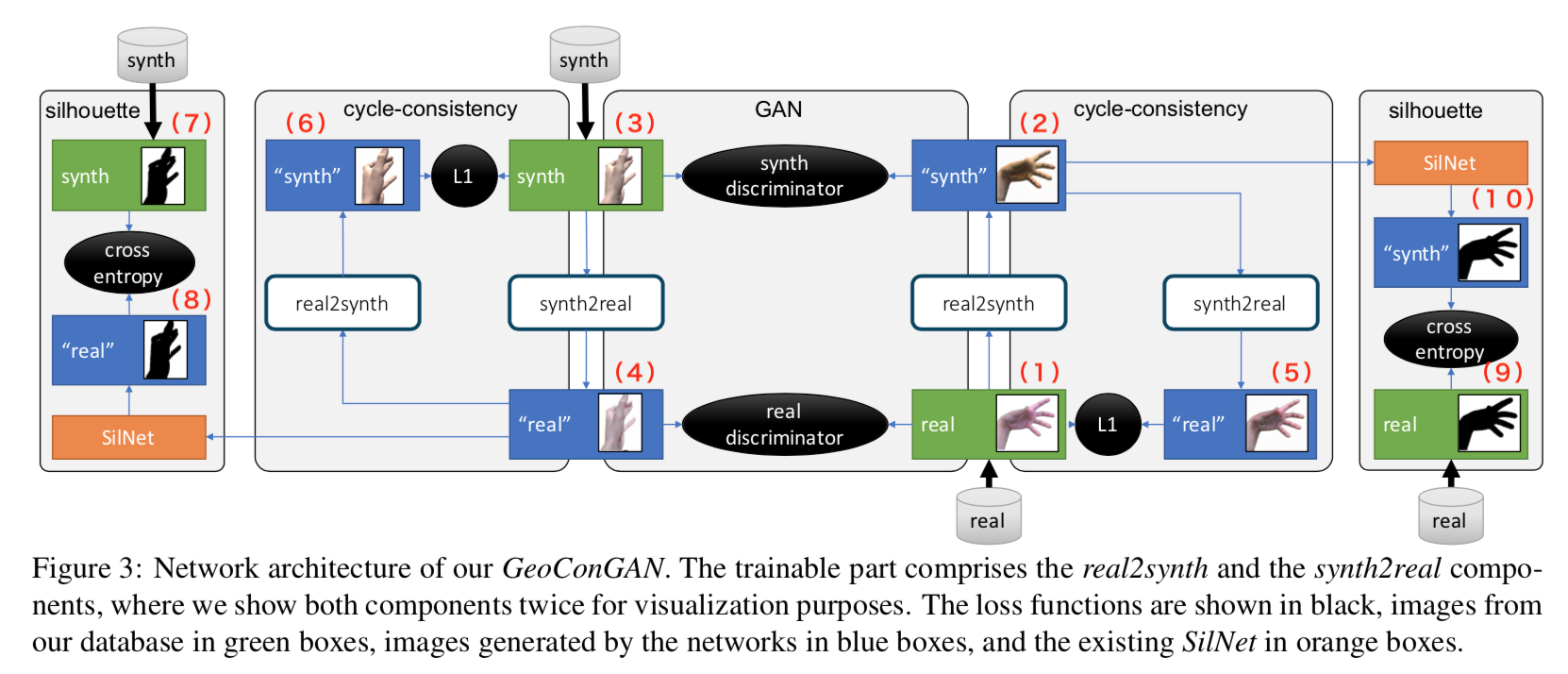
全体的には Cycle-GANの構造に近い。
ネットワークは
- realな手を合成画像に変換する real2synth
- 合成画像の手をrealに変換する synth2real
- realな手か否かを判定する real discriminator
- 合成画像の手か否かを判定する synth discriminator
の4つ。
まず中央下の右寄りからreal なイメージ(1)を入力する。その上 real2synth で合成画像(2)へ変換する。
一方中央上の左寄りから合成画像(3)の手を入力し、その下 synth2real で real な画像(4)へ変換する。
(1)と(4)を real discriminator へ入力し、discriminatorはrealな元画像か、生成されたreal画像かを見分けるよう学習する。
(2)と(3)を synth discriminator へ入力し、discriminatorは合成な元画像か、生成された合成画像かを見分けるよう学習する。
(2)の生成された合成画像はさらに synth2realへ入力して元画像(5)へ再変換する。(1)と(5)とで cycle-consistencyをとり、学習する。
一方、(4)の生成された realな画像は real2synth で合成画像(6)へ再変換される。(3)と(6)で cycle-consistency をとり学習する。
・・・と、ここまではcycle-GANそのもの。これで問題となるのは、synth2real、あるいはreal2synth で手のポーズが変わってしまうこと。
例えば、ジャンケンのグーの形をしたrealな画像をreal2synthに入力し、パーの合成画像が生成されたとする。これをsynth2realに入力して再度グーな形状のrealっぽい画像が生成されたとすると、cycle-consistencyはほぼゼロなので、1つの収束点になり得る。
しかし、合成画像の手の形状が変わってしまえば、アノテーションとの整合性がとれなくなり、trackingの学習データとしては使えない。
よって、手の形状を変えないような新たな部分を加える。具体的にはシルエット同士でcross-entropyをとる。
まず最左部で、合成画像(3)のシルエット(7)と、合成画像をreal に変換した画像(4)を学習済みSilNetへ入力して得たシルエット(8)とで交差エントロピーをとる。
同様に最右部で、real な画像(1)のシルエット(9)と、realな画像を合成画像へ変換した画像(2)を学習済みSilNetへ入力して得たシルエット(10)とで交差エントロピーをとる。
結果、合成画像は下図[1]Figure 4 のようにリアルになる。

手の tracking 部分(RegNet)
前節で作成したリアルな手画像を用いて、手のtrackingを行う部分が下図[1]Figure 6のRegNet。

RegNet の全体像
Figure 6 の左下から手の画像をResNet風なネットワークに入力し、intermediate 3D positionsを出力する。
これをProjLayerで2Dに射影したものがその右 rendered 2D heatmaps。
これにResNetからの出力を合わせたものを更に畳み込んで、2D heatmaps と 3D positionsを出力する。
運動学的な手のモデル
まず $\bf{t}\rm \in \mathbb{R}^3$ と $\bf{R}\rm \in SO(3)$ をルート関節(手首)を基準としたワールド座標、及びオイラー角とする。
$\bf \theta \rm \in \mathbb{R}^{20}$ を各手・指の関節における角度とする。関節は15個だが、それぞれ1または2の自由度を持ち、トータルで20次元となる。
この3つのパラメータを合わせて $\Theta = (\bf t,R, \theta )$ とする。
$\mathcal{M} (\Theta) \in \mathbb{R}^{J \times 3}$ を全関節( $J = 21$ )の絶対座標とする。特に $\mathcal{M}_j (\Theta) \in \mathbb{R}^{3}$ は関節 $j$ の絶対座標となる。
Lossの全体像
E(\Theta)=E_{2D}(\Theta) + E_{3D}(\Theta) + E_{limits}(\Theta) + E_{temp}(\Theta)
右辺第1項目から2次元フィッティング項、3次元フィッティング項、関節角度項、時間的平滑項。
詳細は以下。
2次元フィッティング項
2次元フィッティング項ではRegNetから出力さる2次元の関節ヒートマップ $u_j$ とターゲット(3次元ワールド座標)を2次元に投影した $\Pi (\mathcal{M}_j(\Theta))$ とでロスを計算する。
E_{2D} (\Theta) = \sum_j w_j \| \Pi (\mathcal{M}_j(\Theta)) - u_j \|_2^2
$w_j$ はヒートマップから来る関節 j の確信度。
3次元フィッティング項
3次元フィッティング項は以下。
E_{3D} (\Theta) = \sum_j \| (\mathcal{M}_j(\Theta) - \mathcal{M}_{root}(\Theta))- z_j \|_2^2
ここで $z_j \in \mathbb{R}^3$ は以下で計算する。
z_j = z_{p(j)} + \frac{\| \mathcal{M}_j(\Theta) - \mathcal{M}_{p(j)}(\Theta) \|_2}{\| x_j - x_{p(j)} \|_2} (x_j - x_{p(j)})
あえて
E_{3D} (\Theta) = \sum_j \| (\mathcal{M}_j(\Theta) - \mathcal{M}_{root}(\Theta))- (x_j - x_{root}) \|_2^2
とせずに面倒臭い計算をしているのは、人によって異なる各指部位の長さを問題としないため。
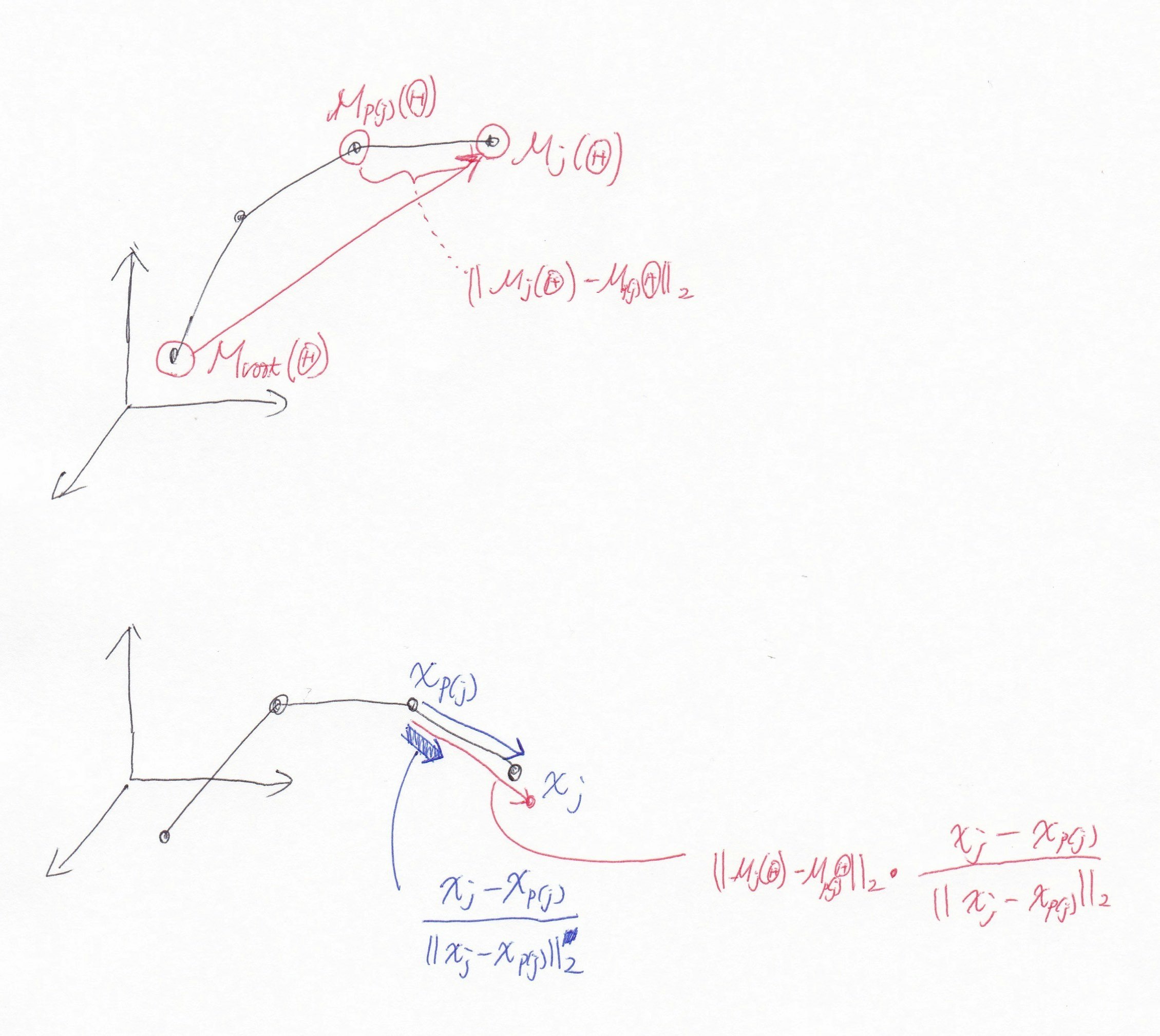
下図で考えると
まず $\mathcal{M}_j(\Theta)-\mathcal{M} _{root}(\Theta)$ は図上側のようにターゲットの基準の位置からの対象関節の位置。
$| \mathcal{M}_j(\Theta) - \mathcal{M} _{p(j)} (\Theta) | _2$ はターゲットにおける根元側の関節を基準にした対象関節の長さ。
\frac{(x_j - x_{p(j)})}{\| x_j - x_{p(j)} \|_2}
は推論値における根元側の関節を基準にした対象関節のパラメータを正規化した単位ベクトル的なもの。(図の下側)
よって
\frac{\| \mathcal{M}_j(\Theta) - \mathcal{M}_{p(j)}(\Theta) \|_2}{\| x_j - x_{p(j)} \|_2} (x_j - x_{p(j)})
は向きは推論値だが、長さはターゲットと同じになる。
関節角度項
関節角度項は $E_{limits}(\theta)$ は「指が反対側に折れ曲がってる」ようなあり得ない角度にしないための制約項。
E_{limits}(\theta) = \| \max([0, \theta-\theta^{max}, \theta ^{min} - \theta]) \|^2_2
つまり関節の可動域を上回っても下回ってもロスとなるようにしている。
時間的平滑項
時間的平滑項では前のフレームのパラメータの変化率から現在のフレームの変化率が変化しないよう、制約をかける。
E_{temp}(\Theta) = \| \triangledown \Theta ^{prev} - \triangledown \Theta \|^2_2
実験と評価
ablation study や他のモデルとの比較は下図[1] Figure 7。
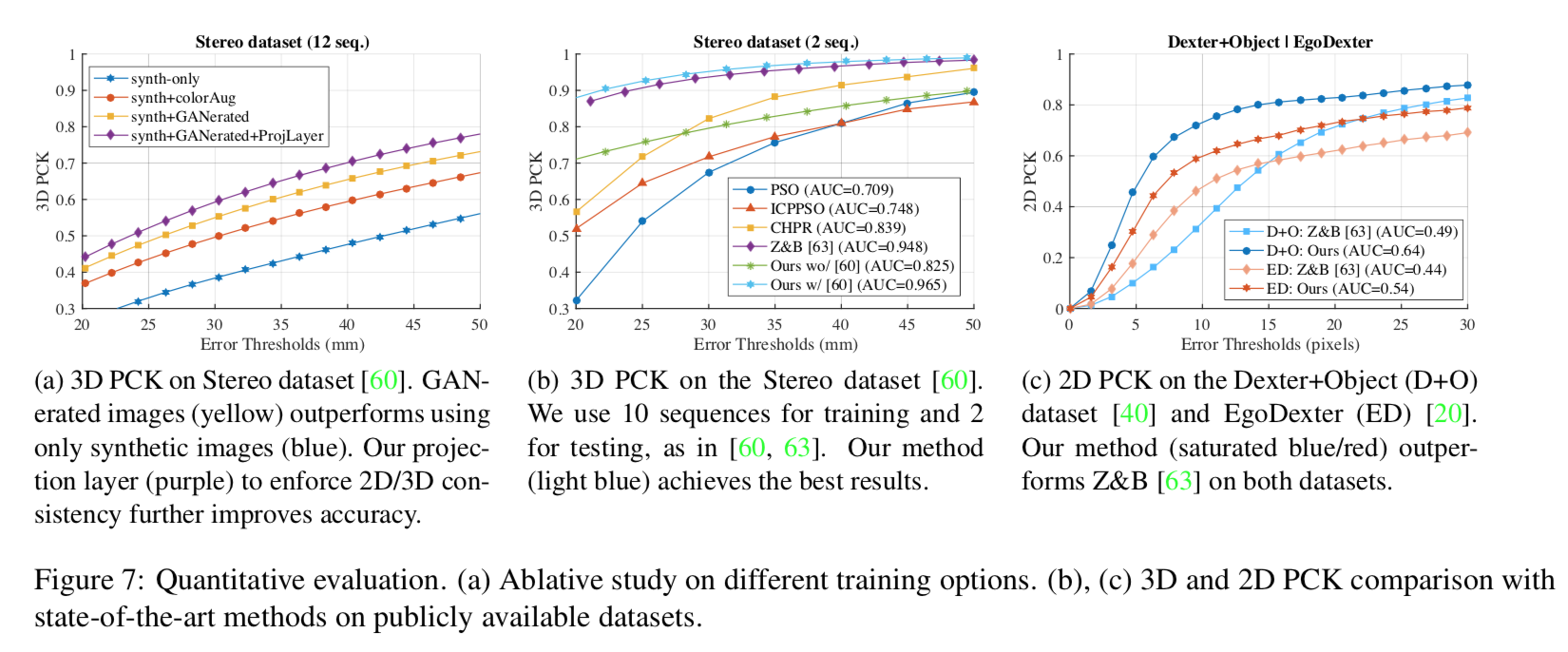
メトリクスはいずれもPCK(Percentage of correct keypoints score)。
GANの部分のablative study
Figure 7 の左側図。3DのStereo datasetsで比較。
青色の線が合成画像。それに対して色を変えるaugmentationをしたものが赤色の線。それに対してProjLayerなしのGaneratedしたものが黄色の線、ProjLayerありのGeneratedしたものが紫色の線。
本GANモデルをフルに使用したものが一番性能がいい。
他のモデルとの比較
3DのStereo datasetsで比較したグラフが Figure 7 の中央。
水色の本手法が他の手法を上回っている。
2DのDexter+Object datasetで比較したものが Figure 7 の右。
本手法が Z&B を上回っている。