ホップフィールドネットワーク・ボルツマンマシン・制限付きボルツマンマシンについて

はじめに

ホップフィールドネットワーク，ボルツマンマシンと制限付きボルツマンマシンについてここでは解説する．　過去の研究が現在の研究に新たな見地を与えるのではないかということを目的として記す．

ホップフィールドネットワーク

http://e-musu.github.io/ml/2016/02/10/hopfield-network
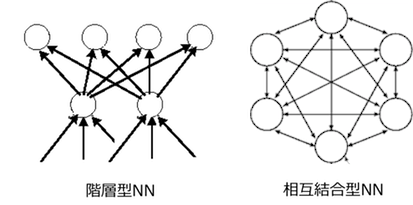
上のように，ニュールラルネットワーク（NN）には階層型と相互結合型の大きく分けて２種類が存在する．
ホップフィールドは相互結合型NNである

ユニットiとjの結合係数をw_{ij}，ユニットiの結合係数を-\theta_i,ユニットの出力結果をx_i = 0　or　1とする.\\

エネルギーE = -(\sum_{i<j} w_{ij} x_i x_j+\sum_i \theta_i  x_i)\\
=-(\sum_{i ne j} w_{ij} x_j + theta_i)x_i + (x_iを含まない項)　ー（１）\\
なので
\sum_{i ne j} w_{ij} x_j + \theta_iが正の時はx_iは１
\sum_{i ne j} w_{ij} x_j + \theta_iが負の時はx_iは０とする操作を行うと\\
Eは減少する．よってこの操作を繰り返していくと，Eが極小値を取る点で安定し，出力結果が安定化する．

このように閾値ーθをもとに，ユニットの出力結果を更新していくことで最終的に安定した出力結果に落ち着くことが，数式からわかる．

ボルツマンマシン

ボルツマンマシンも相互結合型NNである．エネルギーEの式も等しい．ボルツマンマシンになって異なる部分は統計力学における温度という概念を持ち込んだ点である．

x_iが1の時と0の時のエネルギーの差は（１）よりΔ E =-(\sum_{i \ne j} w_{ij} x_j + \theta_i)-(2)と出せる．\\
一方で，統計力学においてよく用いられるカノニカル集合ではエネルギーEを取る確率がexp(-E/kT)と表せて,\\
x_i=1となる確率をp，x_i=0となる確率を1-pとおくと，\\
x_iが1の時と0の時のエネルギーの差はΔ E =(-kTlog(p))- (-kTlog(1-p))=kTlog(1/p-1)\\
p=1/(1+ exp(Δ E / kT))\\

ホップフィールドの場合，Δ E が正であれば必ず出力を1，負であれば必ず出力を０にするというものであったが，ボルツマンマシンの場合, Δ E が正であれば50％以上で出力を1，負であれば50%以上で出力を０にする．　その確率は温度　Tに依存しており，Tが０に近いと，確実にEが減少するホップフィールドネットワークに近づく．Tが無限大に近いと出力=1 or 0の確率が，ΔEに関係なく両方とも1/2に近づき乱雑さを増す．
最初はTを高温にして，徐々にTの温度を低くすることがよく行われる．これの意図は最初はTの温度を上げた状態で，乱雑に動かすことで，　小さな極小値から抜け出し，　大きな極小値を見つけたあたりでTの温度を下げて，安定させるといったところである．

制限付きボルツマンマシン

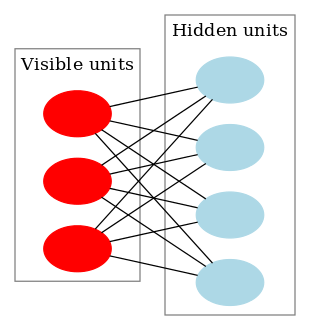
　制限付きボルツマンマシンは上の一般的なボルツマンマシンを階層型NNに変えたものである．

https://ja.wikipedia.org/wiki/%E3%83%9C%E3%83%AB%E3%83%84%E3%83%9E%E3%83%B3%E3%83%9E%E3%82%B7%E3%83%B3
ボルツマンマシンにおいて，visible unitsとhidden unitsの二種類のレイヤーに分け，同じレイヤーに属するユニットは結び付けないようにしたものを，制限付きボルツマンマシンと呼ぶ．　unit間を全結合しなくてよいので計算量が減り，ボルツマンマシンの問題点である収束速度を早めることにつながる．

次回

今回述べたものが現在どのように応用されているかについて述べたい．

Reference

ホップフィールドネットワークhttps://ja.wikipedia.org/wiki/%E3%83%9B%E3%83%83%E3%83%97%E3%83%95%E3%82%A3%E3%83%BC%E3%83%AB%E3%83%89%E3%83%BB%E3%83%8D%E3%83%83%E3%83%88%E3%83%AF%E3%83%BC%E3%82%AF
ボルツマンマシン
https://ja.wikipedia.org/wiki/%E3%83%9C%E3%83%AB%E3%83%84%E3%83%9E%E3%83%B3%E3%83%9E%E3%82%B7%E3%83%B3
カノニカル集合
https://kotobank.jp/word/%E3%82%AB%E3%83%8E%E3%83%8B%E3%82%AB%E3%83%AB%E9%9B%86%E5%90%88-46037
Qiitaの数式チートシート
http://qiita.com/iizukak/items/04d6e226982bc108bc16