はじめまして、大学で量子アニーリングの研究をしています。記事を投稿するのは初めてなのですが、量子コンピュータAdvent Calendar 2018その2が後半少し寂しげだったので、量子アニーリングに関する記事、もといQuTiP布教記事を書いてみることにしました。
QuTiPとは
QuTiPは、量子系の数値計算に特化したPythonライブラリで、「Quantum Toolbox in Python」の略です。本記事では、QuTiPの簡単な使い方と量子アニーリング研究における活用事例をいくつか紹介します。
使用したPythonのバージョンはPython 3.6.1です。2系の人は適宜読み替えてください。
(追記:Python 2だと使えないという情報をいただきました。3じゃないと使えないかもしれません。)
また、詳しい使い方などの情報は公式サイト
http://qutip.org/
を参照してください。
はじめに、インストールは
$ pip install qutip
とする、もしくは、Anacondaの場合はconda-forgeチャンネルを有効にして
$ conda install qutip
とすればできます。チャンネルってなんぞやという人は
$ anaconda search -t conda qutip
で出てきた中から、それっぽいのを指示に従ってインストールすればできます。URLが変わっていなければ、おそらく次のコマンドでインストールできます。
$ conda install --channel https://conda.anaconda.org/conda-forge qutip
簡単な使い方
まずは、QuTiPライブラリをインポートします。
from qutip import *
量子力学における状態や演算子は、QuTiPにおいてはQobjというクラスのオブジェクトとして表されます。例えば、
\lvert 0\rangle=\begin{pmatrix}
1 \\
0
\end{pmatrix}
という量子状態を作りたかったら、
ket0 = Qobj([[1], [0]])
とします。変数ket0の中身を見てやると、
>>> ket0
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]]
となっており、ケットベクトルであることまでちゃんと認識されています。QuTiPでは、このような標準基底 $\lvert 0\rangle, \lvert 1\rangle$(あるいは、$\lvert\uparrow\rangle, \lvert\downarrow\rangle$)などのよく使う状態や演算子は、簡単に使えるようにすでに用意されていて、例えば $\lvert 0\rangle, \lvert 1\rangle$ は
basis(2, 0), basis(2, 1)
で得ることができます。第1引数が考える空間の次元、第2引数がその空間で何番目の基底かを表します。また、量子計算でよく使うパウリ行列 $\sigma^x, \sigma^y, \sigma^z$ は
sigmax(), sigmay(), sigmaz()
と表されます。ついでに、単位行列は
qeye(2)
です。引数は考える空間の次元です。
このままでは1スピンの空間しか扱えず、多スピンの系が扱えませんが、QuTiPには多スピン系も扱えるようにテンソル積を行う関数が用意されています。例えば、2スピンの系で $\lvert 01\rangle$ という状態を作りたかったら
>>> tensor(basis(2, 0), basis(2, 1))
Quantum object: dims = [[2, 2], [1, 1]], shape = (4, 1), type = ket
Qobj data =
[[ 0.]
[ 1.]
[ 0.]
[ 0.]]
とします。また、$\sigma_1^z \sigma_2^z$($=\sigma_1^z\otimes\sigma_2^z$)という演算子を考えたかったら、
>>> tensor(sigmaz(), sigmaz())
Quantum object: dims = [[2, 2], [2, 2]], shape = (4, 4), type = oper, isherm = True
Qobj data =
[[ 1. 0. 0. 0.]
[ 0. -1. 0. 0.]
[ 0. 0. -1. 0.]
[ 0. 0. 0. 1.]]
とします。一気に複数のテンソル積を行いたかったら、引数としてリストを渡すことでできます。
>>> tensor([sigmaz() for i in range(3)])
Quantum object: dims = [[2, 2, 2], [2, 2, 2]], shape = (8, 8), type = oper, isherm = True
Qobj data =
[[ 1. 0. 0. 0. 0. 0. 0. 0.]
[ 0. -1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. -1. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 0. 0. 0. 0.]
[ 0. 0. 0. 0. -1. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 0. 0. 0. -1.]]
ハミルトニアンの固有状態や固有エネルギーは
evals = H.eigenenergies()
evals, ekets = H.eigenstates()
eval0, eket0 = H.groundstate()
などで求めることができます。上からそれぞれ、全部の固有エネルギー、全部の固有エネルギーと固有状態、基底エネルギーと基底状態、を求めます。例えば $H=\sigma^x$ の固有エネルギーと固有状態を全部求めたかったら、
>>> H = sigmax()
>>> evals, ekets = H.eigenstates()
>>> evals
array([-1., 1.])
>>> ekets
array([ Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[-0.70710678]
[ 0.70710678]],
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.70710678]
[ 0.70710678]]], dtype=object)
となります。
その他にも、エルミート共役やトレース、部分トレースなど、量子力学でよく出てくる演算は一通りできるようになっているので、詳しくは公式ドキュメントを参照してください。
エネルギースペクトルの計算
ここからは、量子アニーリングにおける応用を紹介していきます。今回考えるハミルトニアンは
H(s)=sH_0+(1-s)H_1
という形のハミルトニアンです。ただし、$H_0$ は解きたい問題のハミルトニアン、$H_1$ は横磁場のハミルトニアンです。
H_0=-\sum_{i<j}J_{ij}\sigma_i^z\sigma_j^z-\sum_{i=1}^{N}h_{i}\sigma_i^z,\quad H_1=-\sum_{i=1}^{N}\sigma_i^x
まずは、QuTiPライブラリと今回使う他のライブラリをインポートします。
import numpy as np
from qutip import *
import matplotlib.pyplot as plt
import random
今回は、簡単に4スピン系とします。相互作用係数 $J_{ij}$ と縦磁場 $h_i$ は今回、辞書型で作ってやります。せっかくなので、ランダムな相互作用と縦磁場を考えましょう。
N = 4
J = {}
h = {}
for i in range(N-1):
for j in range(i+1, N):
J[(i, j)] = random.gauss(0, 1)
for i in range(N):
h[i] = random.gauss(0, 1)
今回作られた相互作用と縦磁場は
>>> J
{(0, 1): 0.8661383462807593, (0, 2): 0.8287409863979471, (0, 3): -0.25709516560752205, (1, 2): 0.3640646975581623, (1, 3): 0.17000051132424981, (2, 3): 1.2274289990533989}
>>> h
{0: 0.20524076873394545, 1: 0.8192607934001573, 2: -0.6322639149536304, 3: -0.7572121854611877}
となりました。
次にスピン演算子 $\sigma_i^z, \sigma_i^x$ を作ります。これはテンソル積を使えば作れます。1行で書いているので少し分かりづらいかもしれませんが、ここでは、スピン演算子 $\sigma_i^z$ を要素に持つリストszを作っています。各スピン演算子 $\sigma_i^z$ は、$i$番目が $\sigma^z$ でそれ以外が単位行列のテンソル積なのでこのようになります。sxも同様です。
sz = [tensor([sigmaz() if i == j else qeye(2) for j in range(N)]) for i in range(N)]
sx = [tensor([sigmax() if i == j else qeye(2) for j in range(N)]) for i in range(N)]
次に、ハミルトニアン $H_0$ を作ります。
H0 = 0
for i in range(N-1):
for j in range(i+1, N):
H0 += -J[(i, j)]*sz[i]*sz[j]
for i in range(N):
H0 += -h[i]*sz[i]
$H_1$ は簡単に、
H1 = -sum(sx)
と書けます。
いよいよエネルギースペクトルの計算です。パラメータ $s$ を 0 から 1 まで動かしたときに、ハミルトニアン $H(s)$ の固有エネルギーがどう変化するかを調べます。
slist = np.linspace(0.0, 1.0, 101)
Elists = [[] for i in range(2**N)]
for s in slist:
H = s*H0 + (1-s)*H1
evals = H.eigenenergies()
for i in range(2**N):
Elists[i].append(evals[i])
計算ができたので、プロットしてみましょう。
for i in range(2**N):
plt.plot(slist, Elists[i])
plt.show()
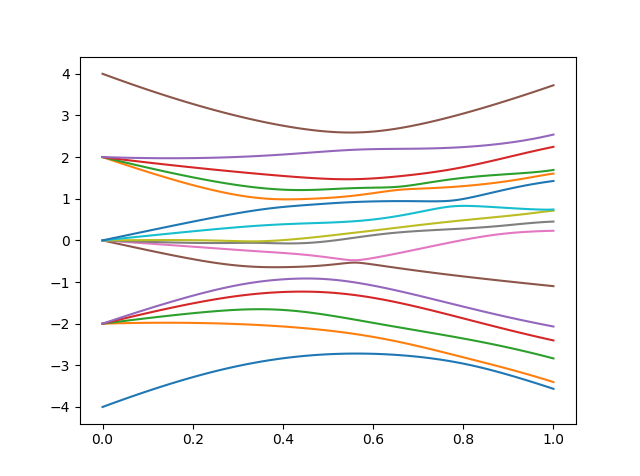
結果は下図の様になりました。いくつかの点で擬交差(エネルギースペクトル線がスレスレまで近づくこと)が起きているのが確認できます。基底状態について見てみると $s=0.8$ 付近で第1励起状態に近づいていて、そこら辺で注意しないと最終的に基底状態が得られない可能性があることなどが分かりそうです。
アニーリングの成功確率の計算
次に、量子アニーリングのダイナミクスを計算して、アニーリングの成功確率を求めてみます。先程のハミルトニアン $H(s)$ において $s=t/T$ とおいてアニーリング時間 $T$ を定義します。量子アニーリングでは $T$ を十分長く取れば、原理的には 100% の確率で基底状態が得られます。そこで、$T$ を適当に変えてみて量子アニーリングを行い、最終的に得られる状態 $\lvert\psi(T)\rangle$ が $H_0$ の基底状態 $\lvert\phi_0\rangle$ をどれくらい含んでいるか $\lvert\langle\phi_0|\psi(T)\rangle\rvert^2$ を見てやります。これを量子アニーリングの成功確率と呼ぶことにします。
量子アニーリングはシュレーディンガー方程式に従って時間発展しますが、QuTiPでは簡単なコードでそのシュレーディンガー方程式を数値的に解くことができます。
まずは、$\lvert\phi_0\rangle$ を求めておきます。
_, eket0 = H0.groundstate()
つぎに、$H_0$ と $H_1$ の係数を関数の形で用意してやります。
T = 10.0
def f0(t, args):
return t/T
def f1(t, args):
return 1 - t/T
全体のハミルトニアンは、各ハミルトニアンとその係数の2つ組のリストを要素に持つリストで与えてやります。
H = [[H0, f0], [H1, f1]]
$t=0$ における初期状態を作ります。これは $H_1$ の基底状態です。
psi0 = tensor([Qobj([[1], [1]])/np.sqrt(2) for i in range(N)])
今回は成功確率だけじゃなく、各時刻で $\lvert\psi(t)\rangle$ が $\lvert\phi_0\rangle$ をどれくらい含んでいるかまで見てみることにします。シュレーディンガー方程式を解くにはmesolveを使います。詳しい説明は省略しますが、解きたいハミルトニアン(時間に依存していても良い)と、初期状態、時間のリスト、謎のリスト(Collapse operatorなるもものリスト。今回は特に関係ない)、各時刻で期待値を計算したい演算子のリスト(今回は $\rho=\lvert\phi_0\rangle\langle\phi_0\rvert$ の期待値。ket2dmはケットベクトルを密度演算子に変換する関数)を与えると、ダイナミクスを計算してくれます。
tlist = np.linspace(0.0, T, 101)
result = mesolve(H, psi0, tlist, [], [ket2dm(eket0)])
計算結果のうち、計算してほしかった期待値 $\lvert\langle\phi_0|\psi(t)\rangle\rvert^2$ の部分はresult.expect[0]に格納されています。プロットしてみましょう。
plt.plot(result.times, result.expect[0])
plt.show()
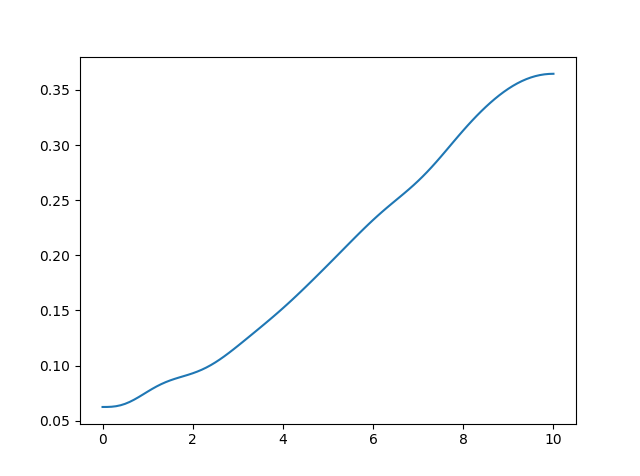
アニーリングが進むたび、$\lvert\psi(t)\rangle$ が $\lvert\phi_0\rangle$ を含む割合が増えていることが分かります。最終的な成功確率は 0.35 ちょい上くらいとあんまり良い結果とはなりませんでした。
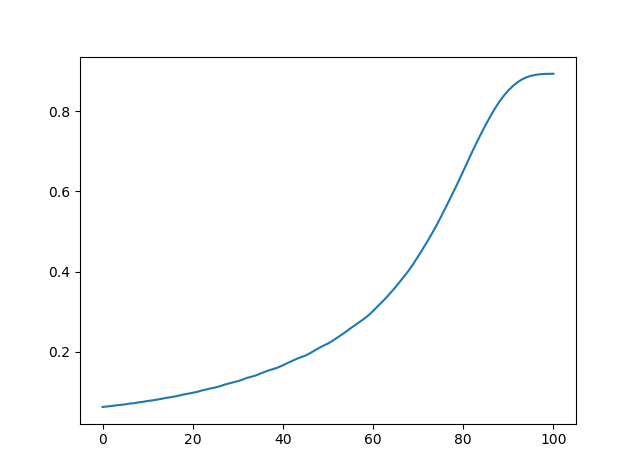
先程は $T=10$ でしたが、今度はアニーリング時間を $T=100$ まで増やしてみましょう。結果は下図のようになりました。さっきは 0.35 ちょいだった成功確率が、0.9 くらいまで上がっているのが分かります。アニーリング時間を増やせば成功確率も高くなることが確かめられました。
おわりに
今回は、QuTiPの簡単な使い方と、量子アニーリング(の基礎研究)における活用事例としてエネルギースペクトルの計算と成功確率の計算を紹介してみました。基礎よりの話になってしまい果たして読者がいるのか謎ですが、ここまで読んでいただきありがとうございました。QuTiPの使い方に関しては紹介しきれなかった部分もあり、また私自身も熟知しているわけではないので至らない点もあるかと思います。何かありましたら指摘なり質問なりしていただけると幸いです。
最後に、今回のソースコードの全文を載せておきます。
ソースコード全文
import numpy as np
from qutip import *
import matplotlib.pyplot as plt
import random
N = 4
J = {}
h = {}
for i in range(N-1):
for j in range(i+1, N):
J[(i, j)] = random.gauss(0, 1)
for i in range(N):
h[i] = random.gauss(0, 1)
sz = [tensor([sigmaz() if i == j else qeye(2) for j in range(N)]) for i in range(N)]
sx = [tensor([sigmax() if i == j else qeye(2) for j in range(N)]) for i in range(N)]
H0 = 0
for i in range(N-1):
for j in range(i+1, N):
H0 += -J[(i, j)]*sz[i]*sz[j]
for i in range(N):
H0 += -h[i]*sz[i]
H1 = -sum(sx)
# ここからエネルギースペクトルの計算
slist = np.linspace(0.0, 1.0, 101)
Elists = [[] for i in range(2**N)]
for s in slist:
H = s*H0 + (1-s)*H1
evals = H.eigenenergies()
for i in range(2**N):
Elists[i].append(evals[i])
for i in range(2**N):
plt.plot(slist, Elists[i])
plt.show()
# ここから成功確率の計算
_, eket0 = H0.groundstate()
T = 10.0
def f0(t, args):
return t/T
def f1(t, args):
return 1 - t/T
H = [[H0, f0], [H1, f1]]
psi0 = tensor([Qobj([[1], [1]])/np.sqrt(2) for i in range(N)])
tlist = np.linspace(0.0, T, 101)
result = mesolve(H, psi0, tlist, [], [ket2dm(eket0)])
plt.plot(result.times, result.expect[0])
plt.show()