前回の記事では、テッセレーションシェーダーでポリゴン分割を行なってからひび部分を凹ませるシェーダーを作りました。
今回は、テッセレーションにPN-Trianglesを適用してみます。
シリーズ目次
PN-Trianglesについて
正式には Curved Point-Normal Tringnales と言います。
物凄く簡単に書くと、ポリゴン分割して新しい頂点を設定するときに、そのポリゴンの平面上ではなく、各頂点の接平面から算出した曲面上に新しい頂点を配置するというアルゴリズムです。
ホワイトペーパーはこちら。
解説記事もチラホラあるのですが、本家が一番理解しやすかったです。
実装はPN-AENのホワイトペーパーをベースにしました。
PN-AENとは Crack-Free Point-Normal Triangles using Adjacent Edge Normal の略称で、PN-Trianglesの「隣接するポリゴンとの間にクラックが発生することがある」という欠点を改良したバージョンです。
本当はPN-AENで実装したかったのですが、前提としている D3D11_PRIMITIVE_TOPOLOGY_X_CONTROL_POINT_PATCHLIST の設定をUnityで行う方法がわからず、PN-Trianglesでの実装となりました。
PN-Trianglesでテッセレーション
Hull-Shader Stage
メインハルシェーダーは変化ありません。
パッチ定数関数の方に処理を追加します。
パッチ定数関数ではポリゴンの3頂点の情報を参照することができるので、ここで後に必要となる座標を算出し、返却値の構造体に忍ばせておきます。
パッチ定数関数内のPN-Triangles用処理のコード
static float OneThird = rcp(3.0);
static float OneSixth = rcp(6.0);
struct patchConstParam {
float edgeTessFactors[3] : SV_TessFactor;
float insideTessFactor : SV_InsideTessFactor;
// PN-Triangles計算用のコントロールポイント
float3 b111 : TEXCOORD0;
float3 positionsOS[3][3] : TEXCOORD1;
};
/**
* [パッチ定数関数用]
* PN-Triangles用のコントロールポイントを算出する
*/
float3 CalcControlPointForPnTri(float3 posA, float3 posB, float3 normalA) {
// PosAとPosBを結ぶ線分を1:2に分けた地点をPosAの接平面上に移動した座標を算出
return (2.0 * posA + posB - (dot((posB - posA), normalA) * normalA)) * OneThird;
}
/**
* [パッチ定数関数用]
* PN-TrianglesのB111の位置を計算する
*/
float3 CalcPnTriB111Pos(float3 controlPoints[3][3]) {
float3 b300 = controlPoints[0][0];
float3 b210 = controlPoints[0][1];
float3 b120 = controlPoints[0][2];
float3 b030 = controlPoints[1][0];
float3 b021 = controlPoints[1][1];
float3 b012 = controlPoints[1][2];
float3 b003 = controlPoints[2][0];
float3 b102 = controlPoints[2][1];
float3 b201 = controlPoints[2][2];
float3 e = (b210 + b120 + b021 + b012 + b102 + b201) * OneSixth;
float3 v = (b003 + b030 + b300) * OneThird;
return e + ((e - v) * 0.5);
}
/**
* パッチ定数関数
*/
patchConstParam PatchConstantFunc(InputPatch<v2d, 3> inputs) {
patchConstParam output;
[unroll]
for (i = 0; i < 3; i++) {
uint nextId = (i + 1) % 3;
output.positionsOS[i][0] = inputs[i].positionOS.xyz;
output.positionsOS[i][1]
= CalcControlPointForPnTri(inputs[i].positionOS.xyz, inputs[nextId].positionOS.xyz, inputs[i].normalOS);
output.positionsOS[i][2]
= CalcControlPointForPnTri(inputs[nextId].positionOS.xyz, inputs[i].positionOS.xyz, inputs[nextId].normalOS);
}
output.b111 = CalcPnTriB111Pos(output.positionsOS);
return output;
}
Domain-Shader Stage
ドメインシェーダーでは、引数で渡ってきた頂点候補をそのまま使うのではなく、曲面に位置するように変位させます。
パッチ定数関数の返却値で渡した値が引数に入ってくるので、事前に求めていた値を利用することができます。
法線については、こちらも曲面上に取ってしまうと、その後ひび模様部分を法線と逆方向に凹ませるときに凹んだ頂点が他のひび模様の上に突き出してしまうリスクが高まるので、PN-Trianglesを適用しない場合と同じフラットなポリゴン上に取るようにしました。
PN-AENでも法線を曲面上に取るとクラックが発生しやすくなると言う理由でフラットポリゴン上に取る実装になっていました。
ドメインシェーダー内のPN-Triangles用処理のコード
// CulcSubdevidedPos()はその3に同じ
/**
* ドメインシェーダー
*/
[domain("tri")]
d2f Domain(patchConstParam param, const OutputPatch<v2d, 3> inputs, float3 baryCentricCoords:SV_DomainLocation) {
d2f output;
// まずはフラットなポリゴン上に算出された座標を求める
// 算出された座標を重心座標系からローカル座標等に換算
float3 srcLocalPositions[3];
float3 srcLocalNormals[3];
float3 srcUVs[3];
float3 srcWorldTangents[3];
[unroll]
for (uint i = 0; i < 3; i++) {
srcLocalPositions[i] = inputs[i].positionOS.xyz;
srcLocalNormals[i] = inputs[i].normalOS;
srcUVs[i] = float3(inputs[i].uv, 0.0);
}
float3 flatLocalPos = CalcSubdividedPos(srcLocalPositions, baryCentricCoords);
output.uv = CalcSubdividedPos(srcUVs, baryCentricCoords).xy;
// 法線についてはPN-Trianglesで計算するとひび用の頂点移動時に亀裂が発生しやすくなるので、フラットなポリゴンの法線を採用
float3 localNormal = CalcSubdividedPos(srcLocalNormals, baryCentricCoords);
output.initNormalOS = localNormal;
output.initNormalWS = TransformObjectToWorldNormal(localNormal);
// PN-Trianglesを用いてカーブ上になるように座標変位
float3 pnTriLocalPos = CalcPnTriPosition(param.positionsOS, param.b111, baryCentricCoords);
output.initPositionOS = lerp(flatLocalPos, pnTriLocalPos, _PnTriFactor);
// 頂点がひび模様に重なる場合は凹ませる
output.positionOS = CalcCrackedPos(output.initPositionOS, output.initNormalOS, output.initNormalWS, output.crackLevel);
output.positionCS = TransformObjectToHClip(output.positionOS);
return output;
}
元のポリゴンの三角形の辺上に増やす頂点にはPN-Trianglesを適用しないオプション追加
モデルによっては、ポリゴンの三角形の辺上に増やす頂点を変位させてしまうと隣接する三角形との間にクラックが生じてしまうことがありました。
これを防ぐため、辺上の頂点にはPN-Trianglesを適用せずフラットポリゴン上に頂点を生成できるオプションを用意しました。
ドメインシェーダーの引数の座標は重心座標系となっているので、XYZどれかが0付近の場合は三角形の辺上の座標であると判断できます。
/**
* ドメインシェーダー
*/
[domain("tri")]
d2f Domain(patchConstParam param, const OutputPatch<v2d, 3> inputs, float3 baryCentricCoords:SV_DomainLocation) {
// 省略
// PN-Trianglesを適用すると亀裂が発生する場合はポリゴンの辺上の頂点は変位させない
// (重心座標系では頂点から向かいの辺に向かって座標が1→0と変化することを利用)
bool isOnSides = min(min(baryCentricCoords.x, baryCentricCoords.y), baryCentricCoords.z) == 0;
if (!_AdaptsPolygonEdgeToPnTri && isOnSides) {
output.initPositionOS = flatLocalPos;
} else {
// PN-Trianglesを用いてカーブ上になるように座標変位
float3 pnTriLocalPos = CalcPnTriPosition(param.positionsOS, param.b111, baryCentricCoords);
output.initPositionOS = lerp(flatLocalPos, pnTriLocalPos, _PnTriFactor);
}
// 省略
}
適用結果
Cubeで確認(3分割)
PN-Trianglesはポリゴンの面と法線の角度を見てカーブを形成するので、Cubeのような法線がポリゴンの面の垂線となっているモデルでは未適用時と同じ結果になります。
このため、わかりやすく変化が見られるように、Cubeのメッシュをコピーして編集しました。
各法線を、それぞれ頂点が重なっている法線内の平均の方向に変更しました。
メッシュの編集はこちらのコンポーネントで行いました。
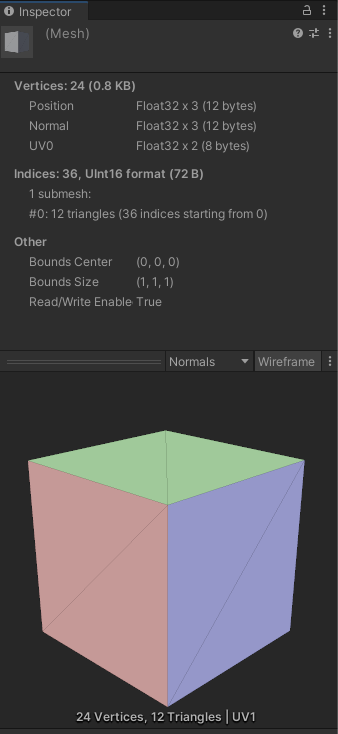
インスペクタで見ると、法線の方向が各面ごとに一定ではなくなっているのがわかります。
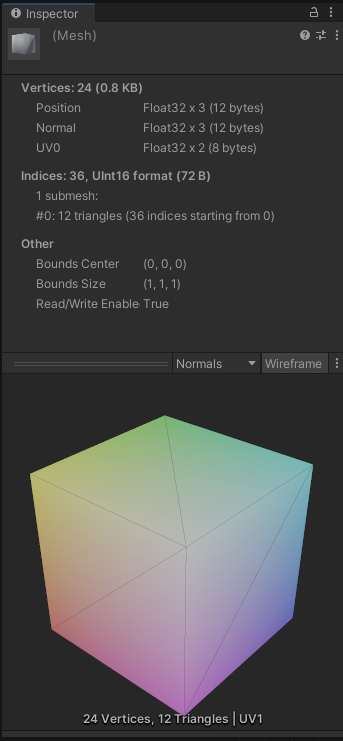
この状態でPN-Trianglesを適用したテッセレーションを行うと、全体的に膨らんで丸っこくなりました。
ひび模様も曲面上に描くことになり、丸みを帯びています。
PN-Triangles適用無し
PN-Triangles適用後
Sphereで確認(100分割)
Sphereのようにポリゴン数が多いものは形状の変化はわかりません。
ひび模様は僅かに丸みを帯びて、縁に広がりました。
見比べると、確かに適用後の方が球体であることを感じられるようになっています。
PN-Triangles適用無し
PN-Triangles適用後
その他のモデルで確認
山のモデルに適用しました。
分割無し、ひびによる凹み無し
分割無し、ひびによる凹み有り
ポリゴンの大きさに対してひび模様が細かいため不自然な影が入るようになってしまいました。

100分割、PN-Triangles適用無し
100分割、PN-Triangles適用後
PN-Trianglesを適用すると窪んでいる部分がより窪み、影が入るようになりました。
ひび模様も地形に沿ったものとなり、立体感がアップしました。
また輪郭が全体的に膨らんで丸っこいフォルムとなっています。

コード全文
コード全文です。
モデルによって良さげなPN-Trianglesの適用具合が変わってくるので、シェーダープロパティでPN-Triangles適用具合を調整できるようにしました。
ライティングはLitシェーダーの関数を利用しています。
ひび入れシェーダー(PN-Triangles編)コード全文
Shader "Custom/Crack" {
Properties {
[Header(Albedo)]
[MainColor] _BaseColor("Base Color", Color) = (1.0, 1.0, 1.0, 1.0)
[MainTexture] _BaseMap("Base Map", 2D) = "white" {}
[Header(Metallic and Smoothness)]
_Smoothness("Smoothness", Range(0.0, 1.0)) = 0.0
_Metallic("Metallic", Range(0.0, 1.0)) = 0.0
[NoScaleOffset] _MetallicGlossMap("Metallic and Smoothnes Map", 2D) = "white" {}
[Header(Crack)]
_CrackProgress("クラック進行具合", Range(0.0, 1.0)) = 0.0
[HDR] _CrackColor("クラック色", Color) = (0.0, 0.0, 0.0, 1.0)
_CrackDetailedness("クラック模様の細かさ", Range(0.0, 8.0)) = 3.0
_CrackDepth("クラックの深さ", Range(0.0, 1.0)) = 0.5
_CrackWidth("クラックの幅", Range(0.01, 0.1)) = 0.05
_CrackWallWidth("クラックの壁部分の幅", Range(0.001, 0.2)) = 0.08
// フラグメントシェーダーでクラック対象かどうかの再計算を行うかどうか
[Toggle] _DrawsCrackWithPixelUnit("ピクセル単位でクラック模様の再計算を行うか", Int) = 0
[Space]
_RandomSeed("クラック模様のランダムシード(非負整数のみ可)", Int) = 0
[Header(SubdividingPolygon)]
_SubdividingCount("細分化時に辺をいくつに分割するか(1以下は分割無し)", Int) = 1
_SubdividingInsideScaleFactor("細分化時のポリゴン内部への新ポリゴン生成度合い", Range(0.0, 1.0)) = 1.0
_PnTriFactor("PN-Triangles適用係数", Range(0.0, 1.0)) = 1.0
[Toggle] _AdaptsPolygonEdgeToPnTri("PN-Trianglesを辺にも適用するかどうか", Int) = 1
}
SubShader {
Tags {
"RenderType" = "Opaque"
"RenderPipeline" = "UniversalPipeline"
"UniversalMaterialType" = "Lit"
}
LOD 300
HLSLINCLUDE
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Core.hlsl"
ENDHLSL
Pass {
Name "Crack"
Tags { "LightMode" = "UniversalForward" }
HLSLPROGRAM
// -------------------------------------
// Material Keywords
#pragma shader_feature_local_fragment _ALPHATEST_ON
#pragma shader_feature_local_fragment _ALPHAPREMULTIPLY_ON
#pragma shader_feature_local_fragment _SPECULARHIGHLIGHTS_OFF
#pragma shader_feature_local_fragment _ENVIRONMENTREFLECTIONS_OFF
#pragma shader_feature_local_fragment _SPECULAR_SETUP
#pragma shader_feature_local _RECEIVE_SHADOWS_OFF
// -------------------------------------
// Universal Pipeline keywords
#pragma multi_compile _ _MAIN_LIGHT_SHADOWS
#pragma multi_compile _ _MAIN_LIGHT_SHADOWS_CASCADE
#pragma multi_compile _ _ADDITIONAL_LIGHTS_VERTEX _ADDITIONAL_LIGHTS
#pragma multi_compile_fragment _ _ADDITIONAL_LIGHT_SHADOWS
#pragma multi_compile_fragment _ _SHADOWS_SOFT
//--------------------------------------
// GPU Instancing
#pragma multi_compile_instancing
#include "Packages/com.unity.render-pipelines.universal/Shaders/LitInput.hlsl"
#include "Packages/com.unity.render-pipelines.universal/Shaders/LitForwardPass.hlsl"
#pragma vertex Vert
#pragma hull Hull
#pragma domain Domain
#pragma fragment Frag
#pragma require tessellation tessHW
// ---------------------------------------------------------------------------------------
// 変数宣言
// ---------------------------------------------------------------------------------------
float _CrackProgress;
half4 _CrackColor;
float _CrackDetailedness;
float _CrackDepth;
float _CrackWidth;
float _CrackWallWidth;
bool _DrawsCrackWithPixelUnit;
uint _RandomSeed;
int _SubdividingCount;
float _SubdividingInsideScaleFactor;
float _PnTriFactor;
bool _AdaptsPolygonEdgeToPnTri;
static float OneThird = rcp(3.0);
static float OneSixth = rcp(6.0);
// ---------------------------------------------------------------------------------------
// 構造体
// ---------------------------------------------------------------------------------------
struct v2d {
float4 positionOS : POSITION;
float2 uv : TEXCOORD0;
float3 normalOS : NORMAL;
float3 normalWS : TEXCOORD1;
};
struct patchConstParam {
float edgeTessFactors[3] : SV_TessFactor;
float insideTessFactor : SV_InsideTessFactor;
// PN-Triangles計算用のコントロールポイント
float3 b111 : TEXCOORD0;
float3 positionsOS[3][3] : TEXCOORD1;
};
struct d2f {
float4 positionCS : SV_POSITION;
float2 uv : TEXCOORD0;
float3 initNormalOS : NORMAL;
float3 initNormalWS : TEXCOORD1;
float3 positionOS : TEXCOORD2;
float3 initPositionOS : TEXCOORD3;
float crackLevel : TEXCOORD4;
};
// ---------------------------------------------------------------------------------------
// メソッド
// ---------------------------------------------------------------------------------------
/**
* Xorshift32を用いて32bitの擬似乱数を生成する
*/
uint Xorshift32(uint value) {
value = value ^ (value << 13);
value = value ^ (value >> 17);
value = value ^ (value << 5);
return value;
}
/**
* 整数の値を1未満の小数にマッピングする
*/
float MapToFloat(uint value) {
const float precion = 100000000.0;
return (value % precion) * rcp(precion);
}
/**
* 3次元のランダムな値を算出する
*/
float3 Random3(uint3 src, int seed) {
uint3 random;
random.x = Xorshift32(mad(src.x, src.y, src.z));
random.y = Xorshift32(mad(random.x, src.z, src.x) + seed);
random.z = Xorshift32(mad(random.y, src.x, src.y) + seed);
random.x = Xorshift32(mad(random.z, src.y, src.z) + seed);
return float3(MapToFloat(random.x), MapToFloat(random.y), MapToFloat(random.z));
}
/**
* 指定した座標に対して、ボロノイパターンの最も近いランダム点と、2番目に近いランダム点を取得する
*/
void CreateVoronoi(float3 pos, out float3 closest, out float3 secondClosest, out float secondDistance) {
// セル番号が負の値とならないようにオフセット加算
const uint offset = 100;
uint3 cellIdx;
float3 reminders = modf(pos + offset, cellIdx);
// 対象地点が所属するセルと隣接するセル全てに対してランダム点との距離をチェックし
// 1番近い点と2番目に近い点を見付ける
float2 closestDistances = 8.0;
[unroll]
for(int i = -1; i <= 1; i++)
[unroll]
for(int j = -1; j <= 1; j++)
[unroll]
for(int k = -1; k <= 1; k++) {
int3 neighborIdx = int3(i, j, k);
// そのセル内でのランダム点の相対位置を取得
float3 randomPos = Random3(cellIdx + neighborIdx, _RandomSeed);
// 対象地点からランダム点に向かうベクトル
float3 vec = randomPos + float3(neighborIdx) - reminders;
// 距離は全て二乗で比較
float distance = dot(vec, vec);
if (distance < closestDistances.x) {
closestDistances.y = closestDistances.x;
closestDistances.x = distance;
secondClosest = closest;
closest = vec;
} else if (distance < closestDistances.y) {
closestDistances.y = distance;
secondClosest = vec;
}
}
secondDistance = closestDistances.y;
}
/**
* 指定した座標がボロノイ図の境界線となるかどうかを0~1で返す
*/
float GetVoronoiBorder(float3 pos, out float secondDistance) {
float3 a, b;
CreateVoronoi(pos, a, b, secondDistance);
/*
* 以下のベクトルの内積が境界線までの距離となる
* ・対象地点から、1番近いランダム点と2番目に近い点の中点に向かうベクトル
* ・1番近い点と2番目に近い点を結ぶ線の単位ベクトル
*/
float distance = dot(0.5 * (a + b), normalize(b - a));
return 1.0 - smoothstep(_CrackWidth, _CrackWidth + _CrackWallWidth, distance);
}
/**
* 指定した座標のひび度合いを0~1で返す
*/
float GetCrackLevel(float3 pos) {
// ボロノイ図の境界線で擬似的なひび模様を表現
float secondDistance;
float level = GetVoronoiBorder(pos * _CrackDetailedness, secondDistance);
/*
* 部分的にひびを消すためにノイズを追加
* 計算量が少なくて済むようにボロノイのF2(2番目に近い点との距離)を利用する
* 距離が一定値以下の場合はひび対象から外す
*/
float f2Factor = 1.0 - sin(_CrackProgress * PI * 0.5);
float minTh = (2.9 * f2Factor);
float maxTh = (3.5 * f2Factor);
float factor = smoothstep(minTh, maxTh, secondDistance * 2.0);
level *= factor;
return level;
}
/**
* ひびが入った後の座標を計算する
*/
float3 CalcCrackedPos(float3 localPos, float3 localNormal, float3 worldNormal, out float crackLevel) {
crackLevel = (_CrackProgress == 0 || dot(worldNormal, GetViewForwardDir()) > 0.5) ? 0.0 : GetCrackLevel(localPos);
// ひび対象の場合は法線と逆方向に凹ませる
float depth = crackLevel * _CrackDepth;
localPos -= localNormal * depth;
return localPos;
}
/**
* [パッチ定数関数用]
* PN-Triangles用のコントロールポイントを算出する
*/
float3 CalcControlPointForPnTri(float3 posA, float3 posB, float3 normalA) {
// PosAとPosBを結ぶ線分を1:2に分けた地点をPosAの接平面上に移動した座標を算出
return (2.0 * posA + posB - (dot((posB - posA), normalA) * normalA)) * OneThird;
}
/**
* [パッチ定数関数用]
* PN-TrianglesのB111の位置を計算する
*
* 参考:https://alex.vlachos.com/graphics/CurvedPNTriangles.pdf
*/
float3 CalcPnTriB111Pos(float3 controlPoints[3][3]) {
float3 b300 = controlPoints[0][0];
float3 b210 = controlPoints[0][1];
float3 b120 = controlPoints[0][2];
float3 b030 = controlPoints[1][0];
float3 b021 = controlPoints[1][1];
float3 b012 = controlPoints[1][2];
float3 b003 = controlPoints[2][0];
float3 b102 = controlPoints[2][1];
float3 b201 = controlPoints[2][2];
float3 e = (b210 + b120 + b021 + b012 + b102 + b201) * OneSixth;
float3 v = (b003 + b030 + b300) * OneThird;
return e + ((e - v) * 0.5);
}
/**
* [ドメインシェーダー用]
* OutputTopology:triangle_cwで生成された重心座標系の座標をsrcの空間の座標に換算する
*/
float3 CalcSubdividedPos(float3 src[3], float3 baryCentricCoords) {
return src[0] * baryCentricCoords.x + src[1] * baryCentricCoords.y + src[2] * baryCentricCoords.z;
}
/**
* [ドメインシェーダー用]
* PN-Trianglesを用いてカーブ上になるように変位させた座標を算出する
*
* 以下を参考にした
* - PN-Trianglesの理論
* https://alex.vlachos.com/graphics/CurvedPNTriangles.pdf
* - 実装(PN-Triangles-AENの実装ではあるが、PN-Trianglesとの共通部分も多い)
* https://developer.download.nvidia.com/whitepapers/2010/PN-AEN-Triangles-Whitepaper.pdf
*/
float3 CalcPnTriPosition(float3 controlPoints[3][3], float3 b111, float3 baryCentricCoords) {
float u = baryCentricCoords.x;
float v = baryCentricCoords.y;
float w = baryCentricCoords.z;
float uu = u * u;
float vv = v * v;
float ww = w * w;
float uu3 = 3.0 * uu;
float vv3 = 3.0 * vv;
float ww3 = 3.0 * ww;
return controlPoints[0][0] * u * uu
+ controlPoints[1][0] * v * vv
+ controlPoints[2][0] * w * ww
+ controlPoints[0][1] * uu3 * v
+ controlPoints[0][2] * vv3 * u
+ controlPoints[1][1] * vv3 * w
+ controlPoints[1][2] * ww3 * v
+ controlPoints[2][1] * ww3 * u
+ controlPoints[2][2] * uu3 * w
+ b111 * 6.0 * w * u * v;
}
/**
* [フラグメントシェーダー用]
* CrackLevelに応じたOcclusionを算出する
*/
half CalcOcclusion(float crackLevel) {
// ひびの深さに応じて影を濃くする
half occlusion = pow(lerp(1.0, 0.9, crackLevel), 2.0);
// ひびが深い部分で、隣接ピクセルの高低差が大きい場合は影を濃くする
occlusion *= (crackLevel > 0.95 ? lerp(0.9, 1.0, 1.0 - smoothstep(0.0, 0.1, max(abs(ddy(crackLevel)), abs(ddx(crackLevel))))) : 1.0);
return occlusion;
}
// ---------------------------------------------------------------------------------------
// シェーダー関数
// ---------------------------------------------------------------------------------------
/**
* 頂点シェーダー
*/
v2d Vert(Attributes input) {
v2d output;
output.positionOS = input.positionOS;
output.normalOS = input.normalOS;
Varyings varyings = LitPassVertex(input);
output.uv = varyings.uv;
output.normalWS = varyings.normalWS;
return output;
}
/**
* メインハルシェーダー
*/
[domain("tri")]
[partitioning("integer")]
[outputtopology("triangle_cw")]
[outputcontrolpoints(3)]
[patchconstantfunc("PatchConstantFunc")]
v2d Hull(InputPatch<v2d, 3> inputs, uint id:SV_OutputControlPointID) {
v2d output = inputs[id];
return output;
}
/**
* パッチ定数関数
*/
patchConstParam PatchConstantFunc(InputPatch<v2d, 3> inputs) {
patchConstParam output;
int subdividingCount = (_CrackProgress == 0.0 || _SubdividingCount <= 1) ? 0 : _SubdividingCount;
[unroll]
for (uint i = 0; i < 3; i++) {
// カメラを向いていない面は分割しない
subdividingCount = subdividingCount > 0 && dot(inputs[i].normalWS, GetViewForwardDir()) <= 0.5 ? subdividingCount : 0;
}
// プロパティ設定に合う分割数算出
float3 rawEdgeFactors = subdividingCount;
float3 roundedEdgeTessFactors;
float roundedInsideTessFactor;
float unroundedInsideTessFactor;
ProcessTriTessFactorsAvg(rawEdgeFactors, _SubdividingInsideScaleFactor, roundedEdgeTessFactors, roundedInsideTessFactor, unroundedInsideTessFactor);
// 辺側、内側それぞれの分割数を指定
output.edgeTessFactors[0] = roundedEdgeTessFactors.x;
output.edgeTessFactors[1] = roundedEdgeTessFactors.y;
output.edgeTessFactors[2] = roundedEdgeTessFactors.z;
output.insideTessFactor = roundedInsideTessFactor;
// PN-Triangles計算用のコントロールポイント算出
bool usesPnTriangles = _PnTriFactor > 0.0 && subdividingCount > 1;
[unroll]
for (i = 0; i < 3; i++) {
uint nextId = (i + 1) % 3;
output.positionsOS[i][0] = inputs[i].positionOS.xyz;
if (usesPnTriangles) {
output.positionsOS[i][1]
= CalcControlPointForPnTri(inputs[i].positionOS.xyz, inputs[nextId].positionOS.xyz, inputs[i].normalOS);
output.positionsOS[i][2]
= CalcControlPointForPnTri(inputs[nextId].positionOS.xyz, inputs[i].positionOS.xyz, inputs[nextId].normalOS);
} else {
output.positionsOS[i][1] = 0.0;
output.positionsOS[i][2] = 0.0;
}
}
output.b111 = usesPnTriangles ? CalcPnTriB111Pos(output.positionsOS) : 0.0;
return output;
}
/**
* ドメインシェーダー
*/
[domain("tri")]
d2f Domain(patchConstParam param, const OutputPatch<v2d, 3> inputs, float3 baryCentricCoords:SV_DomainLocation) {
d2f output;
// まずはフラットなポリゴン上に算出された座標を求める
// 算出された座標を重心座標系からローカル座標等に換算
float3 srcLocalPositions[3];
float3 srcLocalNormals[3];
float3 srcUVs[3];
float3 srcWorldTangents[3];
[unroll]
for (uint i = 0; i < 3; i++) {
srcLocalPositions[i] = inputs[i].positionOS.xyz;
srcLocalNormals[i] = inputs[i].normalOS;
srcUVs[i] = float3(inputs[i].uv, 0.0);
}
float3 flatLocalPos = CalcSubdividedPos(srcLocalPositions, baryCentricCoords);
output.uv = CalcSubdividedPos(srcUVs, baryCentricCoords).xy;
// 法線についてはPN-Trianglesで計算するとひび用の頂点移動時に亀裂が発生しやすくなるので、フラットなポリゴンの法線を採用
float3 localNormal = CalcSubdividedPos(srcLocalNormals, baryCentricCoords);
output.initNormalOS = localNormal;
output.initNormalWS = TransformObjectToWorldNormal(localNormal);
// PN-Trianglesを適用すると亀裂が発生する場合はポリゴンの辺上の頂点は変位させない
// (重心座標系では頂点から向かいの辺に向かって座標が1→0と変化することを利用)
bool isOnSides = min(min(baryCentricCoords.x, baryCentricCoords.y), baryCentricCoords.z) == 0;
if (_PnTriFactor == 0.0 || (!_AdaptsPolygonEdgeToPnTri && isOnSides)) {
output.initPositionOS = flatLocalPos;
} else {
// PN-Trianglesを用いてカーブ上になるように座標変位
float3 pnTriLocalPos = CalcPnTriPosition(param.positionsOS, param.b111, baryCentricCoords);
output.initPositionOS = lerp(flatLocalPos, pnTriLocalPos, _PnTriFactor);
}
// 頂点がひび模様に重なる場合は凹ませる
output.positionOS = CalcCrackedPos(output.initPositionOS, output.initNormalOS, output.initNormalWS, output.crackLevel);
output.positionCS = TransformObjectToHClip(output.positionOS);
return output;
}
/**
* フラグメントシェーダー
*/
half4 Frag(d2f input) : SV_Target {
float crackLevel = input.crackLevel;
float3 positionOS = _DrawsCrackWithPixelUnit ? CalcCrackedPos(input.initPositionOS, input.initNormalOS, input.initNormalWS, crackLevel) : input.positionOS;
float3 positionWS = TransformObjectToWorld(positionOS);
// 隣接のピクセルとのワールド座標の差分を取得後に外積を求めて法線算出
float3 normalWS = crackLevel > 0.0 ? normalize(cross(ddy(positionWS), ddx(positionWS))) : input.initNormalWS;
Varyings varyings = (Varyings)0;
varyings.positionCS = input.positionCS;
varyings.uv = input.uv;
varyings.positionWS = positionWS;
varyings.normalWS = normalWS;
SurfaceData surfaceData;
InitializeStandardLitSurfaceData(input.uv, surfaceData);
OUTPUT_SH(normalWS, varyings.vertexSH);
InputData inputData;
InitializeInputData(varyings, surfaceData.normalTS, inputData);
inputData.normalWS = crackLevel > 0.0 ? normalWS : inputData.normalWS;
inputData.vertexLighting = VertexLighting(positionWS, inputData.normalWS);
/* ひび模様 */
// ひび対象の場合はクラックカラーを追加
surfaceData.albedo = lerp(surfaceData.albedo, _CrackColor.rgb, crackLevel);
// ひび部分はAO設定
surfaceData.occlusion = min(surfaceData.occlusion, CalcOcclusion(crackLevel));
half4 color = UniversalFragmentPBR(inputData, surfaceData);
clip(color.a <= 0 ? -1 : 1);
return color;
}
ENDHLSL
}
}
FallBack "Universal Render Pipeline/Lit"
}
まとめ
これまでのひび入れシェーダーでは、モデルによってはひび部分を凹ませたときにクラックが発生することがあったので、緩和する方法は無いかとPN-Trianglesを試してみました。
シェーダーパラメータでモデルに合った設定を探すことにより、ある程度はクラックを避けることはできそうです。
PN-Triangles自体の感触としては、処理がかなり複雑になり可読性やパフォーマンスへの影響が懸念される割に効果を感じにくいため、グラフィックに余裕がある環境において有効活用できる手法なのだろうなと思いました。
次は法線マップ等にも対応させた最終形のコードについてです。