概要
画像分析の際、HSV色空間を使うことは多いと思います。特に H(色相)と S(彩度)を散布図にプロットすると、画像の色彩の特徴をよく捉えることができます。
ただ、H と S は局座標空間のパラメータです。このため、H は 0〜360度(OpenCV では 0〜180)の位相角となります。ここで問題があります。H が 0付近と、H が 360付近は 同じような色相を表すことになってしまいます。値が大きく違うのに特性はよく似ている、というのは好ましくありません。機械学習他、数理統計処理を行うには、工夫が必要でしょう。
そこで、局座標から直交座標に変換すれば、うまく処理ができると思います。ちょっと試してみました。
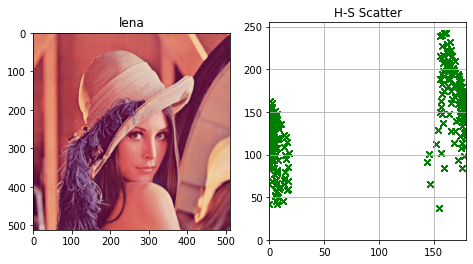
HSV色空間:H と S の散布図
試しに、赤っぽい( H が 0付近、及び OpenCV の180 付近の値をとる点が多い)画像について調べてみます。サンプルは lena にしてみましょう。
必要なライブラリをインポートします。
import cv2
from matplotlib import pyplot as plt
lena を読み込んで、OpenCVで読み込んだBGR形式の画像をHSV変換します。
#matplotlib でも表示するため、合わせてRGB形式も作っておきます。
lena_bgr = cv2.imread('lena.png')
lena_hsv = cv2.cvtColor(lena_bgr,cv2.COLOR_BGR2HSV)
lena_rgb = cv2.cvtColor(lena_bgr,cv2.COLOR_BGR2RGB)
画像の色彩の特性を見るため、横軸H、縦軸S として散布図を作ってみます。
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
plt.imshow(lena_rgb)
plt.subplot(1,3,2)
plt.xlim(0,180)
plt.ylim(0,255)
plt.grid()
plt.scatter(x=lena_hsv[:,:,0],y=lena_hsv[:,:,1],alpha=0.01,marker='x',color='g')
plt.show()
彩度は広い範囲に分布していますが、色相は 0付近、あるいは180付近に偏っています。lena が赤っぽい画像であることをよく示しています。
ただ「赤っぽい」のだから散布図上の点が二つのグループに分かれることはちょっと混乱を招きますね。SVM 他の機械学習をする際も、あまり都合がよくないかもしれません。そこで、これを直交座標系で表すことを考えます。
直交座標系による色彩の表現
直交座標系に変換するのは難しくはありません。H(色相)が位相、S(彩度)が絶対値なので、
\begin{align}
x = S\,\cos(\,H\,)\\
\\y = S\,\sin(\,H\,)
\end{align}
これで求めることができますね。
注意が必要なのは、OpenCV では H(色相)を0〜360でなく、0〜179 で取り扱っている点でしょう。計算する際は、H の値を2倍にしないといけません。
# 8ビットの符号なし整数では、255までしか表せないですから便宜上ですね
また、numpy の三角関数は単位にラジアンを使っているので、そこも気をつけてください。
では、直交座標系に変換してみます。
lena_temp = lena_hsv.astype(np.float32)
lena_xyv = np.zeros(lena_hsv.shape).astype(np.float32)
# 位相の単位をラジアンに変換
# x = cos((2*H) * 2pi / 360) = cos(H * pi / 90)
# y = sin((2*H) * 2pi / 360) = sin(H * pi / 90)
lena_xyv[:,:,0] = lena_temp[:,:,1] * np.cos(lena_temp[:,:,0]*(np.pi)/90)
lena_xyv[:,:,1] = lena_temp[:,:,1] * np.sin(lena_temp[:,:,0]*(np.pi)/90)
lena_xyv[:,:,2] = lena_hsv[:,:,2]
sin, cos は実数計算となりますので、float32 に型変換したインスタンスを作って作業してます。
また、明度 V はここでは使いませんが、念の為、保存しておきました。
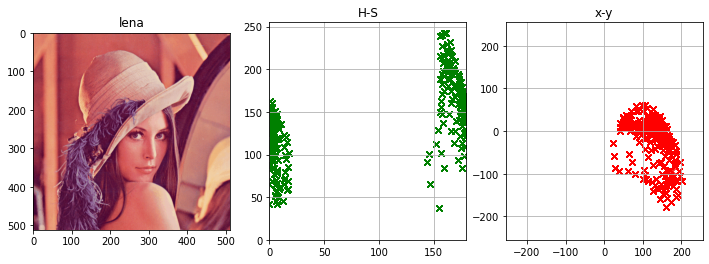
結果比較
先程のように元画像と H-S の散布図、それに今回直交座標変換した x-y の散布図を並べてみます。
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
plt.title('lena')
plt.imshow(lena_rgb)
plt.subplot(1,3,2)
plt.title('H-S')
plt.xlim(0,180)
plt.ylim(0,255)
plt.grid()
plt.scatter(x=lena_hsv[:,:,0],y=lena_hsv[:,:,1],alpha=0.2)
plt.subplot(1,3,3)
plt.title('x-y')
plt.xlim(-255,255)
plt.ylim(-255,255)
plt.grid()
plt.scatter(x=lena_xyv[:,:,0],y=lena_xyv[:,:,1],alpha=0.01,marker='x',color='r')
plt.show()
直交座標系で見ると、赤っぽい lena が ひとかたまりになっててよりよく特徴を表してるようです。
色相、彩度を使って機械学習する際には、直交座標系で考えるとうまくいく場合も多いんじゃないでしょうか。