ナンバープレースを初めて触るPythonで無理やりに解く

---

この記事は株式会社LIGのアドベントカレンダー2017、14日目の記事です。

---

背景

Pythonに触りたい僕の前で、義母がナンバープレースに取り組んでいた。

ナンバープレースのルール

1	2	3	4	5	6	7	8	9
4	5	6	7	8	9	1	2	3
7	8	9	1	2	3	4	5	6
2	1	4	3	6	5	8	9	7
3	6	5	8	9	7	2	1	4
8	9	7	2	1	4	3	6	5
5	3	1	6	4	2	9	7	8
6	4	2	9	7	8	5	**?**	1
9	7	8	5	3	1	6	4	2

ナンバープレース、または数独（株式会社ニコリの登録商標）はルールにそって上記のような表を数字で埋めていくパズルの一種。様々な形やローカルルールがあるが9*9の標準的なルールは下記の通り。

1. 縦を1〜９の重複しない値で埋める。
2. 横を1〜９の重複しない値で埋める。
3. エリアを1〜９の重複しない値で埋める。

エリアは上記表だと分かりにくいが9*9のテーブル上に存在する３*３の表のことで、9*9上のテーブルには左上から９つエリアが存在する。ルールに沿って考えると、**?**の部分には３が入る。ルール詳細についてはwikiをご確認ください。

ナンバープレースはシンプルなルール故に、ロジック的にかなり素直に解けるはずである。たぶん二次元配列で再帰を使えば何とかなんだろ、ただ計算量は膨大になりそうだ、ってずっと前から思ってたけど、じゃあいざ作るかっていうとわざわざ作ることはない。今回はアドベントカレンダーということで、あまり触ったことないPythonの初めての課題にちょうどよさそうということでチャレンジする。

そういう意味でまずPythonのシンタックスからしておぼろげなので、そのお家芸であるAIやら機械学習やらは使用しないというか使用できない。それ以前の課題、ロジックの遊びとしてお付き合いください。

ナンバープレースを解く考え方

素直に考えると以下の手順で解けるだろう。

1. ナンプレ用の二次元配列のテーブルを作る。
2. 既に与えられている入力値によって必然的に確定される数値を埋められるだけ埋める。
3. 埋められない箇所へ仮に値を入力して、齟齬が発生しないか確認する。
4. 2,3を繰り返して値を埋めていく。
5. 論理的に埋められない値が出た場合、3の仮定が間違っているので、その時点へ戻って別の値を当てはめていく。

なお、本稿では基本的に9*9の標準的なナンバープレースを解くものとする。皆さんもナンプレ、ずっと気になっていたと思う。皆さんの良い暇つぶしになりますように。何も冴えた方法を使ってないと思うので、お時間あれば、より綺麗でより速い、皆さんのナンプレ解法教えて下さい。

ナンバープレースを解くコードを書く

github.com/masakuni-ito/number-place

import sys
import copy
import math
from pprint import pprint

class NumberPlace:

    @property
    def debug(self):
        return self._table

    @property
    def table(self):
        return self._table

    def __init__(self, max_number=9, debug=False):
        self._debug = debug
        self._table = []
        self._has_area_check = False
        self._area_length = 0
        self._depth = 0

        # 初期化
        tmp_table = []
        for row_num in range(0, max_number):

            row = []
            for col_num in range(0, max_number):
                row.append(0)

            tmp_table.append(row)

        self._table = tmp_table

        # エリアでのチェック行えるか
        # 平方根が自然数であること
        # max_number=4, 9, 16, 25...
        sqrt_num = math.sqrt(max_number)
        int_sqrt_num = math.floor(sqrt_num)
        if sqrt_num == int_sqrt_num:
            self._has_area_check = True
            self._area_length = int_sqrt_num

    def new_table(self, max_number=9):
        # 初期化
        tmp_table = []
        for row_num in range(0, max_number):

            row = []
            for col_num in range(0, max_number):
                row.append(0)

            tmp_table.append(row)

        return tmp_table

    def set_table(self, table):
        self._table = []
        self._has_area_check = False
        self._area_length = 0
        self._depth = 0

        # 受け入れられるのはx*xの二次元配列のみ
        if not isinstance(table, list) or len(table) <= 0:
            raise Exception('invalid table: this table is not list.')

        max_number = len(table)

        # 縦横同一の長さ
        for row in table:
            if not isinstance(row, list) or len(row) != max_number:
                raise Exception('invalid table: this row is not list or misshapen square.')

        # 数値以外は受け入れない
        for row_num in range(0, max_number):
            for col_num in range(0, max_number):
                if not isinstance(table[row_num][col_num], int):
                    raise Exception('invalid table: invalid values.')

        # エリアでのチェック行えるか
        # 平方根が自然数であること
        # max_number=4, 9, 16, 25...
        sqrt_num = math.sqrt(max_number)
        int_sqrt_num = math.floor(sqrt_num)
        if sqrt_num == int_sqrt_num:
            self._has_area_check = True
            self._area_length = int_sqrt_num

        # 初期値確認
        self.__validate_table(table)

        self._table = copy.deepcopy(table)

    def __validate_table(self, table):
        
        max_number = self.__get_max_number(table)

        for row_num in range(0, max_number):
            for col_num in range(0, max_number):

                # 横マスの現状入力値
                row = self.__get_row_numbers(table, row_num)

                # 既に不整合が起きている
                for i in range(1, max_number+1):
                    if row.count(i) >= 2:
                        raise Exception('invalid table: The value already entered is incorrect.')

                # 縦マスの現状入力値
                col = self.__get_col_numbers(table, col_num)

                # 既に不整合が起きている
                for i in range(1, max_number+1):
                    if col.count(i) >= 2:
                        raise Exception('invalid table: The value already entered is incorrect.')

                # エリアでのチェックが必要かどうか
                if self._has_area_check:
                    area = self.__get_area_numbers(table, row_num, col_num)

                    # 既に不整合が起きている
                    for i in range(1, max_number+1):
                        if area.count(i) >= 2:
                            raise Exception('invalid table: The value already entered is incorrect.')

        return True

    def __get_max_number(self, table):
        return len(table)

    def __get_row_numbers(self, table, row_num):
        return table[row_num]

    def __get_col_numbers(self, table, col_num):
        col = []

        max_number = self.__get_max_number(table)
        for i in range(0, max_number):
            col.append(table[i][col_num])

        return col

    def __get_area_numbers(self, table, row_num, col_num):
        area = []
        
        # 現在マスが属するエリアの最小値位置を求めて基点とする
        base_point_row = math.floor(row_num / self._area_length) * self._area_length
        base_point_col = math.floor(col_num / self._area_length) * self._area_length
        
        # 現在のエリアに存在する入力値を取得する
        for area_row_num in range(base_point_row, base_point_row + self._area_length):
            for area_col_num in range(base_point_col, base_point_col + self._area_length):
                area.append(table[area_row_num][area_col_num])

        return area

    def fill(self, table=None):

        if table is None:
            table = copy.deepcopy(self._table)

        filled_table = self.__recursive_fill(table)

        if filled_table == False: return False

        self._table = filled_table

        return True

    def __recursive_fill(self, table):

        print('|' * (self._depth + 1))

        # 現状入力されている値から、入力できる値を入れ込む
        if self._debug: pprint(">>> fixed")
        table = self.__fix(copy.deepcopy(table))
        if self._debug: pprint(table)
        if self._debug: pprint("<<< fixed")

        # 一つ一つ入力して齟齬が発生しないか確かめる
        max_number = self.__get_max_number(table)
        for row_num in range(0, max_number):
            for col_num in range(0, max_number):

                # 既に入っているものに対しては走査しない
                if table[row_num][col_num] != 0:
                    continue

                if self._debug: pprint("row: {0}, col: {1}".format(row_num, col_num))
                suspicious_numbers = self.__get_suspicious_numbers(table, row_num, col_num)

                # このマスに当てはまるものがないため、前提のマスが誤っている
                if suspicious_numbers == False:
                    if self._debug: pprint("suspicious_numbers is False")
                    return False

                right_number = False
                for suspicious_number in suspicious_numbers:

                    # 仮に入れ込んで走査する
                    tmp_table = copy.deepcopy(table)
                    tmp_table[row_num][col_num] = suspicious_number

                    self._depth += 1

                    if self._debug: pprint(">>> try row: {0}, col: {1}, try: {2} of {3}".format(row_num, col_num, suspicious_number, suspicious_numbers))
                    if self._debug: pprint(tmp_table)
                    filled_table = self.__recursive_fill(tmp_table)
                    if self._debug: pprint("<<< try row: {0}, col: {1}, try: {2} of {3}".format(row_num, col_num, suspicious_number, suspicious_numbers))

                    self._depth -= 1

                    # このマスに suspicious_number を入れると再帰先で齟齬が起きる
                    if filled_table == False:
                        continue

                    if self._debug: pprint(">>> result")
                    if self._debug: pprint(filled_table)
                    if self._debug: pprint("<<< result")

                    # 入れ込んだ結果、現時点で誤りが出ていないので正当な値と仮に決定する
                    table = filled_table

                    # 再帰先でも齟齬は起きなかった
                    right_number = True
                    break

                # 走査してみた結果、再帰先のマスで齟齬が生まれるため、
                # この suspicious_numbers は使えず、前提のマスが誤っている
                if right_number == False:
                    return False

        print('|' * (self._depth + 1))
        return table

    def __fix(self, table):

        max_number = self.__get_max_number(table)

        while True:
            changed = False
            for row_num in range(0, max_number):
                for col_num in range(0, max_number):

            
                    # 既に入っているものに対しては走査しない
                    if table[row_num][col_num] != 0:
                        continue

                    # row_num, col_numにおいて、一つに確定できる数を求める
                    fixed_number = self.__get_fixed_number(table, row_num, col_num)

                    if fixed_number == False:
                        continue

                    table[row_num][col_num] = fixed_number
                    changed = True

            # 一つでも入力値に変動があったらループ
            if changed == False:
                break

        return table

    def __get_fixed_number(self, table, row_num, col_num):

        suspicious_numbers = self.__get_suspicious_numbers(table, row_num, col_num)
        if suspicious_numbers == False or len(suspicious_numbers) != 1:
            return False

        # 入力値が一つに確定できた
        fix_num = suspicious_numbers.pop()
        if self._debug: pprint("row: {0}, col: {1}, fix: {2}".format(row_num, col_num, fix_num))

        return fix_num

    def __get_suspicious_numbers(self, table, row_num, col_num):

        max_number = self.__get_max_number(table)

        # 横マスの現状入力値
        row = self.__get_row_numbers(table, row_num)

        # 横マスで入力可能な入力値
        allow_row_numbers = []
        for i in range(1, max_number+1):
            if i not in row:
                allow_row_numbers.append(i)

        # 縦マスの現状入力値
        col = self.__get_col_numbers(table, col_num)

        # 縦マスで入力可能な入力値
        allow_col_numbers = []
        for i in range(1, max_number+1):
            if i not in col:
                allow_col_numbers.append(i)
 
        # エリアでのチェックが必要かどうか
        allow_area_numbers = []
        if self._has_area_check:

            # エリアマスの現状入力値
            area = self.__get_area_numbers(table, row_num, col_num)

            # エリアマスで入力可能な入力値
            for i in range(1, max_number+1):
                if i not in area:
                    allow_area_numbers.append(i)
        else:
            # エリアマスでのチェックが不要であれば、エリアマスとしては全てを許容する
            for i in range(1, max_number+1):
                allow_area_numbers.append(i)

        # 横マスで入力可能なものは、少なくとも一つ以上は他でも入力可能である必要がある
        found = False
        for num in allow_row_numbers:
            if num in allow_col_numbers and num in allow_area_numbers:
                found = True
                break

        if found == False:
            return False

        # 縦マスで入力可能なものは、少なくとも一つ以上は他でも入力可能である必要がある
        found = False
        for num in allow_col_numbers:
            if num in allow_row_numbers and num in allow_area_numbers:
                found = True
                break

        if found == False:
            return False

        # エリアで入力可能なものは、少なくとも一つ以上は他でも入力可能である必要がある
        found = False
        for num in allow_area_numbers:
            if num in allow_row_numbers and num in allow_col_numbers:
                found = True
                break

        if found == False:
            return False

        # 全てに共通して入力可能な値しか入力はできないため抽出する
        suspicious_numbers = []
        for i in range(1, max_number+1):
            if i in allow_row_numbers and i in allow_col_numbers and i in allow_area_numbers:
                suspicious_numbers.append(i)

        return suspicious_numbers

def main():
    number_place = NumberPlace()

    # set table
    table = number_place.new_table(9)
    #table = [
    #    [0, 0, 0, 0, 0, 0, 0],
    #    [0, 0, 0, 0, 0, 0, 0],
    #    [0, 0, 0, 0, 0, 0, 0],
    #    [0, 0, 0, 0, 0, 0, 0],
    #    [0, 0, 0, 0, 0, 0, 0],
    #    [0, 0, 0, 0, 0, 0, 0],
    #    [0, 0, 0, 0, 0, 0, 0]
    #]
    number_place.set_table(table)

    number_place.fill()
    pprint(number_place.table)

if __name__ == '__main__':
    main()

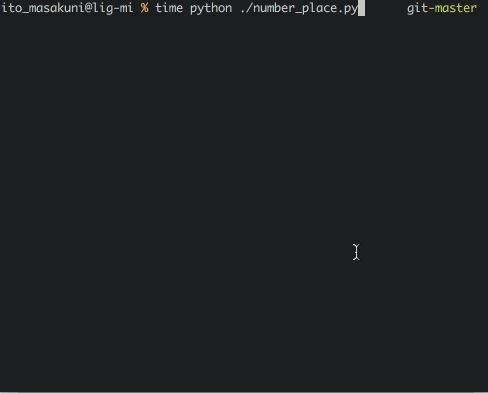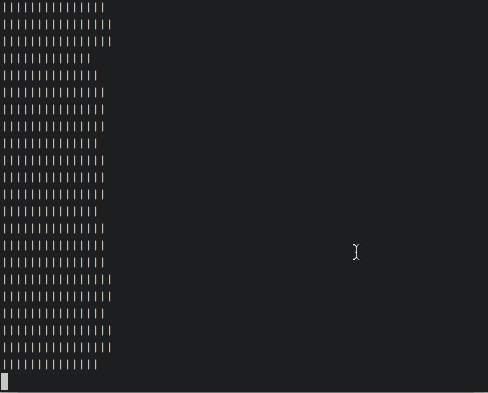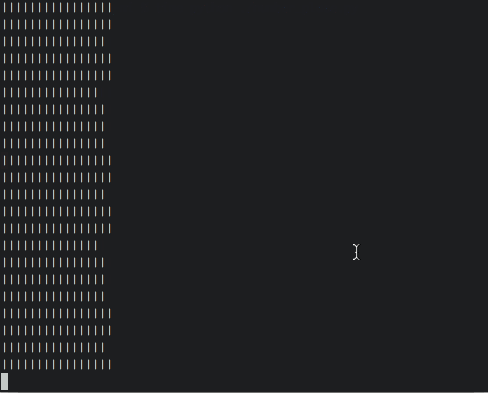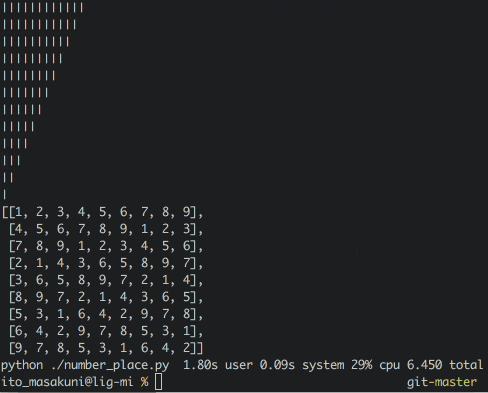
ナンバープレースを解く

出来上がったのが上記のテーブルで、行、列、エリア共にそれぞれ１〜９が入っていて誤りはなさそう。再帰は上手く動くと気持ちがいい。

反省と課題

• PHP脳で取り組んで、deepcopyの部分で相当ハマった。
• デバッグがどうすればいいのか分からなくて何だか不便だ。
• 9*9以上のサイズを埋めようとすると相応の時間がかかる。MacBookPro 16Gで12*12が47.59sかかった。今はたぶん仮に入力した一つ目の値が正しいかどうか最後まで分からないので、初期値として齟齬が起きない程度に適当な値を入力してから取り組んだ方が早く解けるだろう。
• Pythonらしい記法を一切使ってない気がするし、合ってるかどうかも自信がない。少なくともPythonを使ったメリットは全くなかった。**後で気づいたけど、わざわざPythonならNumPyを使うべき。**2018年はもっとPythonに触れていくというところで、2017年もお世話になりました。

最後に

妻に「ついに俺は一瞬で解けるようになってしまった」と宣言したら、「じゃあ何が面白いの？」と冷たい目をされた。