本記事は、Processing Advent Calendar 2024用の記事です。
授業用の資料を一部抜粋して記事にしました。
ネットワークとは?
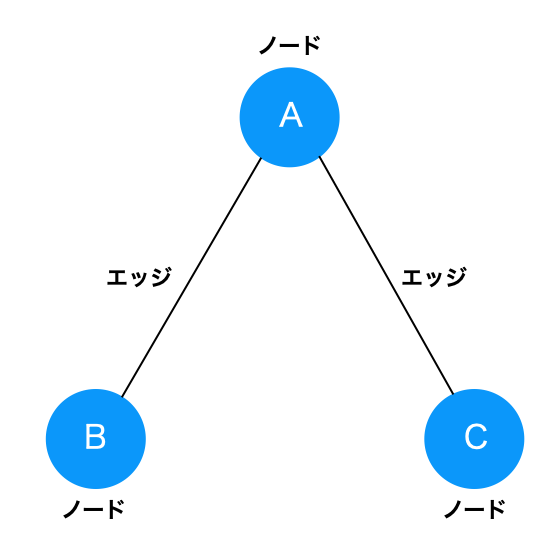
ネットワークとは、簡単に言えば2つ以上の対象とその対象同士の関係からなる構造です。例えば、オフィスにいるA,B,Cの三人を1時間観察し、どの程度会話したかを観察したとします。
AさんとBさんが会話し、AさんとCさんが会話し、BさんとCさんは全く会話しなかったとしたら、次の図のようなネットワーク構造が得られるでしょう。
対象となるA,B,Cはノードと呼び、円で表されます。それぞれの関係はノード同士を繋ぐエッジと呼ばれる線で表されます。
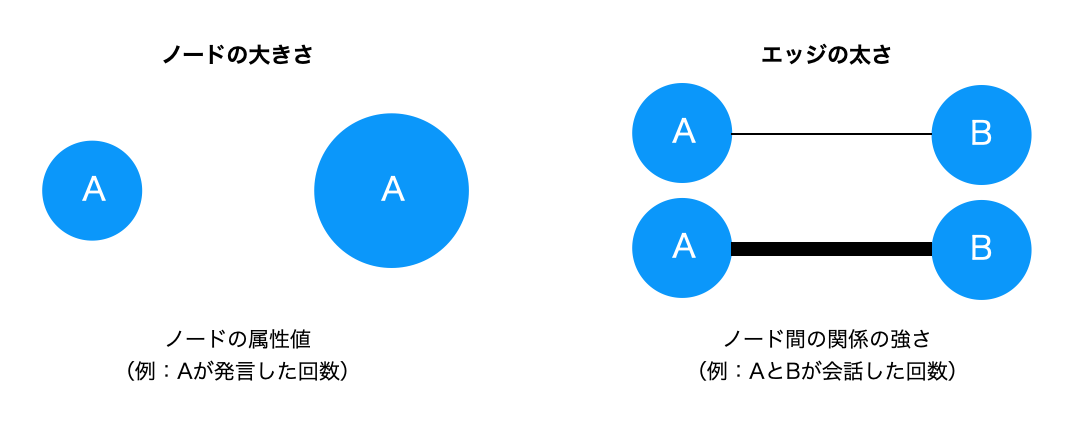
ノードの色や大きさは、ノード固有の属性を示すことができます(例えば発言回数)。エッジの太さはや色は、ノード間の関係の強さ(例えば、会話回数)を示すことができます(図2)
複雑なネットワークを自律的にレイアウトして可視化する
ノードの数やエッジの数が多くなれば構造が複雑になることは想像に難くありません。できるだけ構造を綺麗にビジュアライズするには、ノードが重ならないように一定の距離を保ち交錯するエッジを減らす必要があります。
このような要件を満たすように人間がひとつづつ配置を調整していくのは困難なので、ノードやエッジに物理法則を当てはめて、自律的にレイアウトする力学的アルゴリズムが知られています。
本記事では、この力学的アルゴリズムをProcessingで実装する方法を紹介します。
力学的アルゴリズムの「3つの力」
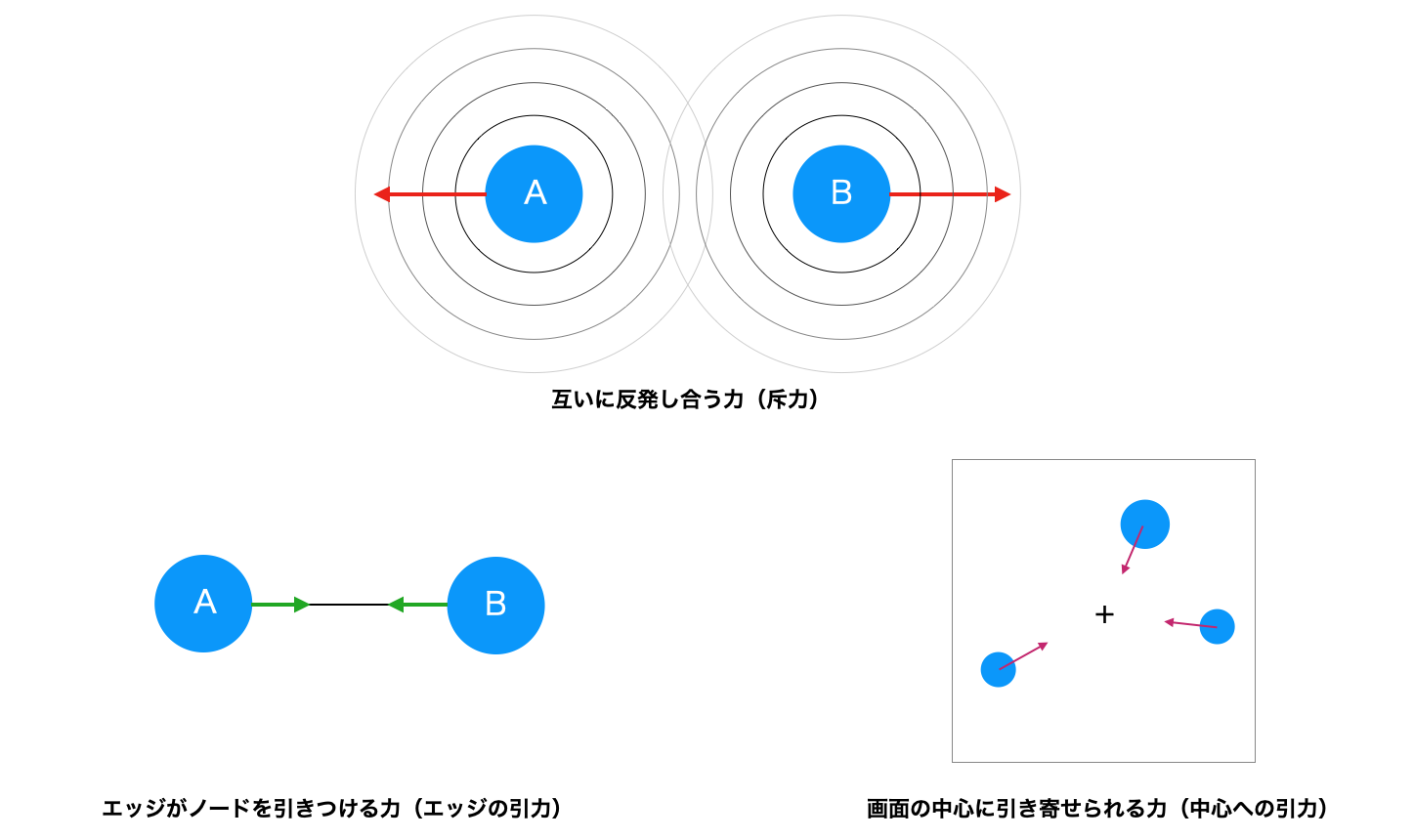
力学的アルゴリズムによってノードやエッジの配置を自動的に決定するには、ノードにかかる次の3つの力(図3)を実装して実行し、力のバランスが拮抗して収束するまで待ちます。また、特定のノードをドラッグして移動できるインタラクションも実装します。
1.ノード同士の反発(斥力)
ひとつ目の力は、ノード同士が反発し遠ざかろうとする力(斥力)です。この力はノード間の距離の2乗に反比例する力で、クーロン力をモデルとしています。ひとつのノードが受ける斥力は、自分を除く他の全てのノードからの斥力を合わせた力になります。これにより、ノード同士の間隔を広げることになります。
2. エッジで結ばれたノードの引力
ふたつ目の力は、エッジで結ばれたノード同士を引きつける力(ノード間の引力)です。この力は、エッジをバネに見立ててエッジが長くなれば引き合う力が強まる「フックの法則」をモデルにしています。これにより、エッジに結ばれたノードが一定の距離まで近づくようになります。
3. ノードを画面中心に引っ張る引力
3つ目の力は、ノードを画面の中心に引きつける力(中心への引力)です。これも、フックの法則を使って、画面の中心に全てのノードを引きつけます。これにより、できるだけネットワーク全体がコンパクトにまとまるようになります。
共起ネットワークを可視化する
本記事では、「共起ネットワーク」と呼ばれる言葉のネットワークを作成します。
共起ネットワークとは
共起ネットワークは、単語や概念がテキスト内で「共起」する関係を視覚化する手法です。「共起」とは、異なる単語が一定の文脈内で同時に現れることを指します。ネットワークでは、ノードが単語を、エッジが単語間の共起関係を表し、その頻度や強さを示します。利点として、データ内の重要な語彙やトピック間の関連性を直感的に把握できる点が挙げられます。具体的な利用シーンとして、検索に用いられる単語の共起関係の可視化や、楽曲の歌詞に出てくるフレーズの共起関係の可視化などがあります。
データの収集
IMDb(Internet Movie Database)に書かれた映画レビュー(英語)データと、それぞれのレビューがポジティブかネガティブかを識別したデータが公開されているので、ポジティブなレビューを100件分取り出して、形容詞同士の共起ペアを生成して上位30件分のペアを収集します。
収集はPythonで行いました。この辺りの説明は割愛しますが、ノートブックを公開しているので、参考にしてください。主な流れは次のとおりです。
- データセットの読み込み
- レビューを100件サンプリング
- レビューから形容詞だけを抽出
- レビューにおける形容詞同士の共起ペアを生成
- レビューの共起ペアそれぞれカウント
- カウントの上位30件のペアに絞ったデータを作成
データはノードの一覧をまとめたcsvとエッジの一覧をまとめたcsvの二つを使用します。
最終的に得られたデータはこちらです。
Processingによる可視化
それでは、このデータを読み込んでProcessingで可視化してみましょう。
アルゴリズムのポイント
まずは、アルゴリズムのポイントをまとめます。
-
データの読み込みと準備
- CSVファイルからノードとエッジの情報を読み込みます。
- ノードのサイズやエッジの重みを取得し、最大値と最小値を計算してスケーリングに利用します。
-
ノードとエッジの初期化
- 各ノードはランダムな位置に配置されます。
- ノードのサイズはCSVファイルのデータから取得し、設定した範囲でスケーリングします。
- エッジは指定されたノード間をつなぎ、その重みもスケーリングされます。
-
物理的な力のシミュレーション
- 斥力(反発力):各ノードは他のノードから距離を保つために反発します。斥力は距離の二乗に反比例して計算されます。
- 中心への引力:各ノードはウィンドウの中心に向かう力を持ち、全体のレイアウトが中央に収束するように働きます。この力はフックの法則に基づいて計算されます。
- エッジの引力:エッジで接続されたノード間には引力が働きます。ノード間の距離が適切になるようにバランスを取ります。
-
描画とユーザーインタラクション
- 各フレームで、ノードとエッジの位置を更新し、それに基づいて描画します。
- マウスでノードをドラッグすることで、そのノードの位置を動かすことができます。
Processingのコード
Node[] nodes;
Edge[] edges;
Node selectedNode = null;
float repulsionForceConstant = 10000; // ノード間の斥力のグローバル変数
float springConstant = 0.01; // ウィンドウ中心に向かうバネ定数のグローバル変数
float attractionForceConstant = 0.01; // ノード間の引力のグローバル変数
float edgeStrokeWeightMax = 8; // エッジの最大太さ
float edgeStrokeWeightMin = 1; // エッジの最小太さ
float edgeWeightMax; // エッジの重みの最大値
float edgeWeightMin; // エッジの重みの最小値
float nodeRadiusMax = 50; // ノードの最大半径
float nodeRadiusMin = 10; // ノードの最小半径
float nodeSizeMax; // ノードのサイズの最大値
float nodeSizeMin; // ノードのサイズの最小値
void setup() {
size(800, 800);
// CSVファイルからノードとエッジをロード
Table nodesTable = loadTable("nodes_positive_cooccurrence_adjectives.csv", "header");
Table edgesTable = loadTable("edges_positive_cooccurrence_adjectives.csv", "header");
// ノードとエッジの配列を初期化
int nodesRowCount = nodesTable.getRowCount();
int edgesRowCount = edgesTable.getRowCount();
nodes = new Node[nodesRowCount];
edges = new Edge[edgesRowCount];
// nodeSizeMaxとnodeSizeMinを極端な値で初期化
nodeSizeMax = Float.MIN_VALUE;
nodeSizeMin = Float.MAX_VALUE;
// nodeSizeMaxとnodeSizeMinを決定するための最初のパス
// ノードのサイズの最大値と最小値を決定する
for (int i = 0; i < nodesRowCount; i++) {
TableRow row = nodesTable.getRow(i);
float size = row.getFloat("size");
if (size > nodeSizeMax) {
nodeSizeMax = size;
}
if (size < nodeSizeMin) {
nodeSizeMin = size;
}
}
// ノードCSVファイルからノードを作成
// ノードごとに位置、ラベル、サイズを設定
for (int i = 0; i < nodesRowCount; i++) {
TableRow row = nodesTable.getRow(i);
String label = row.getString("word");
float size = row.getFloat("size");
float x = random(width); // ノードの初期位置をランダムに設定
float y = random(height);
nodes[i] = new Node(x, y, label, size);
}
// edgeWeightMaxとedgeWeightMinを極端な値で初期化
edgeWeightMax = Float.MIN_VALUE;
edgeWeightMin = Float.MAX_VALUE;
// エッジCSVファイルからエッジを作成
// エッジごとにノード間のリンクを設定
int edgeIndex = 0;
for (int i = 0; i < edgesRowCount; i++) {
TableRow row = edgesTable.getRow(i);
String labelA = row.getString("word1");
String labelB = row.getString("word2");
float weight = row.getFloat("weight");
Node a = findNodeByLabel(labelA);
Node b = findNodeByLabel(labelB);
if (a != null && b != null && a != b) {
edges[edgeIndex++] = new Edge(a, b, weight);
// edgeWeightMaxとedgeWeightMinを更新
// エッジの重みの最大値と最小値を更新する
if (weight > edgeWeightMax) {
edgeWeightMax = weight;
}
if (weight < edgeWeightMin) {
edgeWeightMin = weight;
}
}
}
}
void draw() {
background(255); // 背景を白にリセット
// エッジを更新および描画
for (Edge e : edges) {
if (e != null) {
e.update(); // エッジの引力を更新
e.display(); // エッジを描画
}
}
// ノードを更新および描画
for (Node n : nodes) {
n.update(); // ノードの位置を更新
n.display(); // ノードを描画
}
}
void mousePressed() {
// マウスでノードをクリックしたときに選択する
for (Node n : nodes) {
if (dist(mouseX, mouseY, n.position.x, n.position.y) < n.radius) {
selectedNode = n;
break;
}
}
}
void mouseDragged() {
// ノードが選択されている場合、そのノードをドラッグで移動
if (selectedNode != null) {
selectedNode.position.set(mouseX, mouseY);
}
}
void mouseReleased() {
// マウスを離したときにノードの選択を解除
selectedNode = null;
}
Node findNodeByLabel(String label) {
// ラベルを使ってノードを検索する
for (Node n : nodes) {
if (n.label.equals(label)) {
return n;
}
}
return null;
}
class Node {
PVector position; // ノードの位置
PVector velocity; // ノードの速度
float radius; // ノードの半径
float size; // ノードのサイズ(元データから取得)
String label; // ノードのラベル
Node(float x, float y, String label, float size) {
position = new PVector(x, y);
velocity = new PVector(0, 0);
this.label = label;
this.size = size;
// ノードのサイズを半径にマッピング
this.radius = map(size, nodeSizeMin, nodeSizeMax, nodeRadiusMin, nodeRadiusMax);
}
void update() {
// シンプルな力を適用して力レイアウトを実現
for (Node other : nodes) {
if (other != this && selectedNode != this) {
// 他のノードとの方向を計算
PVector dir = PVector.sub(position, other.position);
float distance = max(dir.mag(), 5); // 距離が小さすぎないように最低値を設定
dir.normalize();
// 斥力の計算(距離の2乗に反比例)
float force = repulsionForceConstant / (distance * distance);
dir.mult(force);
velocity.add(dir);
}
}
// ウィンドウ中心に向かう力を適用(フックの法則によるバネの力)
PVector center = new PVector(width / 2, height / 2);
PVector toCenter = PVector.sub(center, position);
toCenter.mult(springConstant);
velocity.add(toCenter);
// 速度を制限(あまり速くなりすぎないように)
velocity.limit(5);
// 選択されていない場合に位置を更新
if (selectedNode != this) {
position.add(velocity);
}
// 速度を減衰させる(摩擦のような効果)
velocity.mult(0.9);
// ノードをウィンドウ内に保持(ウィンドウの境界を超えないように)
position.x = constrain(position.x, radius, width - radius);
position.y = constrain(position.y, radius, height - radius);
}
void display() {
// ノードを描画
fill(100, 150, 250); // ノードの色を設定
noStroke();
ellipse(position.x, position.y, radius * 2, radius * 2); // ノードを円として描画
fill(0);
textAlign(CENTER, CENTER);
text(label, position.x, position.y); // ノードのラベルを表示
}
}
class Edge {
Node a; // エッジの一方のノード
Node b; // エッジのもう一方のノード
float weight; // エッジの重み
Edge(Node a, Node b, float weight) {
this.a = a;
this.b = b;
this.weight = weight;
}
void update() {
// 接続されたノード間に引力を適用
PVector dir = PVector.sub(b.position, a.position);
float distance = max(dir.mag(), 5); // 距離が小さすぎないように最低値を設定
float force = attractionForceConstant * (distance - 100); // 引力の強さを計算
dir.normalize();
dir.mult(force);
a.velocity.add(dir); // ノードaに引力を加える
b.velocity.sub(dir); // ノードbに反対方向の力を加える
}
void display() {
// エッジを描画
stroke(0); // 線の色を設定
// エッジの重みに基づいて線の太さを設定
float strokeW = map(weight, edgeWeightMin, edgeWeightMax, edgeStrokeWeightMin, edgeStrokeWeightMax);
strokeWeight(strokeW);
line(a.position.x, a.position.y, b.position.x, b.position.y); // エッジを線として描画
}
}
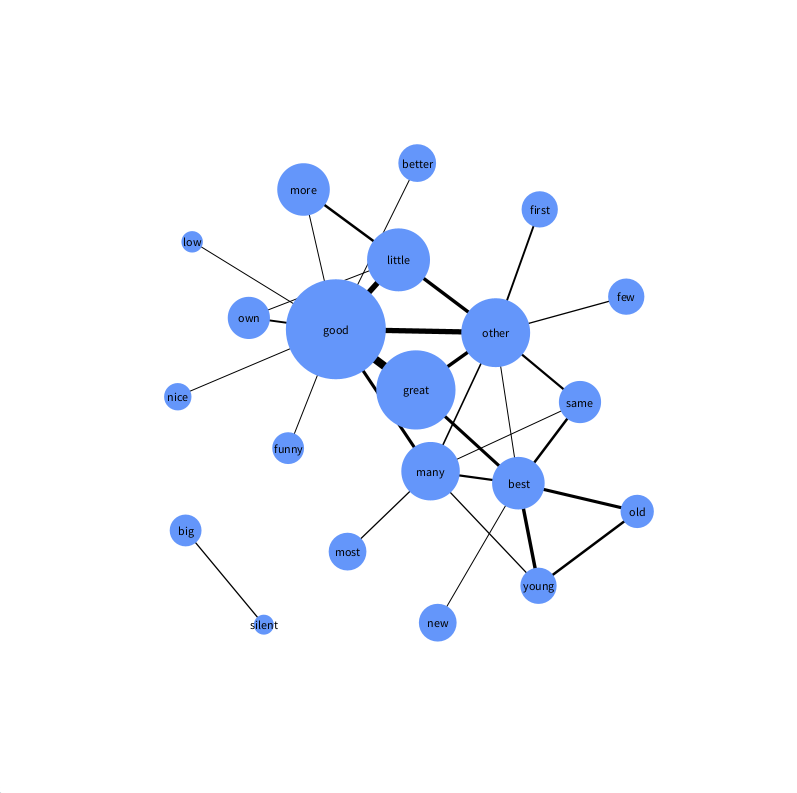
結果
今回のデータでは「good」や「great」が共起的によく使用されていることが可視化されました。
まとめ
今回は「共起ネットワーク」を題材にして、ネットワークを可視化するためにはどのようなデータが必要か、力学モデルを使った可視化はどのようにプログラムするかについて解説しました。ネットワーク分析は、データサイエンスの中では比較的よく使われ、日常生活に近いテーマにも馴染むものです。ネットワークの可視化は、pythonのライブラリ(matplotlib,plotly等)や、Cytoscape Gephiといった可視化に特化した優れたツールが多いのも事実です。
しかし、Processingで実装してみることで、ジェネラティブアートなどで馴染み深い物理シミュレーションと融合させたりカスタマイズを加えることで、アーティスティックな表現への展望も開けてくると思います。ぜひ、挑戦してみてください。